不稳定导热过程中,温度T与时间τ、空间坐标(x、y、z)的关系可用傅立叶导热微分方程来描述,即:
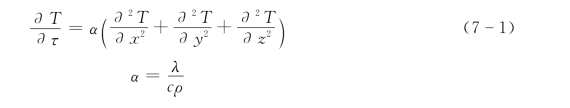
式中 α——热扩散率;
λ——热导率;
c——比热容;
ρ——密度。
式(7-1)是根据热量传递规律与能量守恒定律导出的,它适用于无内热源固体导热,也适用于静止的(无对流)液体的导热。式(7-1)的解为通解。为解某一具体问题,必须给出此问题的定解条件,包括初始条件和边界条件,才能求得具体问题的特解(定解)。在有些专门论述热量传输的著作中,把定解条件分成单值条件,单值条件包括:①几何条件(物体的形状,大小等);②物理条件(c、ρ、λ等及其和温度的关系);③时间(初始)条件τ=0时物体内各点的温度;④边界条件。
在不稳定导热情况下,导热微分方程的解具有非常复杂的形式。目前只能用来解决一些形状最简单(如平板、圆柱、球)的物体的不稳定导热问题。
下面以半无限大铸件在半无限大铸型中的冷却过程为例,运用导热微分方程求铸件和铸型的温度场。
假设:①铸件与铸型的接触面为平面;②铸件和铸型的材料都是均质的,其热扩散率近似地认为是不随温度而变的定值;③铸型的初始温度为T 20;④液态金属充满型腔后即停止流动,且各处温度均匀,即铸件的初始温度为T 10。
将坐标原点设在铸件与铸型的接触平面处。在这种情况下,铸件和铸型任意一点的温度t与y及z无关,是一维不稳定导热问题。式(7-1)变为:(https://www.xing528.com)

误差函数的性质是:

表7-2列出铸铁和铸型的热物理参数,供计算时选用。
对于铸件,将边界条件:x=0处,T 1=T i是铸件与铸型接触界面的温度;x=∞处,T=T 1∞,代入式(7-3),可求得铸件温度场。求得铸件—铸型温度场的示例如图7-1。
表7-1 误差函数
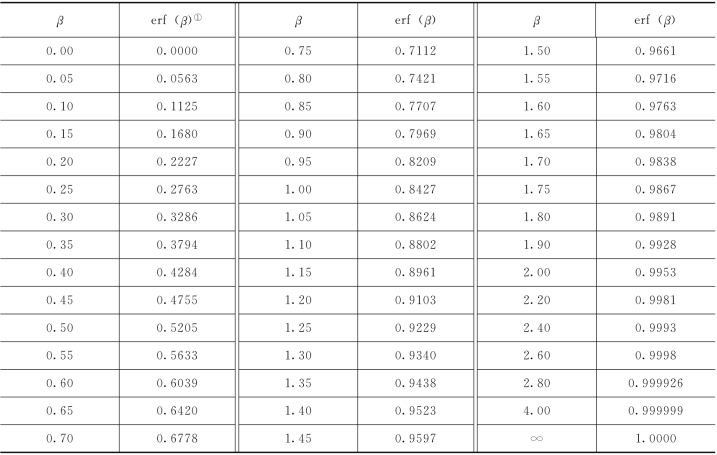
① erf(-β)=-erf(β)。
表7-2 铸铁和铸型的热物理参数

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




