纳米晶体材料力学性能预测模拟

随着计算机模拟技术的发展和人们对微纳尺度力学认识的深化，纳米结构材料力学性能计算机模拟研究已涉及力学性能的各个方面，如纳米材料的弹性模量、拉伸行为、超塑性等性能，此方面的研究是计算机模拟技术应用比较活跃的领域，计算机模拟、实验和理论研究均证实纳米材料的力学性能偏离经典力学规律。

对纳米材料结构和性能的计算机模拟一般由两部分组成：即材料自身的模型化和对实验观察到的物理性质及有代表性的特征进行模拟计算。材料自身的模型结构要受两个因素制约，即结构应尽量接近实验观察到的形态和受到计算机内存与计算时间的限制。对纳米材料的结构和性能的计算机模拟的计算模型包括连续体模型和原子级模型。连续体模型就是把材料看作连续的介质，采用的方法大多是基于纳米材料微观结构的有限元方法，它的研究对象是有限小的单元。原子级模型是把材料看作由许多单个原子的聚集体，所采用的原子级模拟方法有分子动力学方法、蒙特卡罗方法和晶格动力学方法，而它的研究对象则是单个原子。纳米材料的各个宏观量则由所有原子的统计量给出。

纳米材料细观力学的研究常常采用分子动力学方法、基于微观结构的有限元方法以及针对复杂问题时基于各种模拟方法优点混合而成的方法^{[27，96-100]}。邸玉贤等^[101]采用分子动力学模拟研究了纳米Fe，其弹性模量减少了30%或更小，随着晶粒尺寸的减小，纳米晶体的弹性模量明显地降低。Zhao等^[102]与胡慧芳等^[103]采用紧束模型分别模拟研究了纳米Ni，Ag的弹性模量也发现有所下降，模拟结果和实验结果是一致的。Cao等^[104]及梁海戈等^[105]分别利用分子动力学和嵌入原子势模拟纳米Cu在拉伸时的位错移动过程和形变过程，不同边界约束对铜单晶的内部原子运动和整体力学行为有明显影响，纳米铜线、纳米铜薄膜良好的延性主要来源于位错运动，纳米铜块体的破坏源于内部孔洞的发展。Schiøtz^[106]采用分子动力学模拟纳米Cu拉伸过程，发现随着晶粒尺寸的减小，屈服应力降低，即应力与晶粒尺寸呈现负的Hall-Petch关系。Zhao^[102]模拟研究了纳米Ni的塑性变形，发现在低温下拉伸应力达到5GPa时，纳米Ni样品产生400%的超塑性变形而没有断裂，是传统粗晶的8倍，纳米Ni具有优良的超塑性，且模拟结果与实验数据相当吻合。Froseth等^[107]用分子动力学方法描述了纳米铝晶界处单个不全位错的发射。使用Hirth和Lothe方程^[108]，他们计算了沿^[110]晶向螺形位错的不全位错间隔，即

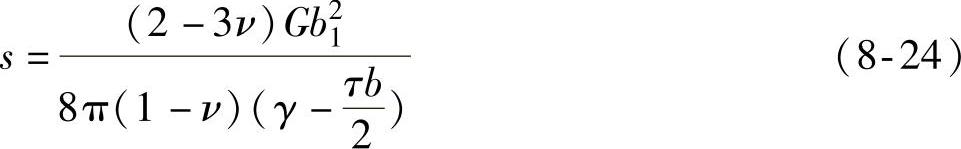
式中，b₁是不全位错的Burgers向量；γ为剪切应变；b为全位错的Burgers向量；G为剪切模量；ν为泊松比；τ为外加剪切应力。

可以看到位错间距与施加的应力有关。对于刃型位错，位错间距与应力无关

对于螺型位错，当

位错间距趋向无穷大。图8-16是Froseth等人对纳米铝进行MD模拟的结果^[107]。已知铝的堆垛层错能约为150mJ/m²，临界应力约为1.7GPa。所施加的应力为1.6GPa，且铝的晶粒大小为12nm。在图8-16a中一个不全位错已经从晶粒的左下角发射出来。第二个不全位错在图8-16b中发射并且深色的原子代表有缺陷的区域。在图8-16c中，这些不全位错穿过了晶粒，且最终被上晶粒边界吸收，如图8-16d～8-16f所示。Froseth等人还讨论了不全位错的间距及其沿位错线的不均匀分布特性。(www.xing528.com)

图8-16 不全位错形成及其扩展的MD顺序显示其中移动的位错重新构成了完整的晶格点阵，红色原子处于位错之间

a）从晶粒左下角发射出来的不全位错 b）在缺陷处发射出来的另一个不全位错 c）～f）穿过晶粒且最终被上晶粒边界吸收的不全位错

此外，Prabu等^[32]使用基于微观结构的二维有限元分析方法，研究了不同SiC颗粒分布增强Al基复合材料的应力—应变行为及失效机理，计算了该复合材料的宏观响应和局部应力/应变场，并与颗粒随机均匀分布复合材料进行了比较。结果表明，聚集态颗粒增强复合材料更容易发生界面脱粘和颗粒断裂失效，而颗粒随机均匀分布复合材料则主要由于基体的塑性流动而失效。Trebin^[109]通过分子动力学+有限元的方法模拟了原子尺度上的裂纹扩展行为。Abraham等^[110]结合从头算法，提出宏观/原子/从头分子动力学方法，利用24个并行处理器对脆性断裂进行了更为精细的紧束模型+分子动力学+有限元模拟。近几年人们又提出了几种分子动力学之间的混合，比较典型的是Shimojo等^[111]提出的可升级分子动力学算法。Kumar^[112]认为可以通过在分子动力学中引入其他理论方法，诸如团簇变分法以及动力学矩阵法等解决现代分子动力学计算效率的问题。

Tadmor等人提出了一种混合模型方法^[113，114]，模型中核心部分的临界行为由MD（分子动力学方法）模拟实现，而该核心部分由有限元建立的材料模型围绕。实际上，该方法是MD和FEM的混合方法（准连续介质方法——Quasicon-tinuum Method）。图8-17a显示了如何用上述QC法揭示晶界位错的产生^[115]。Sansoz和Molinari^[115]模拟了一个承受剪力的Σ9重位点阵晶界（CSL Sigma=9）。他们通过原子的重排，降低沿晶界发生塑性变形的剪切应力，即从5.5GPa降到1.5GPa。图8-17b显示了Ⅰ、Ⅱ、Ⅲ三个阶段中原子的相应位置^[115]。Σ9重位点阵晶界呈水平且通过模型中心，占据完整面心立方FCC点阵位置的原子呈深色，而晶界处及堆垛层错处的原子呈浅色。在第Ⅰ阶段中，因为应力低于5.5GPa，没有发生原子重排现象。在第Ⅱ阶段中，由增加的浅色原子数量，可以看到原子的活动性增加，在晶界发生了重排。第Ⅲ阶段显示了堆垛层错从晶界到晶内的发射。

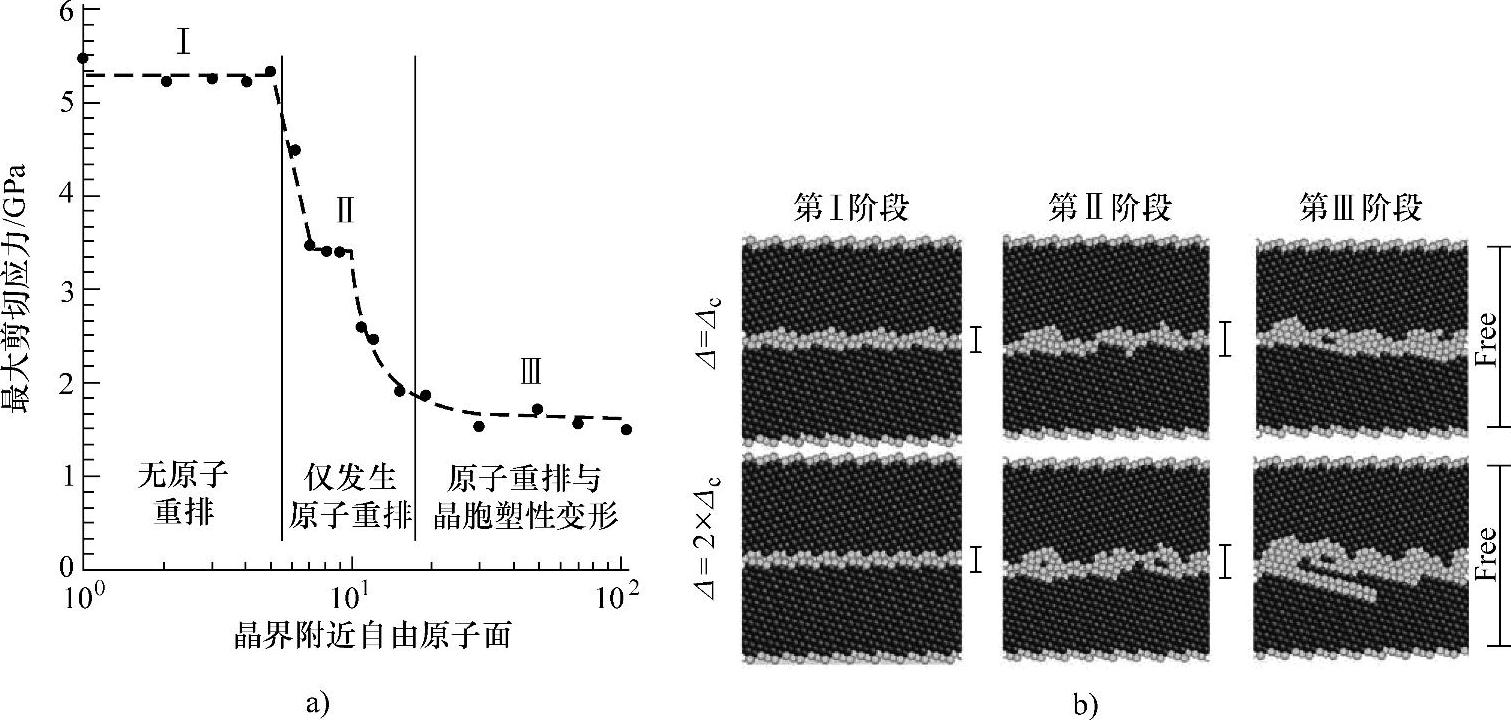
图8-17 沿铜中Σ9重位点阵晶界剪切的准连续介质模拟

a）在不同阶段（从Ⅰ到Ⅲ）中，可自由移动的原子层数增加 b）三个阶段在两个不同位移水平（Δ_c和2Δ_c，Δ_c表示最大应力处的临界位移）条件下的晶界活性（浅色原子表示）

尽管目前基于纳米晶体材料微结构的力学性能预测还鲜有报道，但上述纳米晶体材料制备热动力学参数对纳米晶粒尺寸大小与分布的影响以及纳米晶体材料力学性能的模拟研究，为高性能纳米晶体材料的可控制备及其纳米力学行为研究提供了重要的理论基础。在此基础上，通过结合纳米晶材料制备实验过程中热动力学工艺参数的控制，达到纳米晶材料力学性能可控的目的。今后的研究尚需注意以下几个问题：第一，由于研究纳米材料尤其是纳米复合材料细观力学问题的复杂性，仅用一种模拟方法有时在解决问题时会遇到各种各样的困难，因此，不同的研究层次需要采取不同的研究方法。第二，目前纳米材料研究中各层次的联系还不够紧密，各层次之间还缺乏系统的研究，还找不到一个由微观参数到宏观性能指标的定量的科学准则来指导材料设计。所以，如何发展一种新型的多尺度模拟方法，使不同模拟层次相耦合，建立计算机模拟的统一模型，成为纳米材料设计发展的关键^[116]。第三，应该进一步加强纳米材料实验和基础强化理论的研究，以使纳米科技更好地应用于工程实际。