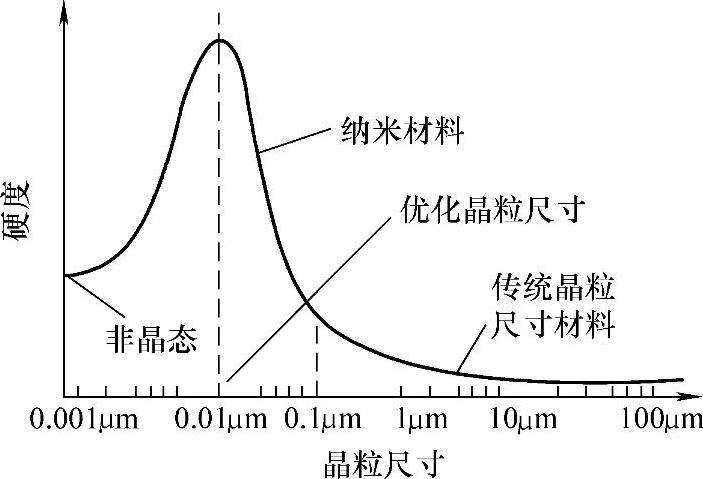
图8-13 材料硬度随晶粒尺寸的变化
注：当晶粒尺寸大于优化值时，随着晶粒尺寸的增加，硬度增加（Hall-Petch关系）。当晶粒尺寸小于优化值时，随着晶粒尺寸的减小，硬度减小（反Hall-Petch关系）[54]。
在传统块状材料中，细化晶粒尺寸可以提高硬度，这一点对于薄膜或涂层也是同样的。随着晶粒尺寸的减小，位错的繁殖和活动性受到限制，根据Hall-Petch关系[51，52]，材料硬度随着晶粒尺寸的减小而增加。当晶粒尺寸下降到几十纳米时，这种效应尤其显著。但当晶粒尺寸小于10nm时，决定着传统材料硬度的位错运动对于纳米材料的硬度有着较小的影响。在这种小尺度条件下，由于晶界滑移[53]，晶粒尺寸的进一步减小将引起硬度的降低（图8-13）。由晶界滑移引起的软化主要归因于晶界上存在的大量缺陷，这些缺陷允许原子和空位在应力作用下发生快速地扩散[54，55]。同样，硬度的进一步增加需要抑制晶界滑移，而晶界滑移的抑制可以通过设计合适的微观组织，如通过增加晶界强度和晶界微结构复杂性来实现[56]。一般认为多相组织结构具有高内聚强度界面，这是因为不同晶相常表现出不同的滑移体系，且提供复杂的晶界以调节共格应变，从而阻止了空隙或裂纹的形成[57]。大量的硬质材料可用于纳米复合涂层微观组织设计中，图8-14显示了潜在的硬质涂层材料。
除了硬度之外，优良的力学性能还包括高韧性。纳米复合薄膜高韧性的获得可以通过纳米尺度晶粒结构以及纳米尺度裂纹的变形、扩展及终止获得[59]。Vepˇrek提出了一种高韧性新型超硬陶瓷/陶瓷纳米复合涂层的设计思想[60-62]。在这种设计思想中，为了避免晶界滑移，常使用多相结构获得复杂的界面微结构，且为了获得强结合界面常使用具有强烈形成二元化合物倾向的三元或四元体系[53]。晶粒尺寸常被控制在3～4nm，而晶粒之间的距离常保持在小于1nm。基于这种设计思想，
与其合作研究者们采用等离子体化学气相沉积法制备了纳米结构TiN/非晶态Si3N4/非晶态和纳米结构TiSi2纳米复合材料（nc-TiN/a-Si3N4/a-&nc-TiSi2）[63]，纳米结构TiN/非晶态Si3N4（nc-TiN/a-Si3N4）[64]，纳米结构W2N/非晶态Si3N4（nc-W2N/a-Si3N4）[65]，纳米结构VN/非晶态Si3N4（nc-VN/a-Si3N4）[66]，纳米结构TiN/非晶态BN（nc-TiN/a-BN）[67]以及纳米结构TiN/非晶态BN/非晶态TiB2（nc-TiN/a-BN/a-TiB2）[68]超硬纳米复合涂层。在nc-TiN/a-Si3N4/a-TiSi2和nc-TiN/a-Si3N4/nc-TiSi2纳米复合涂层体系中，TiN纳米晶体嵌入到处于晶界的非晶Si3 N4中，非晶TiSi2和微晶TiSi2也处于晶界中（图8-15）。具有这样微结构的复合涂层体系具有极高的硬度，维氏硬度超过100GPa[63]。此外，压痕试验中没有出现微裂纹，表明该涂层具有良好的韧性。这是因为纳米尺度的晶体中，裂纹尖端不存在较大的应力集中，而在裂纹尖端的应力集中系数可通过下式估计[69]，即
式中，c是裂纹长度；r为裂纹尖端半径。
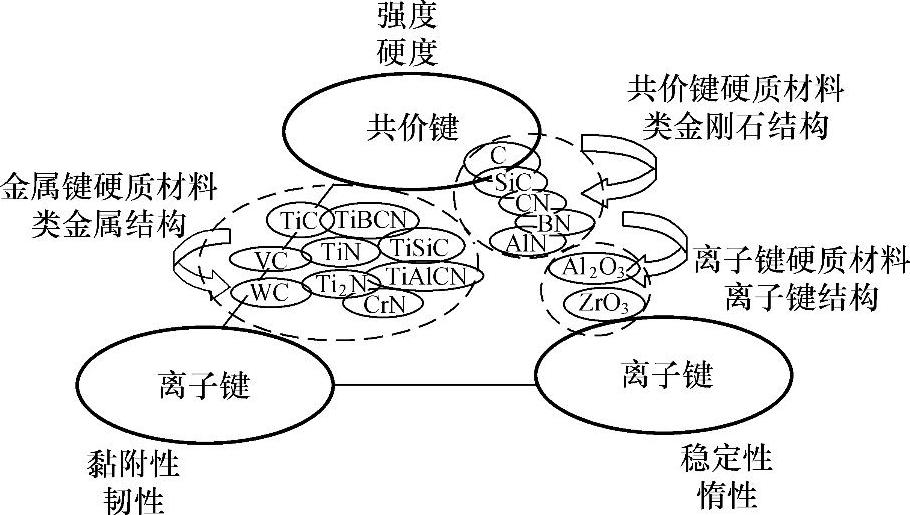
图8-14 化学键三角形中的硬质纳米复合涂层材料及其性能随着化学键的变化
注：这些材料包括——具有高硬度和高温强度的共价键结合材料，具有优良结合强度和韧性的金属键结合材料，以及具有良好稳定性和化学惰性的离子键结合材料。[58]
对于c/2=1～2nm和r=0.2～0.3nm（1个原子的键长），根据公式8-11计算的应力集中系数很小，其值只有4～6，而在传统的微观结构中，应力集中系数可达30～100[63]。在纳米复合材料结构中，由于尺度为3～6nm的微晶中没有位错，裂纹扩展也受到强烈地抑制。在这种情况下，裂纹扩展只能沿着晶界进行。当裂纹尺寸接近微晶的大小时，裂纹或发生弯曲或产生分支。在此之后，只有外加应力垂直于弯曲平面或分支裂纹的应力分量才可能导致裂纹的进一步扩展。因此，使裂纹扩展的应力减小，裂纹扩展速率降低。在
的纳米复合材料微观结构设计中，两种互不相溶的氮化物（nc-TiN和a-Si3N）用于提高热稳定性[70，71]，但这可能会降低晶粒和晶界之间的界面黏结强度[72]。当裂纹尖端的局部拉应力足够高时，就会导致不稳定的裂纹扩展[73]。
图8-15 nc-TiN/a-Si3N4/a-及nc-TiSi2纳米复合结构示意图
注：TiN纳米晶体嵌入在处于晶界的非晶氮化硅中，非晶TiSi2和微晶TiSi2也处于晶界中。TiN晶粒尺寸约为3～4nm，TiN晶粒间距小于1nm[63]。
为了获得超硬纳米涂层，通常避免发生强烈的塑性变形、位错运动和晶界滑移，从而可能使延展性降低。为了改善纳米复合涂层的韧性，越来越多的研究者认为，一定程度的晶界滑移是必要的。通常情况下，要克服陶瓷块体材料的脆性，一般需要加入另外一种延性相以改善复合材料的韧性[74-76]。近年来，通过添加纳米尺度的金属微粒[77，78]，这些陶瓷复合材料的微观结构得到了进一步的细化，这种情况也同样适用于薄膜和涂层材料。Musil及其合作者在金属Cu[79，80]，Ni[81-83]和Y[84]中嵌入氮化物陶瓷晶体，在这些涂层中的陶瓷相晶粒尺寸通常被控制在小于10nm的范围，且晶界体积远远大于硬质相体积[85]，这些涂层体系的硬度可在35～60GPa之间变化。金属基体的存在，可以使裂纹尖端钝化，并通过自身的塑性变形改善韧性。但在这样的复合结构设计中，金属晶界的厚度不能太薄：因为在纳米尺度颗粒的情况下，位错运动受到限制[86]，因而非常薄的晶界导致增韧机制失效。一旦出现这种情况，陶瓷/金属纳米复合材料与陶瓷/陶瓷纳米复合材料的力学响应将非常相似，而这有悖于添加纳米尺度的软金属微粒改善韧性的目的。另一种提高韧性的方法是允许晶界滑移，以释放累积的应变。Voevodin等[86，87]在无定形碳（a-C）基体中嵌入10～20nm的硬质碳化物晶粒，该量级的晶粒能够限制初始裂纹尺寸且能形成大量的晶界[88]。非晶边界的厚度应保持在2～10nm之间，这样既可以防止相邻晶粒原子面的相互作用，并促进晶界滑移，又可以限制直裂纹路径的形成。作为结果，nc-TiC/a-C和nc-WC/a-C纳米复合薄膜以较少的硬度损失获得了较高的“抗剥离韧性”[89]，其值为纳米晶硬质合金的4～5倍。
如上所述，纳米材料的结构一般是由晶粒、非晶和准晶等颗粒主元和界面主元构成的，对其结构分析主要是描述纳米晶相结构、界面结构及其缺陷种类和数量等[90]。目前常通过以下途径实现：利用欧几里得几何体视学，可以获得材料规则状态的微观结构、平均颗粒直径及其分布状态的统计信息[91]；而对于不规则的几何特征组元，如晶界、位错等，则需采用分形几何来描述，并结合计算机图形学显示纳米材料的微观结构特征。分布函数理论是从统计的角度描述材料结构的理论，限于计算数学的水平，只有描述双粒子位形的径向分布函数理论应用比较广泛[92]。对分析技术是用原子对成键关系及其周围共有原子间的成键关系描述材料结构的一种方法，常采用四个参数（ijmn）键对描述原子局域结构[93]。
纳米材料的计算机模拟基于原子论模型，把纳米材料看作许多单个原子的聚集体，并且每个原子都作为独立的研究单元，然后应用经典力学或统计力学描述单个原子的规律，利用固体理论预测纳米材料的结构和性能。目前常采用的有分子动力学方法和蒙特卡罗及多尺度计算设计等方法。其中，基于宏观、细观、微观力学的多尺度计算设计方法，能够定量描述纳米复合材料细观结构对宏观性能的影响，为控制复合材料中界面条件、增强相的几何参量及其分布提供可靠依据[94]。但是，有关该方法的研究仍需进一步完善，如细观力学还不能解决复合损伤强度相关的协同效应，非比例加载响应和有棱角增强相的细观结构等问题。
2.纳米材料微结构变化动力学模拟
针对纳米材料的结晶动力学过程，这里主要介绍纳米材料从非晶态到晶态的整个晶化过程中晶粒从成核到长大各个生长阶段的微结构变化的动力学，以及一种纳米晶体材料微结构定量计算模型，根据该模型可以计算出各生长阶段晶粒尺寸和纳米材料的晶粒密度[95]。
在材料从非晶态到晶态的转变的过程中，认为晶粒从临界核形成到长大成完整的纳米颗粒分为3步：第一步，晶粒生长主要由晶核界面控制。第二步，当晶粒达到半径RT以后，晶粒生长主要由溶质扩散控制。但此时晶粒之间还未接触而发生交叠，称为溶质扩散的硬冲击过程。第三步，晶粒继续长大，当晶粒相互接触后，此时界面溶质浓度降低，溶质扩散过程由硬冲击变为软冲击过程。因此，当临界核形成后，晶粒生长首先主要由晶核界面控制，溶质在临界核的界面上自由堆积，直到界面溶质达到C∗，在此阶段，晶粒半径随时间的变化可由公式（8-12）表示
r1=r∗+u（T）（t1-τ） r≤RT （8-12）
式中，τ是临界核形成的时间；u（T）是界面控制的生长速率；r∗是临界核半径；t1为晶粒半径生长为RT时对应的时间。
当晶粒半径达到RT以后，晶粒生长主要由扩散控制，此时半径的变化由公式（8-13）给出，即
(www.xing528.com)
式中，D（T）是阿列纽斯型慢扩散温度依赖扩散系数；Cxt是晶粒内的溶质浓度；C∗是晶界的溶质浓度；C0是晶粒外远距离处非晶态的溶质浓度。
如果定义有效扩散系数D0（T）为
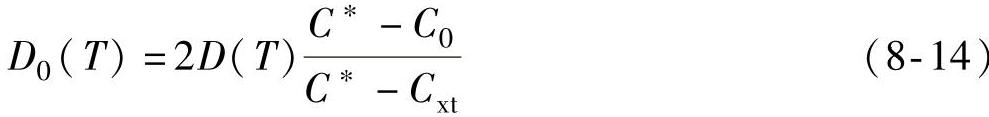
可以得到此时晶粒半径随时间变化公式
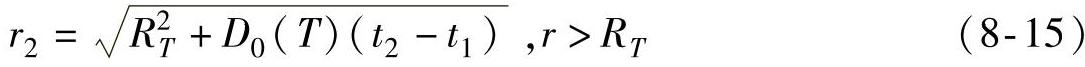
晶粒半径继续长大到晶粒之间相互接触以后，在晶粒边界，溶质浓度梯度下降，此时溶质的扩散由硬冲击变为软冲击，软冲击的结果将导致晶粒外远距离处溶质浓度C0的增加，此时C∗将换成随时间变化的C（t）。
γX（t）Cxt+（1-γX（t））C（t）=C0 （8-16）
式中，X（t）是非晶态到晶态的体积转换分数；γ是最大体积转换分数。
此时
式（8-18）中
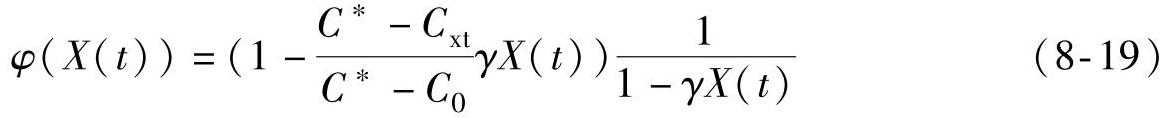
因此，最后的晶粒半径应为
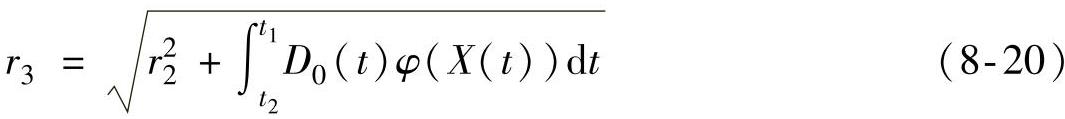
对软冲击过程，晶粒生长与体积转换分数有关，随着结晶过程的进行，逐渐变慢。由JMAK的晶体结晶动力学公式，我们得到下式
X（T，t）=1-exp（-Xext（T，t）） （8-21）
其中
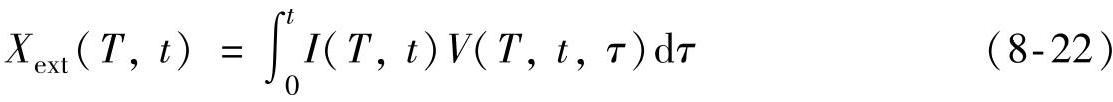
V（T，t，τ）是τ时刻形成的临界核在t时刻的体积，因此由式（8-20）、（8-21）知，根据晶粒半径可以求出转换分数X（T，t），对一定的热处理温度T，我们可以得到晶粒密度的计算公式为
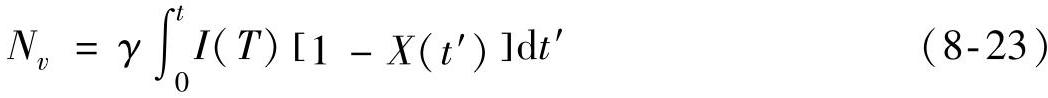
因此，从经典理论得到的实验数据估算的随时间变化动力学参数u（t），D（T），I（T），我们就可以对不同热处理情况下的晶粒尺寸和晶粒密度进行计算。
通过对纳米材料微结构设计及其结晶动力学过程的研究，不仅可以模拟纳米材料微观组织形貌，还可以分析晶粒从成核到长大的整个微结构变化过程，提出一种晶粒生长各阶段的定量计算模型，根据该模型，可以对纳米材料的晶粒尺寸和密度进行模拟计算，进而对纳米晶体材料力学性能进行预测和控制。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
