固体表面接触理论简介

接触力学的理论研究涉及黏弹性力学、破裂机理和表面科学等综合学科^[1-6]。接触理论所要解决的问题是当固体接触的时候，它们最初是在一个点上或一条线上的接触；在微小的载荷作用下，它们在最初的接触点附近发生变形，致使它们在一个有限的区域上接触。尽管该区域比起两物体尺寸来说可能是很小的，仍然需要一个接触理论来预测这个接触区的形状，接触区的尺寸如何随载荷的增加而增大，接触区的大小和分布，及其穿过界面的传递方式等，最终应能计算出两物体接触区附近的变形分量和应力分量。

接触力学研究的典型理论模型包括Hertz^[7]接触理论、JKR^[8]理论、DMT^[9，10]理论、M-D^[11，12]理论以及GW^[13]理论和近年来基于分形理论的Pers-son^[14-18]接触理论等。由于不同理论模型的基本假设和初始条件存在差异，不同理论的结论甚至存在冲突，致使在理论研究上存在许多争议。这些争议表明了在固体接触力学研究上还存在着理论问题没有得到圆满解决。

从Hertz接触理论开始，每一种接触理论都有其特定的理论基础和适用范围^[19]，它们之间相互补充，有时又相互矛盾，它们共同支撑着接触力学的研究和发展，形成现代接触力学的基本理论。

鉴于Hertz接触理论是接触力学的经典线弹性理论，也是弹塑性接触力学的理论基础，许多后续的理论研究成果从某种意义上讲是Hertz接触理论的扩展，因此本节主要介绍一下Hertz接触理论及其在实际接触表面上的应用模型。

1.Hertz接触理论

早在1886年，赫兹（Hertz）利用弹性理论的基本方程，提出了分析计算两个理想光滑表面的接触应力的数学模型。它以弹性固体的法向接触为基本前提，其基本假设还包括：接触表面光滑；表面间无摩擦、无黏附；接触物体的材料为均匀的、各向同性的、符合胡克定律的理想弹性体；接触区域与结构尺寸相比很小。

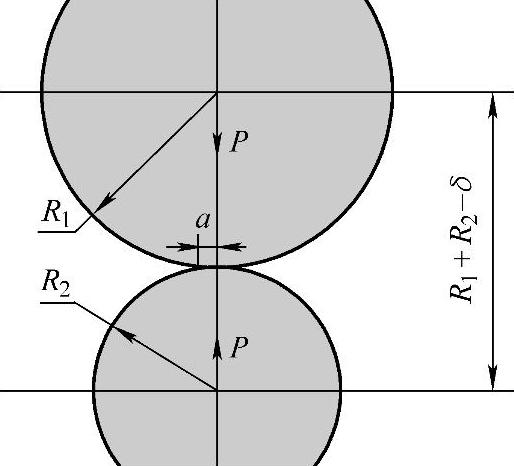
图7-1 弹性球的接触示意图

对于半径、材料弹性模量和泊松比分别为R₁和R₂、E₁和E₂、μ₁和μ₂的两个弹性球体接触时（图7-1），等效模量E^∗和等效曲率半径R分别为

E^∗=[（1-μ²₁）/E₁+（1-μ²₂）/E₂]^-1 （7-1）

R=R₁R₂/（R₁+R₂） （7-2）

若两球接触面的接触圆半径为a，向两接触球施加的接触载荷为P，则运用弹性半空间点载荷的作用原理，可求得在圆a范围内距离中心线为r的圆周一点上所承受的压力（Hertz压力）为

p=p₀{1-（r/a）²}^1/2 （7-3）

式中，p₀为接触区域内所受压力的最大值。

接触面半径a的大小反映了在载荷P的作用下两接触球体的变形程度，接触面的半径a与接触载荷P有如下关系式

a=（3PR/4E^∗）^1/3 （7-4）

按假定的前提条件a＜＜R，则远处点（相对于接触区域）的接近量为

δ=a²/R=（9P²/16RE^∗2）^1/3 （7-5）

接触区域内的最大压力值为

p₀=3P/2πa²=（6PE^∗2/π³R²）^1/3 （7-6）(www.xing528.com)

当刚性球与弹性半空间平面接触时，E∗=E₀/（1-μ₀²），式中的E₀和μ₀为弹性半空间的弹性模量和泊松比，R等于刚性球的半径。这时远处点的接近量δ所代表的是球体压入到弹性半空间中的位移量。

由于Hertz理论仅适用于a＜＜R的小变形条件下的接触问题，当刚性球与弹性半空间平面接触发生较大变形时，Sneddon^[7]解决了压头压入弹性半空间时的接触问题，当压头为刚性球时

式中，R为压头半径。

此时的接触载荷P与接触半径a的关系为

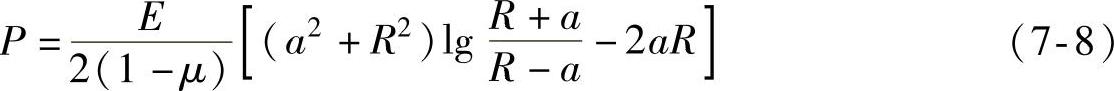
2.实际表面的接触力学^[20]

如前所述，在Hertz接触力学模型中，总是假设实际接触面积与名义接触面积的比很小，且忽视了不同接触区域之间的相互作用。但实际的零件表面与理想光滑表面明显不同，零件表面的接触也不会仅仅是弹性接触和没有法向及切向载荷的理想状态。因此，实际零件的接触无疑是一个非常复杂和困难的问题。

对于粗糙表面，微凸体之间的接触应力可写成

式中，R_P为最大凸峰高度；h_r为凸峰高度；R_P-h_r即为峰顶的变形值；β表示峰顶的当量曲率半径；E′为当量弹性模量。

因此，最大的接触应力将为

其平均接触应力将为

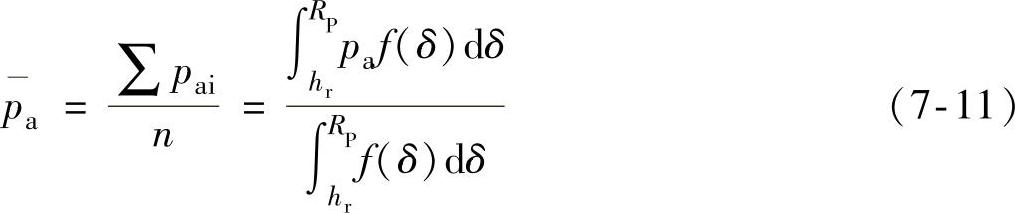
式中，n为承载微凸体的数目；f（δ）为微凸体高度的分布函数。

且有

若把两个凹凸不平的固体表面压在一起，它们之间不可能形成面接触，而只是在许多凸起的微峰间形成很多面积很小的接触点。接触点以外的区域有10nm以上的间隙，表面间的原子作用力几乎不存在，可以认为在这些区域内两个表面已被完全隔开，作用在摩擦面上的载荷全部由表面间的接触点承受。因此，实际的接触面积远小于名义接触面积，每一个微凸体上将承受更大的载荷，故其应力分布将明显高于理想光滑表面接触的情形。