纳米压痕修正及影响因素分析

1.压头/样品的接触影响

Oliver和Pharr（OP）方法只有在假设卸载时探针与压痕之间为完全弹性接触并遵循能量法则的情况下，硬度和模量值才被认为是准确可靠的。在很多情况下会因为探针尖端钝化、表面粗糙、试样不均匀使分析的条件不能满足而产生误差。在此情况下，纳米压痕试验可用于平行试验条件下较为准确的对比检测或用于其他数据分析，如参量p_max=S²在撇开接触面积的情况下，可用来衡量材料抗压痕的能力。

压痕试验中探针与薄膜之间的接触面会产生滑动摩擦，一般静摩擦力的影响随压痕深度的增加而增加，脆性材料摩擦力的影响要大于韧性材料，因此通过压痕试验检测薄膜的弹性模量时如果忽略摩擦力的影响会带来较大误差^[24]。

2.压痕尺寸效应

纳米压痕硬度值与压痕深度有很大关系，在深度较小处比在深度较大处测得的硬度值要大得多，这种现象被称作“压痕尺寸效应”。薄膜/基体的硬度是复合硬度，受薄膜、基体及其界面性质的影响。对于软薄膜/硬基体体系，按OP法确定的硬度在压痕深度很小时随深度增加，在接近基体处则受基体影响而上升，对于硬薄膜/软基体体系情况则相反^[25]。复合硬度在压痕深度极小时接近薄膜的硬度，在压痕深度很大时则接近基体的硬度。由于载荷可表示为压痕深度的函数，将薄膜/基体的总载荷p_L表示为薄膜载荷p_Lf基体分载荷p_Ls的指数形式之和^[26]，即

p_L=exp（γ_Lh）p_Lf+[1-exp（γ_Lh）]p_Ls （6-11）

式中，γ_L为负值，在深度h极小时总载荷接近薄膜载荷；h很大时则接近基体载荷。

据此通过对加卸载的载荷—深度试验数据的回归可以从薄膜/基体体系的数据中分离出薄膜和基体的力学性能。

压痕深度低于临界压痕深度时，基体对膜层硬度等力学性能的影响可以忽略，这一临界值只是膜厚的很小一部分，并随膜层与基体屈服强度之比（Y_c/Y_s）和探针尖端半径的增大而减小，压痕深度过大会产生基体效应，通常采用的是“1/10经验法则”^[27]，即压痕深度为膜层的1/10，则所测得的硬度值就非常接近真实硬度。薄膜很薄时采取分布加卸载测定膜层硬度或模量随深度的分布曲线，比较峰值大小可以定量的对比分析^[28]。

3.蠕变影响

OP数据分析法的前提是假设材料的压痕行为为完全弹性接触。在以下情况时蠕变效应会严重影响模量的测定^[29]：①材料本身为低熔点或软质材料。②卸载之前的保载时间太短。③卸载速率太慢。④载荷过大。保载期间的压痕深度随时间的延长大体符合对数蠕变方程^[30]

h=Aln（Bt+1） （6-12）

式中，h为最大载荷处的深度增加值；t为时间；A、B为拟合参数。

根据对数方程按不同的材料确定最大载荷处的保载时间，以保证相对蠕变速率值（单位时间的蠕变值与最大压痕深度之比）每分钟低于1%，这样蠕变对硬度和弹性模量检测的影响就最小。在OP法数据处理中，文献[29]提出了接触深度h_c的校正方程来减小蠕变效应对试验结果的影响

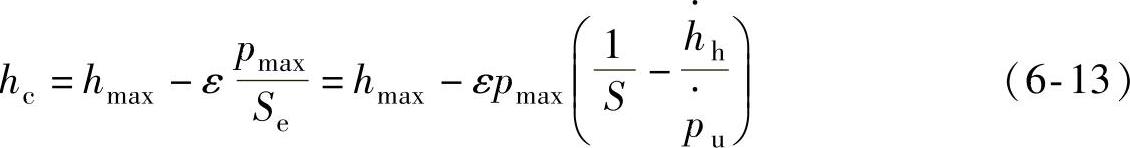
式中，S_e为校正的弹性刚度；S为卸载开始时的表观接触刚度dp/dh（p为载荷；h为压头位移）；参数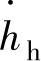为卸载前保载结束时探针位移速率，可通过检测卸载前保载过程中蠕变行为测得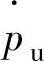；为卸载速率。

4.Oliver和Pharr经典纳米压痕力学分析方法的修正

如上所述，20世纪90年代发展起来的纳米压痕数据分析方法，并不适用于所有的情形。采用这种分析方法，在计算接触深度和接触面积时常常存在着误差。Pharr等^[31-34]使用有限元模型帮助理解和克服这种标准分析方法的弊端，该模型能够识别两种误差的来源，首先是在样品表面的残余应力带来的误差，其次是弹性恢复以后凹痕形状的改变引起的误差。

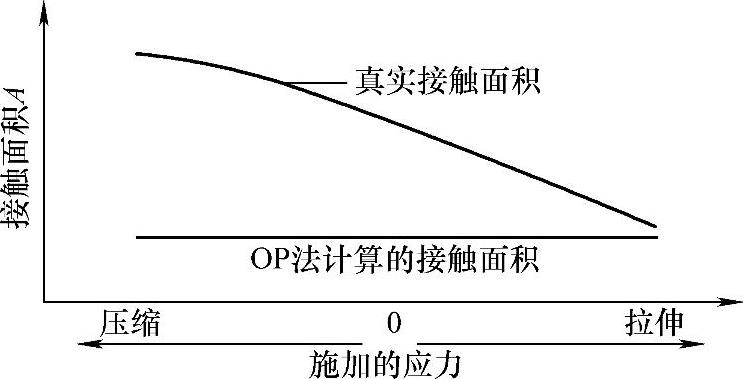
图6-7 表面处于某种应力状态时使用Oliver和Pharr法计算的接触面积与实际接触面积之间存在显著的差异

表面残余应力对压痕力学性能的影响一直是多年来讨论的主题^[35-37]，研究认为压应力能导致硬度增加而拉应力则起相反的作用。使用有限元法可以模拟纳米压头压入处于残余拉伸或残余压缩应力状态材料中的纳米压痕过程。对铝合金8009^[32]进行纳米压痕有限元模拟证明了早期的实验观察结果^[38]，即如果存在残余应力，那么通过卸载曲线计算的接触面积是不正确的。在铝合金材料有限元模型中，使用流动应力为425.6MPa的理想弹塑性金属应力应变曲线模拟该材料的力学行为，它在353.1MPa时开始屈服且产生少量的形变强化。根据Oliver和Pharr法以及使用模拟卸载曲线，有限元模型可用于直接确定接触面积。图6-7表示了接触面积随着残余应力的变化结果，可以看出，两种方法计算的接触面积的差异导致了铝合金弹性模量E和硬度H的误差^[32]。(www.xing528.com)

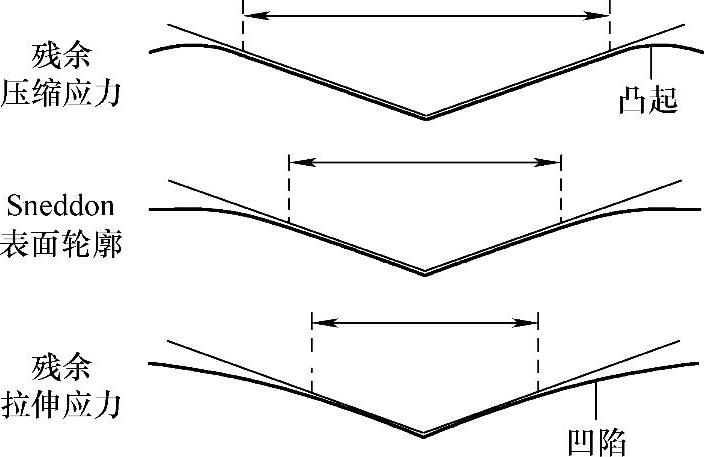
图6-8 残余应力对凸起和凹陷的影响使得Oliver和Pharr标准分析法存在误差

接触面积计算错误是由于接触边缘凸起和凹陷的错误假设导致的，如图6-8所示。在Oliver和Pharr的分析中，对样品表面几何形状的假设与Sneddon^[39]提出的弹性表面压痕分析模型中使用的几何形状是相同的。很显然，对于有较大塑性变形的材料，在使用Sneddon弹性模型时很可能会引起较大的表面几何形状偏差。事实上，接触面积误差的产生还取决于测试样品表面的几何形状与校准材料（如典型的熔融石英）表面几何形状的差异程度。即使测试样品没有残余应力，同校准材料相比，它的表面几何形状也有所不同，同时在给定深度处的接触面积也不同，这种情况经常出现在基底薄膜上^[40，41]。残余应力的存在使得使用Oliver和Pharr法计算接触面积存在较大误差的可能性增加。

凸起和凹陷问题一直是纳米压痕测试中的一个重要影响因素。然而，除了恢复压痕图像以确定真实的接触面积外，至今仍然没有一个有效的方法解决这一现象，甚至使用原子力显微镜或者电子显微镜观测压痕的边缘也是非常困难的。一个比较成功的方法^[42]就是测量E²_r/H的比值而不是单独地测量E_r和H的值。因为E_r与1/A成正比例关系，而H与1/A也成正比例关系，因此，E²_r/H应该与A无关，且不受凸起和凹陷的影响。虽然这种方法不能定量地研究力学性质，但它提供了一种确定力学性能随压痕深度变化或具有不同残余应力的相似样品之间力学性能变化的方法。

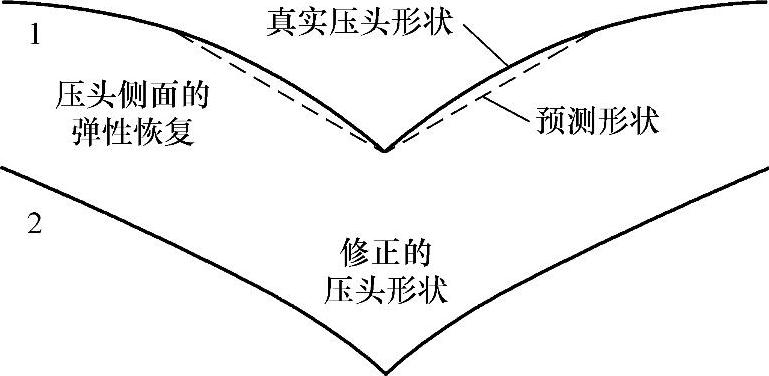
图6-9 卸载后由于压头几何形状变化引起的误差可通过使用具有微小的凹面修正的压头及引入γ项进行修正

1—实验真实压头形状与模拟预测的形状不同 2—引入一个γ项修正的压头形状

关于Oliver和Pharr分析法的另一误差是由于卸载以后纳米压痕几何形状的不正确假设而致^[33]，而这还是由于测试样品和校准材料之间存在差异的缘故。在卸载以后表现出弹性恢复的材料上的纳米压痕形状不只是一个简单的尖端形状的压痕，准确地说，纳米压痕侧面的弹性恢复将产生非常微小的凸起变形（见图6-9）。这种形状实际上取决于泊松比，所以标准的Oliver和Pharr法只有对材料的泊松比ν=0.17时才是有效的，而该值是作为标准材料的熔融石英的泊松比。

为了处理恢复的纳米压头几何形状的变化，建议在分析中使用具有微小凹面的修正的纳米压头几何形状，如图6-9所示^[33]。这需要对接触刚度S进行如前述公式（6-2）的修正。

式中，γ是压头为不同几何形状时所引入的修正系数。

对于Berkovich金刚石棱锥压头，最优修正值为

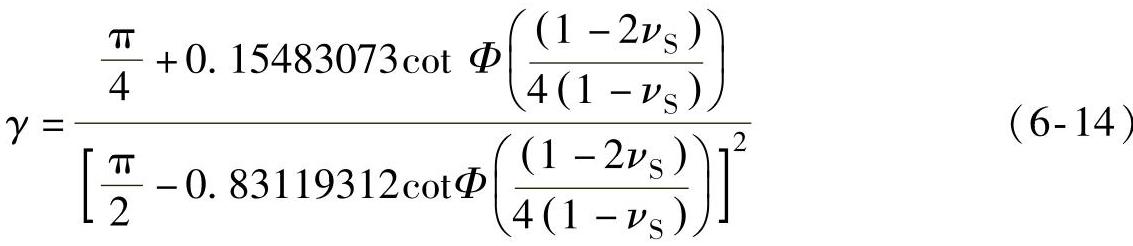
式中，Φ=70.32°。

对于立方体角锥该修正项非常大，γ由下式给出

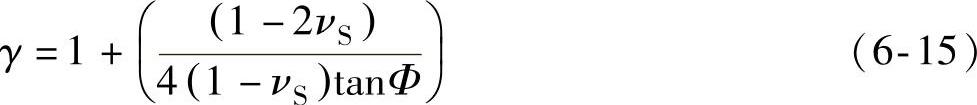
式中，Φ=42.28°。

图6-10显示了修正的接触面积如何随着真实的Berkovich金刚石棱锥压头压入深度的变化而改变^[33]。

从接触力学的观点来看，用γ修正压头几何形状的有效性还有待探讨，因为它是基于不正确的纳米压头几何形状的假设来修正纳米压痕几何学上存在的误差。然而，使用γ修正得到的E和H的值较好，且与使用标准Oliver和Pharr分析法得到的值有明显的不同。

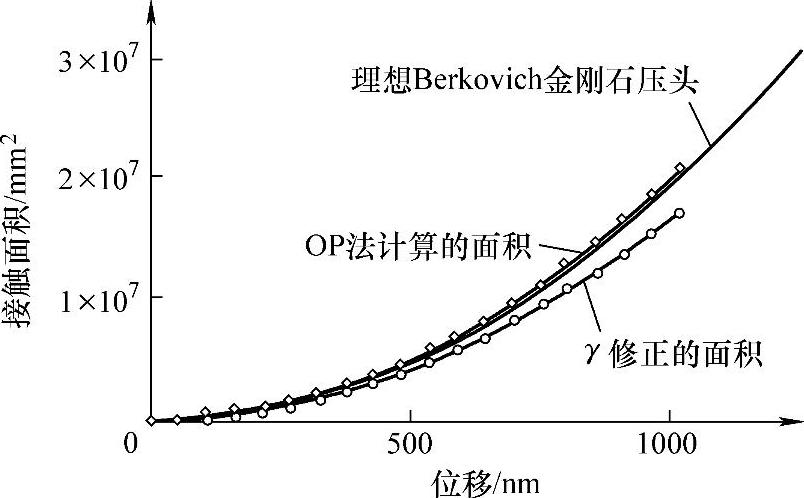
图6-10 对于真实的Berkovich压头，在给定深度下用γ修正的面积小于Oliver和Pharr法计算得到的面积