纳米压痕实验测定薄膜硬度及弹性模量的原理

纳米压痕数据分析比较典型并且被目前商业纳米试验系统广泛采用的是Oli-ver和Pharr方法（经典力学方法）^[11]，它是在经典弹性接触力学的基础上，根据试验所测得的载荷—位移曲线，从卸载曲线的斜率求出弹性模量，而硬度值则可由最大载荷和压痕的残余变形面积求得。

关于通过载荷—位移曲线所提供的数据计算样品的硬度与弹性模量，Oliver和Pharr^[12]根据Sneddon^[13]提出的不同的轴对称压头的几何外形与平整的弹性平面之间压入深度的关系，提出了一套计算方法。膜/基体系典型的纳米压痕载荷—位移曲线如图6-4所示^[12]。

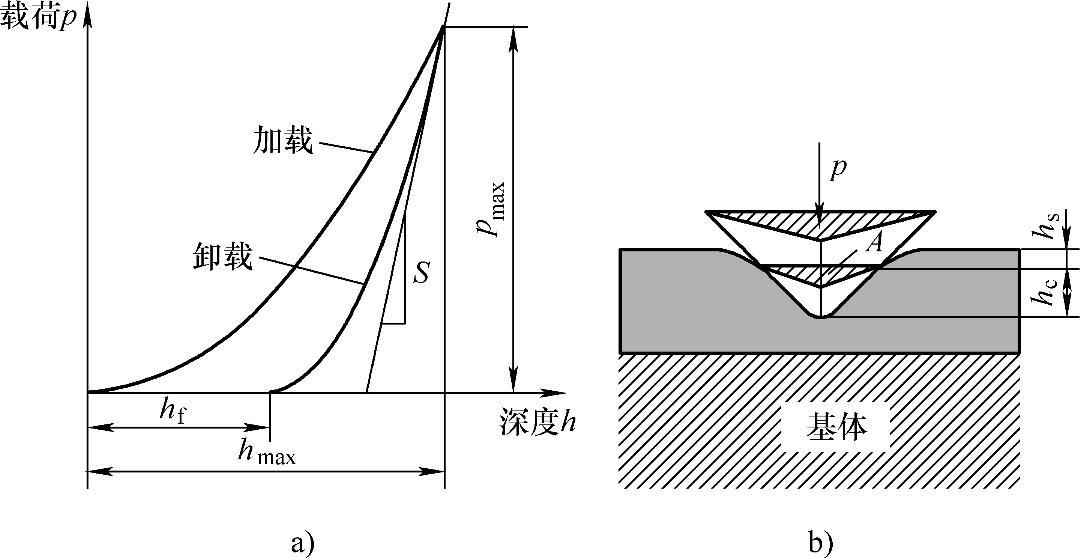
图6-4 纳米压痕试验中载荷—压入深度/位移曲线及压入膜/基体系示意图

a）载荷—压入深度/位移曲线 b）压入膜/基体系

压入深度与负载之间的关系由下式^[14]确定

p=α（h-h_f）m （6-1）

式中，p为负载；h为压入深度；h_f为卸载后残留的压痕深度；α是与几何常数、样品和压头各自的弹性模量和泊松比有关的常数；指数m与压头的几何外形有关。

最大负载点（h_max，p_max）处的斜率定义为接触刚度S，由S可以得到减缩模量E_r。S与E_r之间存在下述关系^[14]

式中，γ是当压痕为三角形或正方形时所引入的修正系数；A为压头与样品弹性接触区域的投影面积。

样品的弹性模量可以通过由式（6-2）求得的减缩模量E_r，从下式^[12]算出

式中，E和ν为样品的弹性模量和泊松比；E_i和ν_i为压头的弹性模量和泊松比。样品的硬度为^[12]

(www.xing528.com)

式中，p_max为压入过程中的最大负载；A为压痕的投影面积。

压痕面积根据在测量分析前预先通过实验确定的经验函数F进行估算^[12]

A=F（h_c） （6-5）

式中，h_c为压头与样品接触区域的垂直压入深度，它是最大压入深度h_max和压头—样品接触区域边界处样品表面压入深度h_s的差值，如图6-5所示^[14]。

h_s可以通过下式^[15]求出

式中，ε为与压头几何外形有关的常数。

通过上述的式（6-1）～（6-6），结合实验中所获得的载荷—位移曲线，就可以算出样品的硬度和弹性模量。

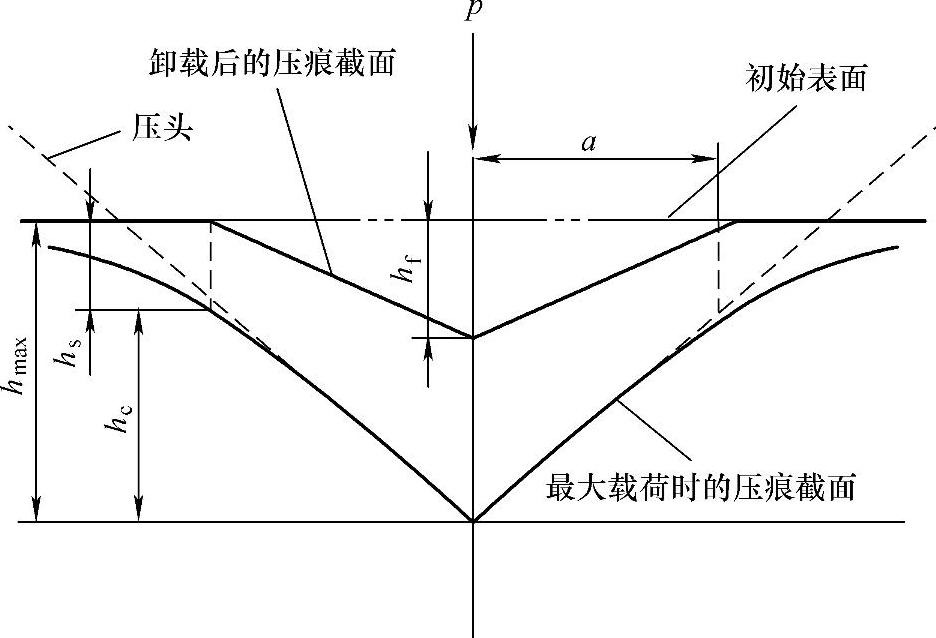
图6-5 压痕截面示意图

与通过载荷—位移曲线计算硬度、弹性模量的方法不同，通过AFM对卸载后留在样品表面的压痕进行测量，得到压痕的投影面积，根据式（6-4）也可以求出样品的硬度。通过比较两种方法测定的硬度数据，发现当压痕周围存在由被挤出压入区域的材料所形成的凸起^[14]时，这两种方法测得的硬度数据有一定的偏差，使用AFM测量的压痕投影面积计算出的硬度小于使用载荷—位移曲线上的数据计算出的硬度；而当不存在这样的凸起时，两种方法所得的硬度基本相符^[14-16]。在上述方法中，接触刚度S是通过卸载曲线确定的。连续刚度检测（CSM）做了有意义的改进，通过在驱动压针运动的直流信号上叠加一个小幅正弦信号，CSM就可以检测加载曲线任意点的接触刚度而不是像常规检测方法那样只检测卸载曲线上各点的接触刚度。这种方法的压痕深度很小，因此适合纳米薄膜的力学性能检测^[17]。弹性恢复参数ERP定义为

ERP=（h_max-hc）/h_c （6-7）

式中，ERP与硬度和模量比值H/E线性相关，表示的是材料发生弹性形变后恢复到原来状态的能力。