薄膜生长过程中的本征应力探析

薄膜的内应力主要由两部分组成，即本征应力和热应力，其中对于热应力的认识已经得到研究者的共识。薄膜内的本征应力是指不考虑薄膜生长过程中受外力及由基底与薄膜材料不同热膨胀系数所导致的热应力，仅指薄膜在生长过程中由于薄膜与基底的界面或者薄膜材料内部结构变化所产生的应力^[19]。无论薄膜以什么样的生长方式生长都包括不同的生长阶段，即从非连续的薄膜到连续薄膜的过程，因此很难用一个单一的模型来描述薄膜生长过程中的本征应力的演化。

Abermann及其合作者^[20-26]在这方面做了开创性的工作。他们的研究成果表明，薄膜内的应力的演化过程依赖于薄膜材料沉积过程中原子的迁移能力，根据原子迁移能力的高低，Abermann^[24]将应力的演化曲线分成两类，一类是高熔点材料，即材料具有低的迁移能力，薄膜内的应力随薄膜厚度的变化始终为拉应力，而对于低熔点材料，即材料具有高的迁移能力，此时薄膜内的应力值较小，并且先出现拉应力，随后为压应力。同时他们也给出了产生压应力或者拉应力的根源，他们认为此时的压应力为由与表面应力相关的Laplace压力产生的，如图4-9所示^[19]。Shull和Spaepen^[27]在研究室温沉积Cu薄膜时发现，在沉积的初始阶段薄膜内的应力为压应力，随后转变为拉应力，最后达到稳定的压应力。典型的高迁移能力的薄膜材料在生长过程中的内应力曲线示意图如图4-10^[19]所示。从图中可以看出薄膜内应力的演化规律：初始阶段为压应力，且压应力不断变化，然后产生拉应力，当拉应力达到最大值时，薄膜内应力逐渐变为压应力且应力增量近乎保持恒定。这里需要指出的是，当薄膜没有成为连续的膜之前，薄膜厚度定义为一个连续薄膜的厚度，这个连续薄膜的质量与实际的非连续膜的质量相同。Friesen和Thompson^[28]在研究Cu薄膜时发现，当薄膜的厚度小于单层厚度的1/10时，薄膜内的应力可达到1GPa，并且薄膜内的应力在沉积停止及恢复过程中可逆向变化，他们认为这种应力的可逆变化主要是由于沉积原子与表面相互作用的结果。

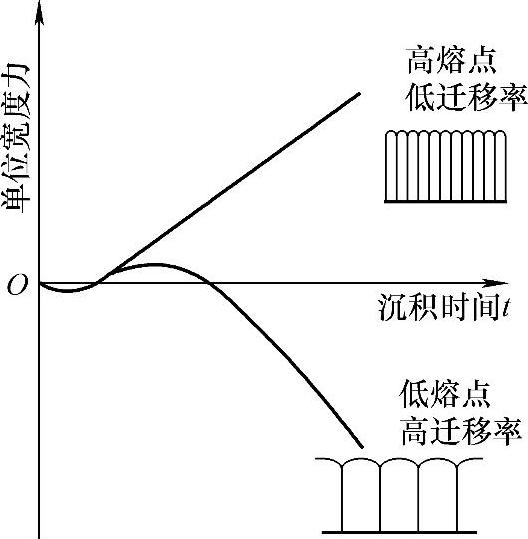
图4-9 不同薄膜内单位宽度力的典型演化曲线

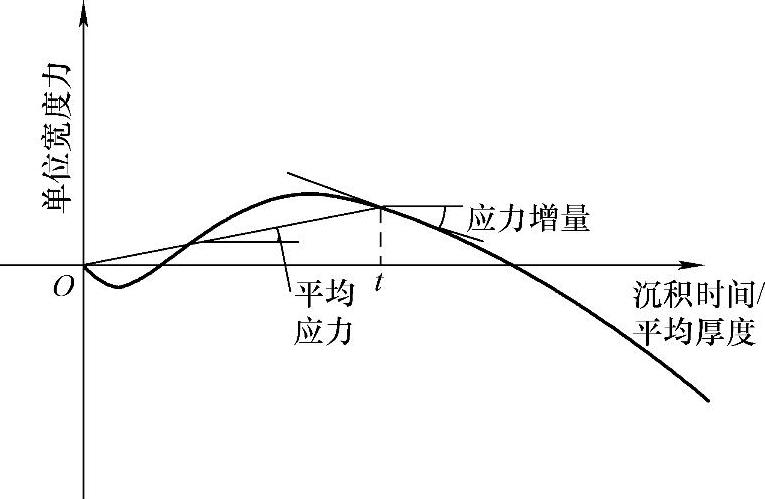
图4-10 任意时刻薄膜内的应力及应力增量

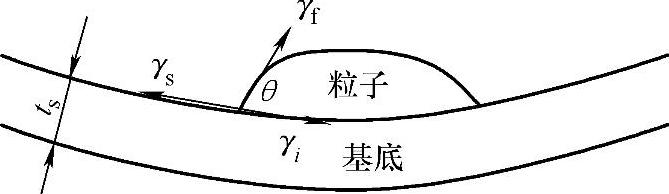
图4-11 表面及界面应力作用导致的基底弯曲

由于薄膜在沉积的初始阶段是薄膜材料在基底表面的形核过程，此时薄膜的应力是由形核的表面能与晶核及基底的界面能共同作用的结果。若沉积的薄膜原子与基底材料的界面能较小，此时由于薄膜原子表面能的作用，薄膜原子聚集在一起，整体在基底上扩散，此时并不会产生基底材料的弯曲变形；反之，若界面能较大，则会观测到基底材料的弯曲（见图4-11）。

对于固体表面来说，必须强调表面自由能及表面应力这两个重要概念的差别^[29，30]。表面自由能γ是指在常温、常体积及等化学势条件下产生一个新的单位表面所需要的可逆功，而表面应力f_ij则为张量，它是为了维持外表面平衡对单位表面施加的力，它与表面自由能有如下的关系

f_ij=γδ_ij+∂γ/∂ε_ij或f=γ+∂γ/∂ε（对于各向同性表面） （4-7）

式中，δ_ij为Kronecker函数，ε为表面应变。

沉积初期薄膜材料由于表面能的作用还会对晶粒内部晶格尺寸产生影响。当晶粒的尺寸较小时，晶粒内部晶格尺寸较小，随着晶粒的尺寸增加，内部的晶格尺寸也增加。在这个阶段晶粒内部压力满足Laplace方程，即

P=-2f/R=K（δV/V₀）≈3Kδa/a₀ （4-8）

式中，f和R分别为晶粒的表面张力及尺寸；a₀及δa分别为正常体积单晶晶格的尺寸及在压力P作用下晶粒内晶格尺寸与正常体积单晶晶格尺寸的差异；V₀及δV分别为相应的体积及体积变化；K为晶粒的体积模量。

由此也可以得到晶粒内晶格尺寸a随晶粒尺寸r的变化规律，即

a（r）=a₀[1-2f/（3Kr）] （4-9）

由于晶粒表面对基底作用是通过表面应力及晶粒与基底的界面应力来实现的，Spaepen^[19]指出对基底材料的弯曲变形来源于两个方面的因素，一是由于晶粒内部的压力导致的弯曲，这是主要因素，它导致的基底材料的曲率κ满足方程κ₁=-4fsin²θ/（t³_sE_s），其中，θ为晶粒与基底材料的浸润角，E_s及t_s分别为基底材料的杨氏模量及厚度。二是由表面应力f_s及界面应力f_i引起的，它满足方程κ₂=6（f_s-f_i-f_fcosθ）/（t²_sE_s）。综上所述，即使是在成膜的初始阶段，人们对应力的产生机理也并不完全一致，如Abermann的Laplace压力机理及Cam-marata等^[31]的闭锁应力机理。

随着薄膜沉积过程的进行，每个独立的晶粒会融合在一起，组成连续的薄膜，大量的研究表明^[18]，当薄膜完全连续时，薄膜内的压应力达到最大值。在晶粒合并的过程中，不仅会产生应力而且会使应力释放^[32]，合并过程中的拉应力产生可能有两种机理^[18]：一种是由于薄膜生长所引起的，也就是说由于薄膜晶界的原子密度小于晶粒内的原子密度，晶粒的生长主要是用来填充晶界^[32]；另一种机理是由已经沉积的薄膜材料原子的扩散所引起的，也就是说使得空位或者缺陷消失^[18]。很明显这两种机理均是由于薄膜生长的非平衡本质所引起的。

考虑晶粒合并过程中的应变能变化及晶界能的变化，Chaudhari^[32]给出了一个定量的模型来计算薄膜在晶粒合并过程中的内应力。对于典型的金属薄膜，在初始晶粒尺寸小于1.3nm时计算的临界应力为6×10¹¹dyn/cm²（1dyn/cm²=0.1Pa），应力计算公式为

(www.xing528.com)

式中，ΔL为单位面积晶界上理想晶体与含晶界的晶体的体积差；d₀及d分别为初始及终了状态时的晶粒平均尺寸，并且应用Au薄膜的实验数据得到的值为0.1nm。

当然，在实际情况中，由于应力的释放，不可能达到这么高的值。Doerner和Nix^[18]基于Chaudhari的理论进一步分析了晶粒生长过程中应力的动态变化，包括成膜过程中空位及缺陷的影响，并且得到了驱动晶界运动的压力差。Hoff-man^[33]也认为拉应力的产生是由于晶粒外表面受拉伸形成晶界引起的。此时，由于两个孤立的晶粒外表面形成晶界会产生能量的降低，正是这个能量差促使晶粒合并。Nix和Clemens^[34]将这种晶粒合并过程看作为裂纹的闭合过程，从而提出了一个模型来计算此时的内应力。应力的表达式为

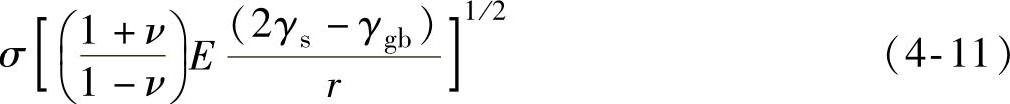
式中，E及ν分别为材料的杨氏模量及泊松比；γ_s及γ_gb分别为晶粒的表面自由能及晶界能；r为晶粒的半径。

应用该表达式计算的结果比实验测定的结果高很多^[34-36]，这是由于他们没有考虑晶粒在合并过程中的应力释放，包括晶粒在基底材料表面的滑移，不同晶粒形状在不同时间内的合并及晶体内部的缺陷运动等。应用有限元方法，Seel等^[36]重新计算了晶粒合并过程中的能量变化，并且得到了总能量的最小值与晶粒合并高度存在一定的关系。在他们的模型中，应力的释放采用如下的表达式

式中，C₀为仅与材料相关而与温度及应力无关的常数；σ为薄膜内的平均应力；t为薄膜的厚度；k为玻耳兹曼常数；T为温度；Q为考虑晶界及表面扩散的驱动能。

晶粒合并过程中的应力可以表示为

式中，q为常数，大小在1～10之间；其余参数的物理意义与（4-12）式相同。

Freund和Chason^[37]应用Hertz弹性接触理论研究的一维、二维及三维晶粒的合并过程，并且得到了与Seel等模型^[36]相似的结论，在他们的模型中，q=2^[35]。同样，Suh等^[38]基于不同的接触力学模型来研究晶粒的合并过程，并且详细讨论了应用各种接触模型的计算结果。由于在实际的薄膜生长过程中，晶粒在合并过程中的大小及形状不同，并且在时间上是随机的，应力的产生在同一时间包含不同的机理。针对这样的问题，Hearne等^[39]通过控制薄膜晶粒的生长形状从而详细研究晶粒合并过程中的拉应力。针对Stoney公式在测量薄膜内应力的局限性，Freund等^[40]提出了一个模型来测量薄膜的内应力，基于这个模型测量了半圆柱晶粒合并过程中的内应力，并且证明了Freund和Chason模型及Seel等的模型与实验结果吻合得很好。Zhang等^[41]分析了Stoney公式和基于Stoney公式基础上的各种修正方法及其他近似方法在描述单层薄膜残余应力时的误差，指出了各类方法的适用范围。考虑薄膜和基底的边缘效应，他们又提出了一个具有封闭解的模型来描述薄膜的法向应力及薄膜与基底的界面应力^[42]。

当薄膜成为连续的薄膜时，对于原子移动能力较高的材料，如铜和银，薄膜内的应力又转化为压应力，并且逐渐达到一个定值，如图4-10所示。这个定值在100MPa数量级，而材料的双轴模量在100GPa数量级，也就是说每1000个原子可以有一个原子发生畸变^[19]。Chason等^[43，44]构造了一个模型来模拟在该阶段的应力变化，他们认为在这个阶段产生的压应力主要是由于在薄膜沉积过程中的薄膜表面非平衡状态所引起的。在他们的模型中，应力的可逆变化是由于表面及晶界的能量差所引起的，随着沉积过程的进行，这个能量差导致沉积的原子不断地填充晶界；反之，当沉积停止时，晶界处的原子又移动至薄膜表面，从而实现在这个阶段薄膜内应力的可逆变化，其一维薄膜内应力的表达式为

式中，σ_i为晶粒合并过程中的拉应力值；σ₀为晶界处每进入一个原子所产生的压应力值；N_gb为进入或者离开晶界的原子数，它是一个与表面能和界面能差相关的函数，并且随着沉积过程的进行而不断变化，a为原子间距，h为薄膜厚度。

最终稳定的内应力值为

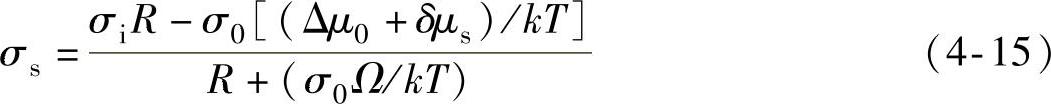
式中，Δμ₀为非生长条件下薄膜表面与晶界的能量差；δμ_s为由于沉积的粒子数产生的表面自由能的增加；k为玻耳兹曼常数；T为温度；R为描述生长速率的量；Ω为沉积原子的体积。

但是，Koch等^[45]最近通过铁薄膜的实验证明了这种产生压应力的机理在整个应力的产生过程中所占的比例很小，并且通过薄膜合并成连续薄膜之前的毛细现象得到证实。而Friesen与Thompson在随后的同一杂志上发表一篇关于Koch等文章的评论^[46]，他们认为Koch等的结论有几个缺点。首先，他们认为晶粒生长过程中可逆的内应力变化并不是由于生长过程中断导致的再结晶过程，因为再结晶过程及晶粒生长是不可逆的^[27]。其次，对于应力的可逆变化是由晶界迁移所产生的机理也是不可信的。最后，Koch等应用表面能而不是应用表面应力来计算岛合并之前的内应力也是有误的。

我国学者在这方面的研究也进行了大量的工作。基于凝聚体改进的TFD（Thomas，Fermi及Dirac）模型及弹性力学方法，程开甲先生等从一个全新的视角分析了薄膜内应力的产生机理，指出本征应力起源于薄膜材料与基底材料在界面处的电子密度差，给出了理论上计算连续薄膜内应力值的方法^[47]，并且证明了薄膜内应力产生的机制是微观表面电子密度连续，这也提供了一种降低薄膜材料内应力的方法，即降低薄膜与基底材料的表面电子密度差。刘继峰等^[48]在对CoSi₂薄膜的研究中证实了这一点，由于B的表面电子密度高于Si，他们在Si基底中掺杂不同浓度的B以改变基底与薄膜材料的电子密度差来制备多晶CoSi₂薄膜，实验结果表明，高掺杂B的p型Si基底上形成的CoSi₂薄膜中的内应力低于低掺杂B的Si基底上形成的CoSi₂薄膜。在实验测量薄膜的内应力方面，陈焘和罗崇泰^[49]详细介绍了国内外薄膜应力实验的研究进展，并且讨论了控制薄膜应力的几种方法。钱劲等^[50]通过微梁实验证明了薄膜内的应力并不是均匀的，而是沿厚度方向梯度分布的。邵淑英等^[51]则从几个方面介绍了薄膜应力，包括：产生机制、释放机制、控制技术及测量技术。

综上所述，薄膜生长过程是一个复杂的物理化学过程，不同材料的薄膜具有不同的生长方式，而不同的生长方式又会导致不同的内应力状态，需要不同的模型来描述。关于内应力的产生机理及其演化过程，人们并没有完全达成一致的观点，而薄膜内应力又是影响薄膜材料性能的重要因素。因此，在这个领域还有许多工作可以进行研究。