量化原理：将模拟信号转为二进制数值

量化（Quantization）是用二进制数组读出各取样时刻模拟信号的振幅值。由于取样时刻的模拟信号振幅值是随机变化的，但量化所用的二进制数的位数不可能是无限多的任意数值，例如3bit二进制数组最多只能读取8（2³）个等级的电平变化，16bit的二进制组最多可读取65536（2¹⁶）个电平变化等级，因此，必须通过四舍五入的方法将随机连续变化的模拟信号的振幅值变换为相应的二进制数值。

取样脉冲量化读出的电平与模拟信号振幅之间的差值称为量化误差（Quantization Error）。量化误差对信号而言是一种噪声，也称为量化噪声（Quantization Noise），如图3-4所示。量化位数越多，量化精度越高，信号失真越小，量化噪声也越小。

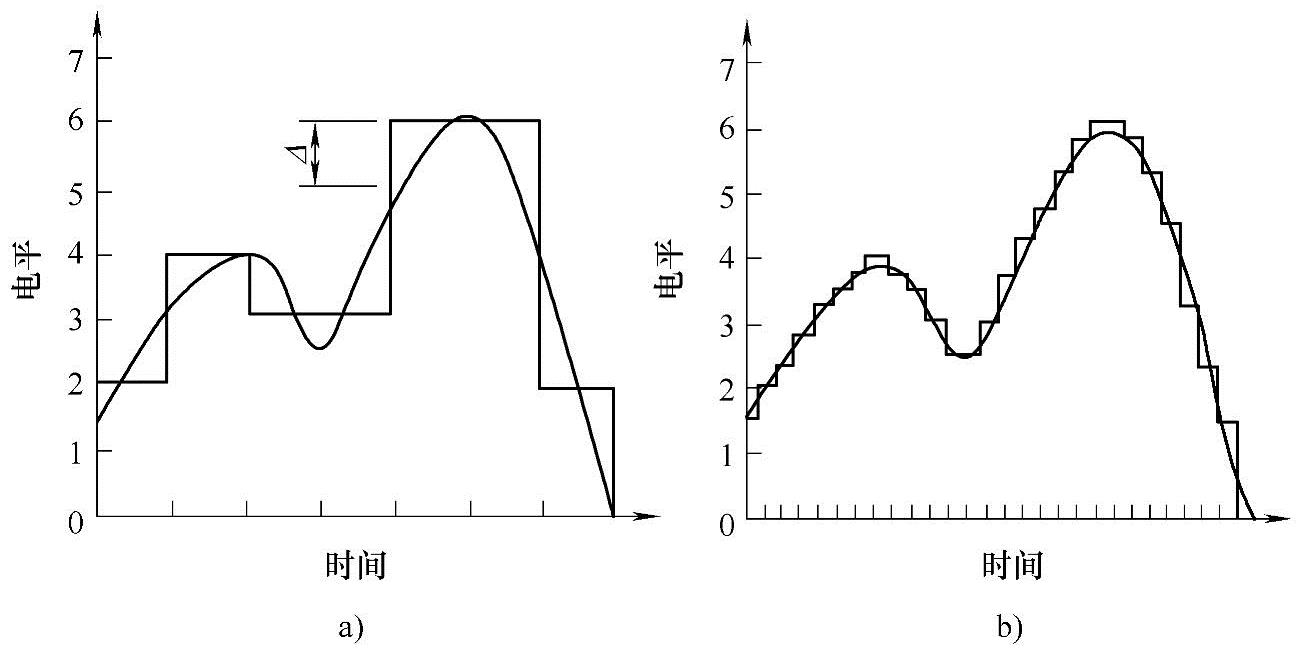
图3-4 量化误差与量化位数的关系

a）3bit的量化波形 b）6bit的量化波形

采用均匀量化（即等量化阶梯）的数字音视频信号，量化后的信噪比（dB）为

式中 n——量化位数（bit）；

m——信号性质的统计常数，正弦波信号的m为3.01。(www.xing528.com)

如果量化位数n=16bit，信号为正弦波，那么量化后的信噪比为

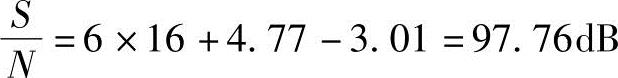
不过，同样是16bit量化，信号不是正弦波，而是变化速率较快的小振幅信号，常数m会更大，信噪比会降低。

当输入信号的振幅超过最大量化电平时，超过部分的输入信号，其量化输出不再增加（称数字削波），产生一种过载噪声（Overload Noise）。数字量化的过载表现为输出急剧饱和，因此在模拟-数字转换过程中为避免输入信号过载，在A-D转换器的输入端应采用限幅装置。

量化位数决定读取模拟信号强弱变化的范围，因而数字音视频的动态范围（dB）可表示为

数字音视频信号的动态范围=20log2ⁿ （3-3）

式中 n——量化位数（bit）；

例如：n=16时，信号的动态范围=20log2¹⁶=96dB。