调压调速原理解析

1.调压调速的性质

小李打开笔记本，开始说道：“以前曾经说过，当改变定子电压时，临界转差不变，临界转矩和电压的二次方成正比，电压越低，临界转矩越小，如图6-10a中之曲线①、曲线②和曲线③所示。

以恒转矩负载为例，电压下降后，转速略有下降，如图a中之A、B、C点所示。

由图可以看出，电压下降后，转差和转差率将增大。所以，改变电压的调速实质上属于改变转差率的调速。

但对于恒转矩负载来说，调速的范围很小，并无实用价值。如果像风机那样的二次方律负载，将工作点移至KS段，则在降压后的运行点分别是D、E、F点，降压后的转速分别是n_MD、n_ME和n_MF，由图6-10b可知，转速范围是较大的。

这里，我有几个问题没有想明白。

第一个问题，KS段不是非稳定区吗？为什么二次方律负载可以运行呢？”

张老师说：“这里，我们有必要补充一下关于稳定运行的讨论。”

2.KS段稳定运行的讨论

（1）恒转矩负载 在图6-11a中，曲线①是电动机在降压后的机械特性，曲线②是负载的机械特性，负载转矩是T_L。假设拖动系统在Q点运行，转速为n_Q，我们来看看它是否稳定？

如果由于某种原因，转速上升为n_X1，由曲线①知，电动机的电磁转矩将增大为T_MX1，大于负载转矩，拖动系统的转速非但不下降，反而更加上升，直至进入到AK_X段中的Q′点为止。可见，它在KS段是不能稳定运行的。

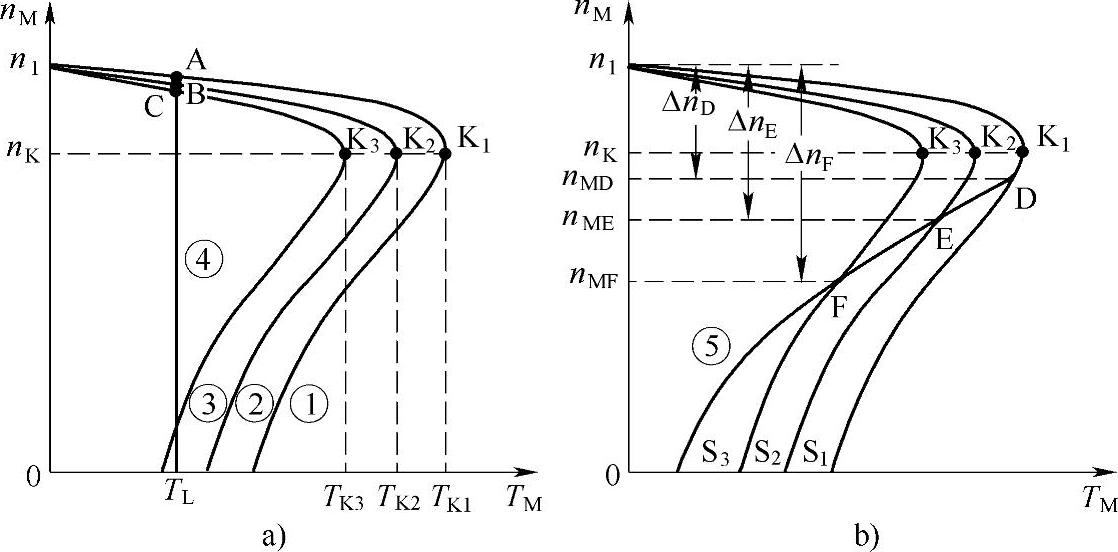
图6-10 调压调速原理

a）恒转矩负载时 b）二次方律负载时

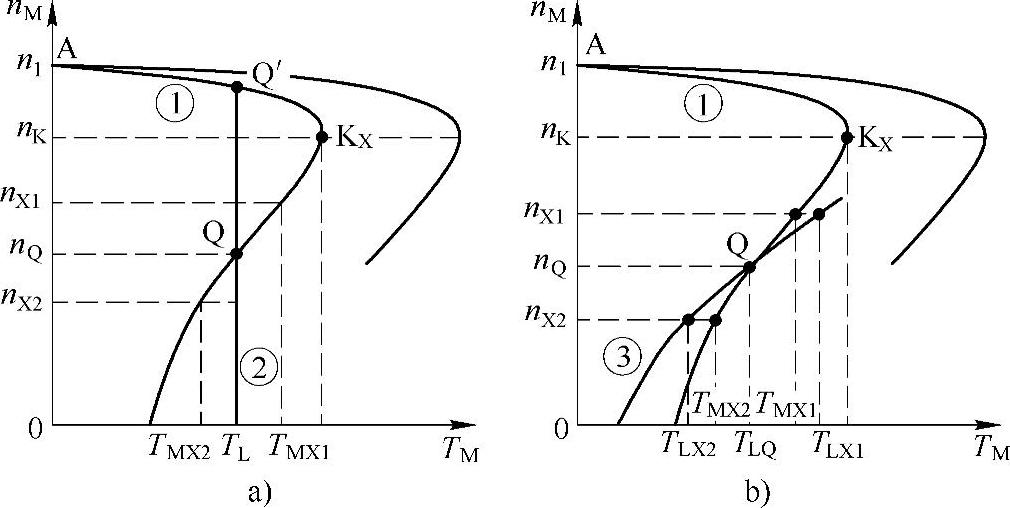
图6-11 KS段的稳定运行

a）恒转矩负载 b）二次方律负载

（2）二次方律负载 如图6-11b所示，曲线③是二次方律负载的机械特性。也假设拖动系统正在Q点运行，这时的负载转矩是T_LQ，转速是n_Q。

当由于某种原因，转速上升为n_X1。由曲线①知，电动机的电磁转矩增加为T_MX1，但由曲线③知，负载转矩增加为T_LX1，比电磁转矩增加得更多：

T_LX1＞T_MX1(https://www.xing528.com)

于是，拖动系统将减速，工作点回到Q点。

反之，如由于某种原因，转速下降为n_X2。由曲线①知，电动机的电磁转矩将减小为T_MX2，但由曲线③知，负载转矩减小为T_LX2，比电磁转矩减小得更多：

T_LX2＜TMX2

于是，拖动系统将增速，工作点又回到Q点。

所以，二次方律负载在KS段是能够稳定运行的。下面，你说一下调速的过程吧。”

3.调速过程

小李说：“如图6-12a所示，假设电动机的机械特性如曲线①所示，当负载转矩为T_L1时，拖动系统的转速是n_M1，工作点为Q₁点。

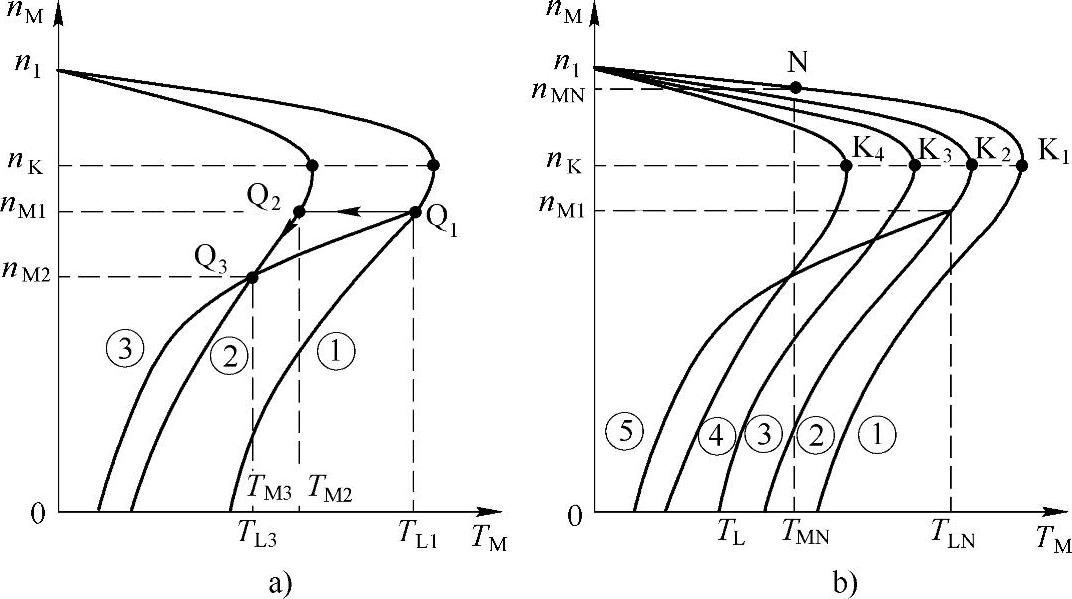
图6-12 调压调速的实际应用

a）调速过程 b）应用特点

今降低电压，电动机的机械特性如曲线②所示，在刚降压的瞬间，电动机的转速因为惯性而未变，系统的工作点跳转至Q₂点，电动机的电磁转矩减小为T_M2，小于T_L1，电动机于是减速。随着转速的下降，电动机的电磁转矩沿着曲线②下降，与此同时，从曲线③可知，负载转矩也随转速的下降而下降，而且降得更多，到Q₃点时，电动机的电磁转矩和负载的阻转矩重又平衡（相等）。这时，转速已经下降为n_M2了。

4.应用特点

这里又有一个问题，如图6-11b所示，拖动系统的转速岂不是不能到临界转速以上运行了？此外，负载转矩快要接近于临界转矩了，电动机岂不是没有了过载能力？”

“问得很好。”张老师高兴地说：如果要采用调压调速的方案，在为负载选择电动机时，就必须注意两点：

（1）电动机的额定转速应该比负载的额定转速大一挡。例如，如果负载的额定转速是960r/min，电动机的额定转速应该选择1460r/min的。

（2）二次方律负载主要指风机和水泵，而风机和水泵是不大可能过载的，所以电动机的额定转矩应该比负载的额定转矩小一些，如图6-12所示。

“转差那么大，会不会过电流呀？”小李又问。

“因为电压降低后，磁通会随之减小，所以只要选择适当，是不会过电流的，但这时电动机的效率较低，损耗较大，所以电动机的温升可能要高一些。”