如何计算起动过程中的功耗？

1.起动过程中的加速度

在谈到起动过程的具体计算时，小李写出了一个公式：

式中 T_J——拖动系统的动态转矩，N·m；

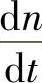——拖动系统的加速度。

接着，小李问：“这拖动系统的动态转矩取决于飞轮力矩和加速度的大小，怎么理解？”

张老师笑着说：“这个公式应该理解为：当拖动系统的飞轮力矩等于GD²时，拖动系统的动态转矩T_J和加速度之间的关系，如果把式（4-3）改写为

就比较容易理解了。式（4-4）表明，拖动系统的加速度和动态转矩T_J成正比，而和飞轮力矩GD²成反比。有了式（4-4），就可以求出起动时间了，你来试试吧。”

2.起动时间

这个问题难不倒小李，他立即在纸上写了起来，并且说：“由式（4-4）：

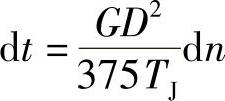
拖动系统的转速从n₁改变为n₂所需的时间：

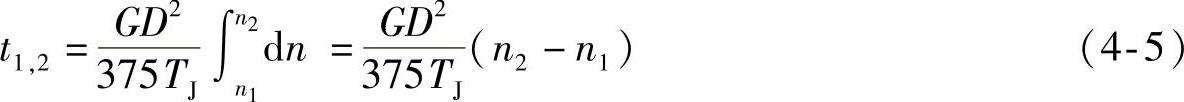
式中 t₁，2——转速从n₁改变为n₂所需的时间，s；

n₁——改变前的电动机转速，r/min；

n₂——改变后的电动机转速，r/min。(www.xing528.com)

起动时，电动机的转速从0上升到额定转速n_MN，所以

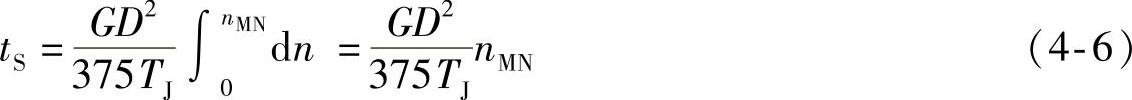
式中 t_S——起动时间，s。

式（4-6）表明，和起动时间有关的因素：

（1）飞轮力矩 飞轮力矩越大，起动时间越长。

（2）动态转矩 动态转矩越大，起动时间越短。

老师，起动时间短了，有什么坏处吗？”

3.起动太快存在的问题

张老师一边拿出一张图来，一边说：“起动太快了，针对不同的机械，会有不同的问题，举例说明如下：

（1）带式输送机 带式输送机在停止状态，传输带必然是松弛的，如图4-6a的上部所示。起动太快，传输带在短时间内迅速地绷直，传输带将因受到冲击而缩短寿命。

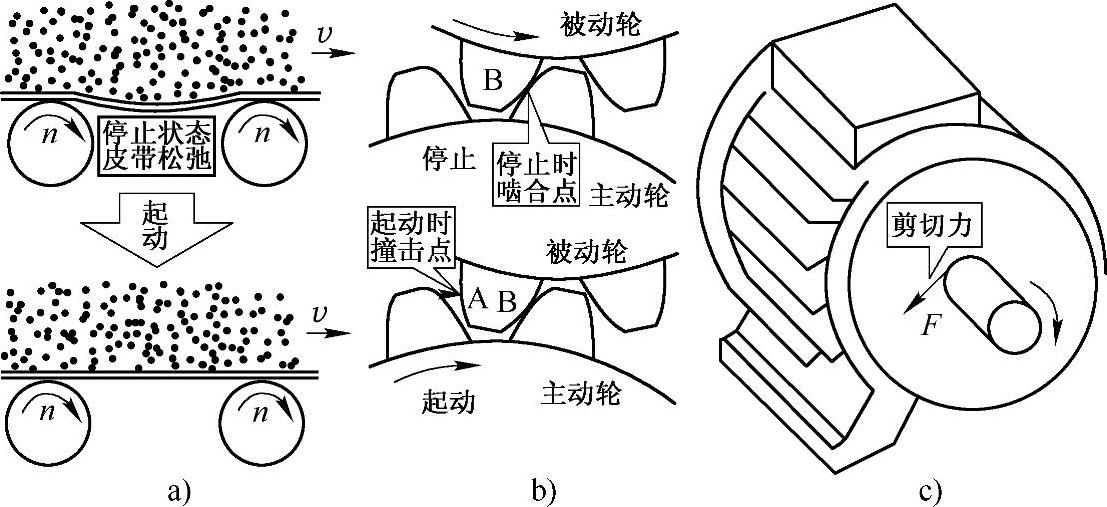
图4-6 起动太快存在的问题

a）带式输送机 b）齿轮 c）电动机的轴

（2）齿轮 如图4-6b所示，齿轮在上次停机时的啮合点在B点，当重新起动时，如起动太快，则被动轮的A点处将受到撞击，影响其寿命。

（3）电动机的轴 电动机的轴上常常带着很重的负载，起动太快，会使其输出轴受到很大的剪切力，也会影响其寿命。其实，不仅是电动机的轴，拖动系统中所有的轴也都会受到损伤。

（4）水泵的供水系统 水泵属于二次方律负载，其起动过程的动态转矩如图4-4b所示，T_J是很大的，又如图4-6a所示，其飞轮力矩又很小。所以，起动过程极为迅速。据美国AB公司的资料说，水泵的供水系统在全压直接起动时，起动时间只有0.25s。供水系统的流量在0.25s的时间里，从0迅速地上升到额定流量，将导致严重的水锤效应，具有很大的破坏力。”