探究电磁转矩的表达式的分析介绍

张老师在喝了一口茶后，又继续说：“关于电磁转矩，有两个基本表达方式：

1.物理表达式

就是上面说的式（3-14）：

式中 I_2a′=I₂′cosφ₂——转子等效电流的有功分量，A。

就是说，电磁转矩的大小和转子电流的有功分量成正比。

2.参数表达式

物理表达式主要用于对电磁转矩进行定性的分析，但它并未揭示电磁转矩和电动机各参数之间的关系，难以进行定量的分析。

根据式（3-7），电磁功率还可以表述为：

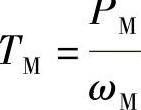
由此导出电磁转矩的参数表达式：

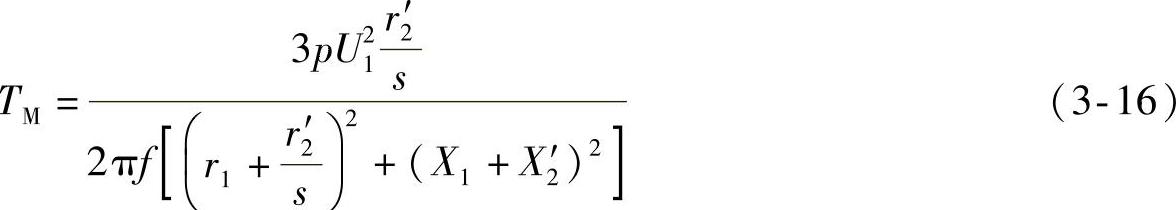
3.转矩-转差率曲线

式（3-16）表明，异步电动机的电磁转矩T_M是转差率s的函数，但因为在分子和分母上都有s，一时难以看出T_M和s之间究竟是怎样的关系，所以，有必要作出它们之间的关系曲线。今分析如下：

（1）s=1转速等于0，也就是电动机还没有旋转起来时的状态，称为起动点，如图3-8中之S点所示。把s=1代入式（3-16）就可以得到起动转矩：

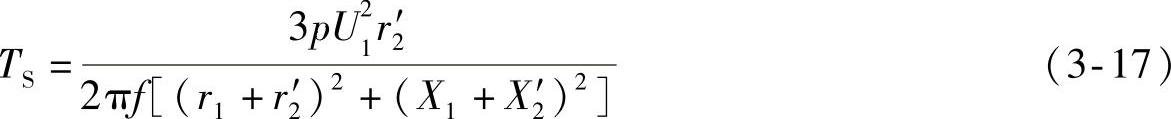
式中 T_S——起动转矩，N·m。

（2）s=1的邻近区间 在分母上，因为s≈1，并且：

r₁+r₂′＜＜X₁+X₂′

所以，如果把（r₁+r₂′）忽略不计，则在s=1的邻近区间，电磁转矩近似于：

式（3-18）表明，当s从s=1逐渐减小（转速上升）时，电磁转矩T_M是增大的，如图3-8中之箭头②所示。”小李抢着说：“我明白您的思路了，对于另外一头的分析，我来试试吧。

（3）s=0 s=0，就是电动机的转速等于同步转速：

n_M=n₁，Δn=0

这时，转子绕组不切割磁力线，其感应电动势E₂和电流I₂都等于0，电磁转矩T_M也等于0。所以，这一点的坐标是：

s=0，T_M=0

也就是坐标原点。

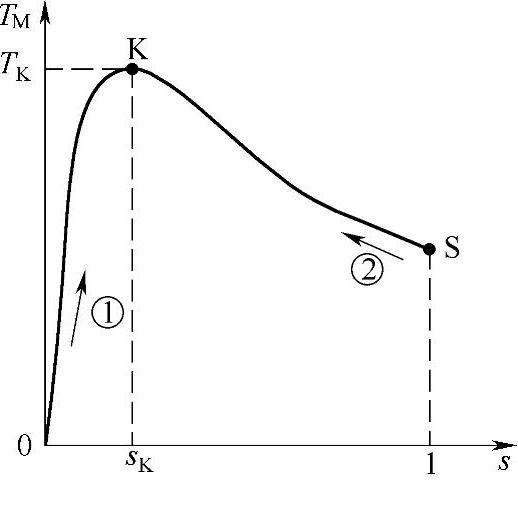
图3-8 T_M=f（s）曲线

（4）s=0的邻近区间 在s=0的邻近区间，（r₂′/s）将变得很大，在式（3-16）中：

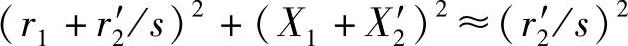(www.xing528.com)

于是，式（3-16）可近似地表达为

式（3-19）表明，在s=0的邻近区间，电磁转矩T_M是和转差率s成正比的，如图3-8中的箭头①所示。

（5）T_M=f（s）曲线的临界点 以上的分析表明，在s=0的邻近区间和在s=1的邻近区间，电磁转矩T_M的变化趋势是相反的。所以，T_M=f（s）曲线必有拐点，如图3-8中之K点所示。

对不对？”小李望着张老师，问。

张老师满意地说：“很好，这个拐点称为临界点。它说明，异步电动机的电磁转矩是有限度的。”

小李又说：“T_M=f（s）曲线OK段的物理意义很容易理解：当转差率增大（也就是转差增大）时，转子绕组切割磁力线的速度加快，感应电动势和电流增大，所以电磁转矩也增大。可是，在K点以后，转差率再增大，为什么电磁转矩反而减小了呢？”

张老师说：“看看式（3-15）所示的电磁转矩的物理表达式吧，电磁转矩并不是和转子电流I₂′成正比，而和转子电流的有功分量I₂′cosφ₂成正比。再看看第二章的式（2-18）：

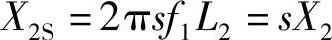
它说明，随着转差率的增大，转子绕组的漏磁电抗也增大，转子等效电路的功率因数减小。所以，转子电流的有功分量I′₂cosφ₂实际上是在减小的，电磁转矩当然也就减小了。”

小李问：“临界点的位置怎样确定？”

张老师说：“T_M=f（s）曲线有拐点的含义，用数学语言来说，就是它有一个极大值。所以：

令^d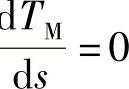，就可以得到临界转差率：

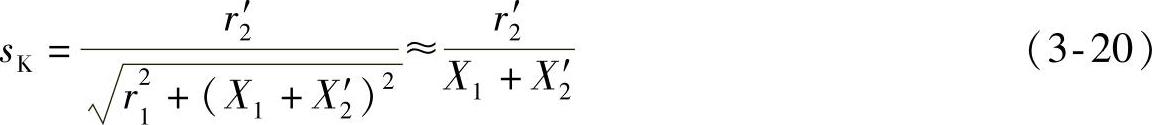
式中 s_K——临界转差率。

式（3-20）表明，临界转差率的大小和转子回路的电阻成正比。这个结论很重要，因为在绕线转子异步电动机里，转子回路里是可以串联电阻的，从而也就改变了发生临界转矩的位置。

将式（3-20）代入式（3-16），整理后，可得到临界转矩：

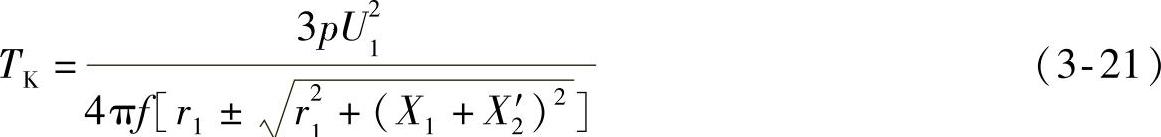
式中 T_K——临界转矩，N·m。

式（3-21）分母中的根号前，电动机状态时取‘+’号，发电机状态时取‘-’号。

又，因为：

r₁＜＜X₁+X₂′

所以，r₁可以忽略不计，则式（3-21）可近似为

由此式可以明显地看出，临界转矩的大小和电压的二次方成正比。这也是一个很重要的结论，因为临界转矩实际上就是电动机能够产生的最大转矩。所以，其大小说明了电动机的带负载能力。也就是说，异步电动机的带负载能力和电源电压有很密切的关系。”

小李又问：“老师，在电机学书里，只画出T_M=f（s）曲线。而在电力拖动书里，却还要把它改画成机械特性曲线，是什么原因？”

张老师说：“电机学书是讲述各种电机的特性，横向之间一般不作比较。但电力拖动则是研究各种电动机在拖动负载时的特点，在为负载选择电动机时，需要进行横向的比较。转差率是异步电动机特有的，在用T_M=f（s）曲线来描述转矩和转速之间的关系时，显得有点另类。所以，都统一用机械特性来描述电磁转矩和转速之间的关系。你回去后，就准备一下这方面的内容吧。”

小李的归纳

异步电动机的电磁转矩