定子感应电动势在转子开路时的表现

首先，我们把转子笼型绕组的端环断开，让转子绕组开路。”

“这是为什么？”小李感到迷惑不解。

张老师说：“因为转子有了电流，也会产生磁场，问题就复杂了。根据由简到繁的原则，首先把转子电流的因素排除掉。转子既然没有了电流，它也就不会旋转了，处于静止状态。这样，就可以在没有任何干扰的情况下来观察定子电路。

我们曾经说过，旋转磁场要被转子绕组切割。其实，与此同时，它也要被定子绕组自己切割，也要产生感应电动势。现在，就来分析一下这定子绕组感应电动势的特点。

1.定子电动势波形

首先，我们只讨论磁场的基波分量，就是说，认为：磁场在空间是按正弦规律分布的，如图2-6a所示。其磁感应强度是：

式中 B_X——任意位置的磁感应强度，T；

B_m——磁感应强度的振幅值，T；

x——任意位置和中性线的距离，m。

根据物理学知识，导体在切割磁场时的感应电动势是：

式中 e_1X——定子任意位置导体里的感应电动势，V；

l——导体的有效长度，m；

v——导体切割磁力线的线速度，m/min；

E_1m——定子绕组感应电动势的振幅值，V。

式（2-7）表明，定子绕组的感应电动势也是正弦波。

2.感应电动势频率

假设旋转磁场的转速为n₁，感应电动势的频率就由你来分析吧。”

小李对着图2-6，思考了一会儿，就开始说：“很明显：

（1）磁场每转一转，感应电动势就交变一次，相当于一个周期；

（2）每分钟旋转n₁转，则每秒钟旋转n₁/60转，感应电动势就交变n₁/60个周期。所以，感应电动势的频率是：(www.xing528.com)

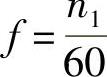
对不对？”

“这是一对磁极时的情形，要是有p对磁极呢？”张老师提醒说。

小李仿照着张老师的图2-6，画出了4极电动机旋转磁场和绕组里的感应电动势，如图2-7所示，然后说：“当有两对磁极时，磁场每旋转一转，电动势将交变两周，频率就增大了一倍。依此类推，当有p对磁极时，电动势的频率应该是：

式中 f——频率，Hz；

p——磁极的对数；

n₁——旋转磁场的转速（同步转速），r/min。

图2-7 定子绕组的感应电动势（2p=4）

a）磁场在初始位置 b）磁场旋转了π/2 c）磁场旋转了π d）磁场旋转了3π/2 e）电动势瞬时值

对照式（2-8）和式（1-13），可以看出，感应电动势的频率是和电源频率相同的。”

小李说完，望着张老师，意思是问：对不对？

张老师点了点头，又补充说：“事实上，如果把式（1-11）代入式（2-7），可以得到电动势瞬时值的表达式：

e₁=E_1msinωt （2-9）

式中 e₁——电动势的瞬时值，V；

ω——角频率，ω=2πf。

在这里，需要强调的结论是：感应电动势e₁和电源电压u₁是同频率的正弦量。

3.感应电动势性质

因为旋转磁场是由定子电流产生的，就是说，定子绕组切割的是自己的磁场，感应电动势e₁本质上是自感电动势e_L，所以，转子开路时的定子电路实际上就是一个电感电路。定子绕组里的电流，是电源电压u₁克服自感电动势e₁的结果。