相量图的旋转矢量和曲线图的介绍

1.旋转矢量

小李拿出了一张图，说：“相量图是从旋转矢量演变来的。以电压为例，当矢量U_m以角速度ω逆时针旋转时，它在Y轴上的投影正好是电压瞬时值的表达式，如图2-1a所示：

u=U_msinωt （2-1）

式中 u——电压的瞬时值，V；

U_m——电压的振幅值，V；

ω——角速度，rad/s；

t——时间，s。

由式（2-1）得到电压的瞬时值和旋转角度ωt之间的关系曲线如图2-1b所示。因为正弦量交变一周所需要的时间称为一个周期T，相当于旋转矢量旋转了2π。所以，角速度ω可以计算如下：

式中 T——正弦量的周期，s；

f——正弦量的频率，Hz。

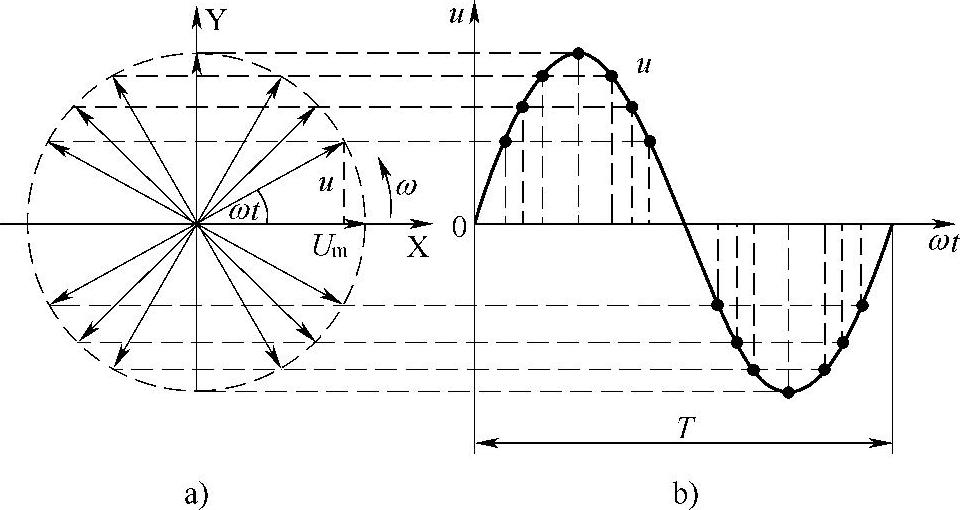
图2-1 旋转矢量(www.xing528.com)

a）U_m在旋转 b）Y轴上的投影和时间的关系

2.相量图

如果又有一个电流矢量I_m和电压矢量U_m之间的夹角是φ，两者同时以相同的速度逆时针方向旋转，如图2-2a所示。则电压矢量在Y轴上的投影如图2-2b中之曲线①所示，而电流矢量在Y轴上的投影如图2-2b中的曲线②所示。由图知，电压u和电流i并不同时到达零值和振幅值，因为电压矢量和电流矢量的旋转速度是相同的，两者之间永远相差φ角，φ角称为相位差角。既然电压矢量和电流矢量的相对位置是不变的，在表明两者之间的关系时，就没有必要再旋转了，于是得到相量图如图2-2c所示。对不对？”

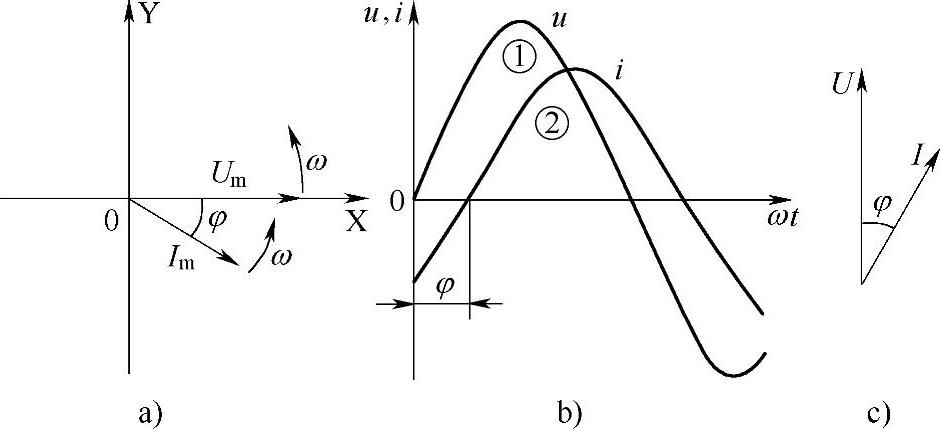
图2-2 相量图

a）两个旋转矢量 b）曲线图 c）相量图

小李一口气说完，心里颇为得意，觉得应该是不会有问题的。

张老师说：“说得很好。但在这里，必须强调两点：

第一点，只有正弦量才可以用旋转矢量来描述。

第二点，只有同频率正弦量之间，才可以用相量图来描述相互间的相位关系。

在电动机里，电动势和电流都是感应而得的，在进行讨论时，必须弄清楚：它们是不是正弦量？是不是同频率？”