脉动磁场与旋转磁场

1.脉动磁场的分解

根据三角学里‘积化和差’的公式，式（1-4）可以分解为

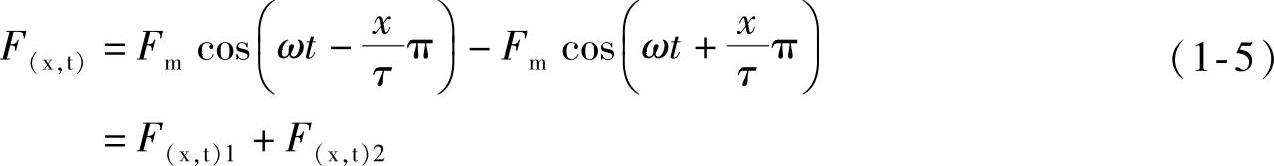
式（1-5）表明，脉动磁动势可以分解为两个部分：F_（x，t）1和F_（x，t）2。两者都是正弦（余弦）函数，它们的振幅值都只有脉动磁动势振幅值的一半：

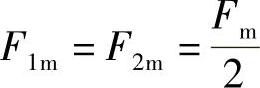
2.因子的分析

（1）在任何时刻t，总能够得到一个对应的x，使

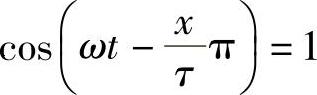
就是说，在任何时刻，都能得到磁动势的振幅值，这和脉动磁动势是不一样的。

（2）在不同的时刻，磁动势得到振幅值的位置也是不同的：

可见，磁动势的轴线是随时间而不断地移动的。或者形象地说，磁动势的轴线是在‘行走’的。所以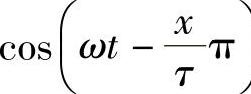，称为行波因子。不消说，因子也是行波因子，但

x=-2τft

所以，移动的方向和式（1-6）相反。”

小李简直听得出了神，他随手在纸上画了个示意图，兴奋地说：“啊，真有意思！这行波磁动势犹如人在行走，如图1-7a所示。因为电动机的定子是圆的，磁动势在定子内‘行走’的结果，就是在旋转，如图1-7b所示，对不对？”

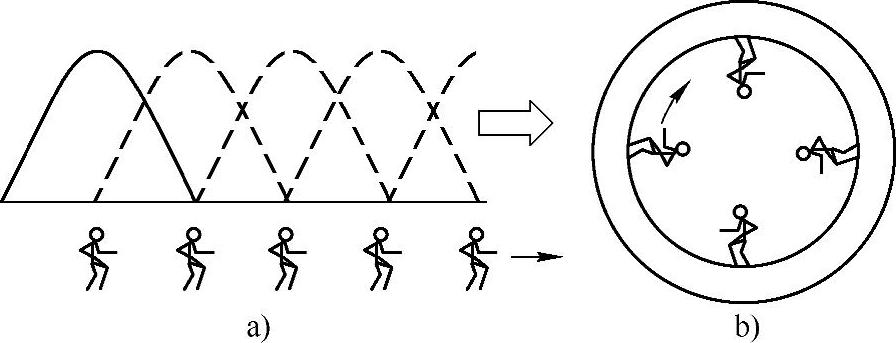
图1-7 行波示意图

a）行波的移动 b）行波在电动机里

张老师赞许说：“画得很形象。”

小李又说：“所以，式（1-5）就说明了，脉动磁动势可以分解成两个方向相反的旋转磁动势。但这是从数学公式里推导出来的，总觉得有点玄。”

张老师拿了一张纸，画了起来，说：“我们用图解的方法画出来，就一目了然了。如图1-8所示，F_（x，t）1是顺时针方向的旋转磁动势，F_（x，t）2是逆时针方向的旋转磁动势，当它们以相反的方向旋转时，合成磁动势是不是脉动的？”

“式（1-5）里F_（x，t）1和F_（x，t）2中间的‘-’号说明了什么？”小李又问。

“这说明，在起始位置（x=0）时，F_（x，t）1和F_（x，t）2是相等而相反的，如图1-8所示的那样。但就宏观效果而言，这里的‘-’号或‘+’号的实际效果是没有什么区别的。”张老师回答说。

“我在一本书上看到，旋转磁动势也可以分解成两个脉动磁动势，”小李一边说，一边在纸上画出了如图1-9a所示的示意图，说：“当磁动势在空间以速度ω旋转时，它在两个坐标轴上的投影就是两个互相垂直的脉动磁动势：

这也是从数学概念上分解出来的，有实际意义吗？”。

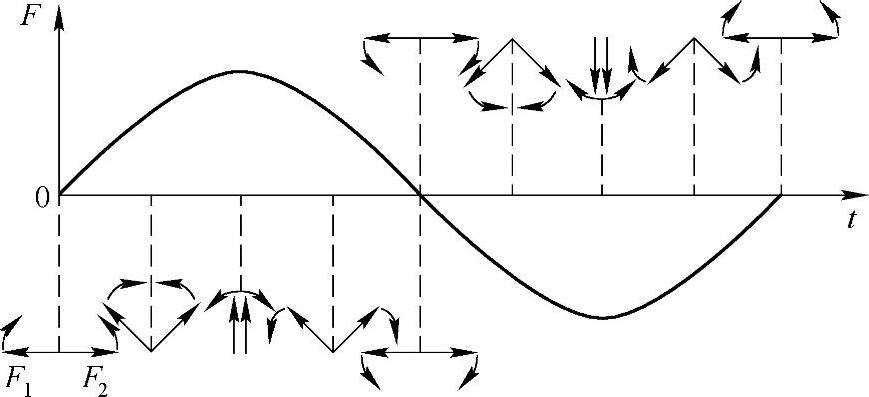
图1-8 脉动磁场分解成旋转磁场

3.旋转磁动势的分解

张老师就在小李的图旁边又画了个图1-9b，说：“有啊，例如在定子里安排两组互相垂直的绕组α和β，如图1-9b所示。在这两组绕组里，分别通入两相交变电流：

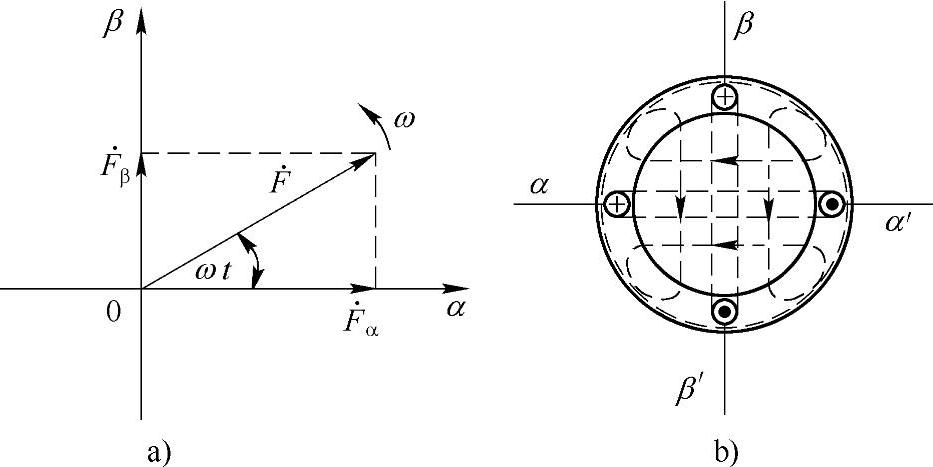
图1-9 旋转磁场的分解

a）分解旋转磁场 b）两相磁场

式中 i_α——α相电流的瞬时值，A；

i_β——β相电流的瞬时值，A；(www.xing528.com)

I_m——电流的振幅值，A。

毫无疑问，它们将分别产生各自的脉动磁动势F_α和F_β，你观察一下，它们的合成磁动势有什么特点？”

小李接过图，说：“我来试试看吧。首先假设：电流从相头流入时为‘+’，从相尾流入时为‘-’。由式（1-7）：

当t=0时：

i_α=0，α相的磁动势F_α=0；

i_β=-I_m，β相的磁动势为负的最大值。合成磁动势如图1-10b所示。

图1-10 两相旋转磁场

a）两相电流 b）t=0 c）t=3T/8 d）t=3T/4

当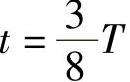时：

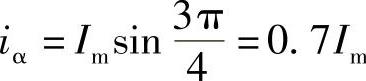，α相的磁动势F_α=0.7F_m；

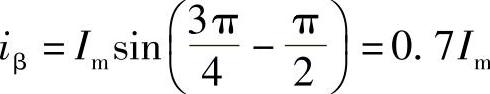，β相的磁动势F_β=0.7F_m。

合成磁场旋转了如图1-10c所示。

当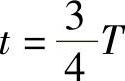时：

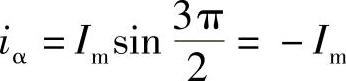，α相的磁动势F_α=-F_m；

，β相的磁动势F_β=0。

合成磁场又旋转了如图1-10d所示。

啊，这两个脉动磁动势合成的结果，的确是旋转磁动势。

这可真有意思：脉动磁动势可以分解为两个方向相反的旋转磁动势；而旋转磁动势又可以分解为两个互相垂直的脉动磁动势。

可是，在实际工作中，有没有两相电源呢？”

张老师又在纸上画了起来，同时说：“两相电源很少见，但两相电流是常见的。例如，在两个互相垂直的绕组里，让其中一个（β相绕组）和电容器串联，如图1-11a所示，今假设β相电流的振幅值只有α相的一半，如图1-11b所示：

I_βm=0.5I_αm

图1-11 两相电流的磁场

a）两相电路 b）两相磁动势 c）磁场轨迹

你看看，它们的合成磁动势是怎样的？”

小李一边在张老师的图上继续画了起来，一边说：“很明显，磁动势F_β比F_α超前。

当ωt=0时，F_α=0，F_β=0.5F_m，合成磁动势如F（x，t）1所示；

当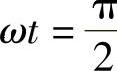时，F_α=F_m，Fβ=0，合成磁动势如F（x，t）2所示，比F（x，t）1逆时针旋转了90°；

当ωt=π时，F_α=0，F_β=-0.5F_m，合成磁动势如F（x，t）3所示，比F（x，t）2又逆时针旋转了90°；

当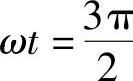时，F_α=-F_m，Fβ=0，合成磁动势如F（x，t）4所示，比F（x，t）3又逆时针旋转了90°。

可是，这合成磁动势的幅值却总在变化，也叫旋转磁动势吗？”

“当然也是旋转磁动势，”张老师边说，边顺手又画了个图1-11c。接着说：“不过，这旋转磁动势的轨迹是椭圆形的，称为椭圆旋转磁动势。

现在，我们该讨论三相电流的合成磁动势了。