单相磁动势的正弦分布特性

1.假设条件

假设绕组U₁U₂中通入电流后，磁动势在空间是按正弦规律分布的。”

“可是，事实上它不大可能是正弦分布的吧？”小李问。

张老师说：“这个假设可以从两个方面来理解：一是通过对定子绕组的适当安排，可以使定子磁动势的空间分布十分接近于正弦规律；二是作为一般分析，只需要考虑磁动势的基波分量就可以了，因此，可以把它理解为基波分量。

如果从U₁处切开后把线圈展开，则磁动势的空间分布如图1-5b所示。因为节距所跨的空间正好和半个圆周相对应，故相当于180°电角度（π）。

在线圈的中间位置，即距U₁半个节距处（如图中的x₁=τ/2处），对应的电角度是π/2，而在任意位置x₂处，其对应的电角度是：

式中 α——沿定子任意位置处对应的电角度；

x——沿定子任意位置和绕组起点之间相隔的距离（槽数）；

τ——绕组的节距（槽数）。

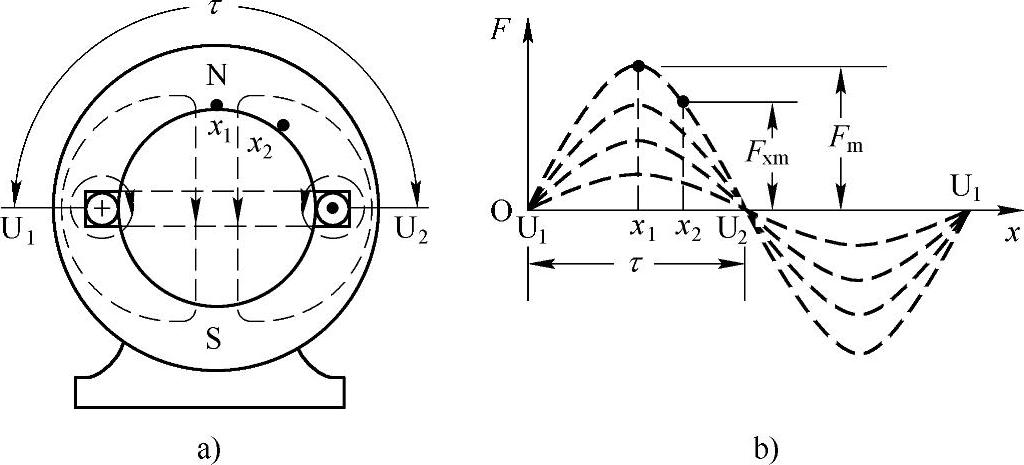
图1-5 单相磁动势

a）磁通的路径 b）磁动势的空间分布

显然，只有在x₁=τ/2处，才可能得到最大磁动势F_m。当在x₁处得到F_m时，在任意位置x₂处所能得到的磁动势的振幅值是：

式中 F（x）——任意位置时，磁动势的振幅值，A；

F_m——磁动势的最大振幅值，A。

2.交变磁动势

今向绕组U₁ U₂里通入按正弦规律变化的交变电流：

i=I_msinωt

式中 i——电流的瞬时值，A；

I_m——电流的振幅值，A；

ω——角频率，rad/s；

t——时间，s。

因为绕组的匝数是不变的，所以磁动势F的变化规律也是按正弦规律变化的：(www.xing528.com)

F（t）=iW=I_mWsinωt=F_msinωt（1-3）

式中 F（t）——磁动势的瞬时值，A；

F_m——磁动势的振幅值，A；

W——线圈的匝数。

所产生的磁动势大小，是随时间不断地变化着的。就是说，即使在x₁=τ/2处，也并不是总能得到最大磁动势的。因为，磁动势的大小要随时间按照正弦规律变化，或者说，是时大时小地脉动的，如图1-5b中的虚线所示。”

“老师，您为什么不用磁感应强度B或者磁通量Ф，而用磁动势F？”小李问。

张老师回答说：“因为磁感应强度B和磁通量Ф的大小要受到磁路饱和的影响，而磁动势只表示产生磁场的能力，和磁路的饱和程度无关。我们接着往下讨论吧。

3.任意瞬间任意位置的磁动势

（1）x₁=τ/2处的磁动势 如上述，在x₁=τ/2处，磁动势可以得到最大值F_m。这是因为电流是交变的，所以，在x₁=τ/2处的磁动势实际上是随时间按正弦规律变化的：

F（x）1=F_msinωt

（2）任意瞬间任意位置的磁动势 结合式（1-2）和式（1-3）得，任意瞬间任意位置的磁动势：

式中 F（x，t）——任意位置任意瞬间的磁动势，A。

4.驻波因子

式（1-4）中的称为驻波因子，其主要特点是：

（1）轴线位置不变 这是‘驻波’的最主要特征：尽管所有位置上的磁动势都是交变的，但磁动势轴线的位置始终不变，就好像‘驻扎’在那里一样。

（2）磁动势在原地交变 既然是‘波’，它一定是变化的，但它只是在原地变化。”

小李拿了一张纸，画了起来，说：“老师，对于驻波，能不能如图1-6那样地理解？就是说，在电动机定子的所有部位，磁动势都同时地按正弦规律交变着，但磁动势在不同位置处，交变的振幅值是各不相同的。

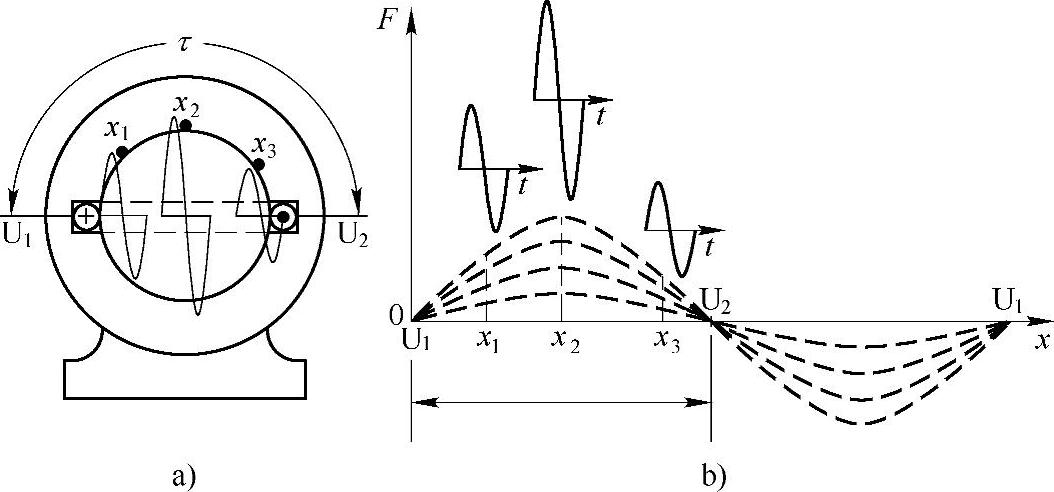
图1-6 驻波示意图

a）从电动机内部看 b）把定子展开后看

除此以外，我还依稀记得，在教科书上，把这样的单相磁动势称为脉动磁动势。并且，这脉动磁动势好像可以分解成两个方向相反的旋转磁动势，对不对？”

张老师很欣赏小李的这种能够根据自己的理解进行发挥的能力，笑着说：“很对。现在我们就来看看这脉动磁场和旋转磁场的关系。”