读图是运用正投影原理,根据视图想象出物体空间结构的过程。本节举例说明读组合体视图的基本方法,为以后看工程图样打下基础。
1)应将几个视图联系起来看
一个视图只反映两个方向的大小、尺寸和相对位置关系,一般情况下不能确定组合体的空间结构形状。除了圆锥、圆柱等一些回转体在图中借助符号φ、R、S能用一个视图确定其形状外,大多数情况下,一个视图可能与多个形体对应。
如图4.37所示的四组视图,所表达的形体各异,但它们的主视图完全相同。有时只看两个视图也不能完全确定物体的形状,如图4.37所示,(a)与(b)、(c)与(d)的左视图相同,但由于俯视图不同,表达的是不同的形体。由此可见,看图时必须将几个视图结合起来,互相对照,同时利用三等关系进行分析,这样才能准确地想象出物体的形状。
2)理解封闭线框和图线的空间含义
组合体视图中的图线主要有粗实线、虚线和细点画线。读图时,应根据投影原理和三视图投影关系,正确分析视图中的每条图线、每个线框所表示的投影含义。

图4.37 几个视图联系起来想象物体的形状
图4.38仅给出组合体的一个视图,它可能是多种不同形状物体的投影。随着空间物体形状的改变,在同样一个视图上,它的每个封闭线框以及每条线所表示的意义均不相同。分析图4.38所示的例子,可以看出以下性质:
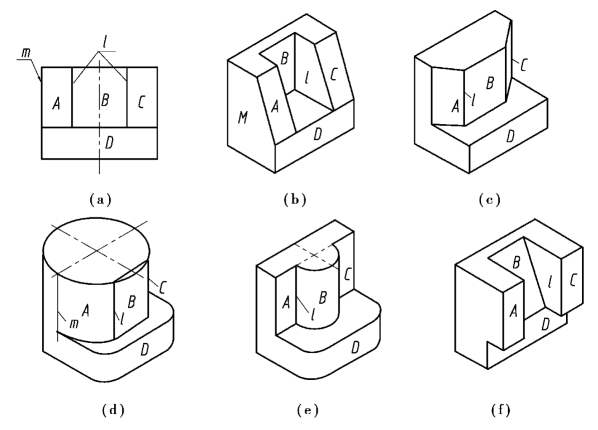
图4.38 视图中线和线框的含义
①视图上的每一条线(粗实线或虚线)可以是物体的下列各种要素之一的投影:
a.两表面的交线:如视图上的直线l,可以是物体上两平面交线的投影,如图4.38(c)所示,或平面与曲面交线的投影,如图(d)、(e)所示。
b.具有积聚性的平面或柱面的投影:如视图上的直线l和m,可以是物体上相应的侧平面L和M的投影,如图(b)所示。
c.曲面的转向轮廓线:如视图上的直线m,可以是物体上圆柱的某一转向轮廓线的投影,如图(d)所示。(https://www.xing528.com)
②视图中的细点画线可以表示:
a.回转体轴线的投影;
b.圆的对称中心线;
c.对称平面的投影。
③视图上的每一封闭线框(图线围成的封闭图形),可以是物体上不同位置平面或曲面的投影,也可以是通孔的投影。
a.平面:如视图上的封闭线框A可以是物体上投影面平行面的投影,如图(e)、(f)所示;或投影面垂直面的投影,如图(b)、(c)所示。
b.曲面:如视图上的封闭线框A可以是物体上圆柱面的投影,如图(d)所示。
c.曲面和其相切平面:如视图上的封闭线框D可以是物体上圆柱面以及和它相切平面的投影,如图(d)、(e)所示。
d.通孔的投影:如图4.36俯视图中底板和凸耳上的圆形线框表示圆柱通孔的投影。
④视图上任何相邻的封闭线框,必定是物体上两个不同表面的投影。如图4.38(c)、(d)、(e)中,线框C和B表示相交的两个面;图(b)、(f)中,线框C和B表示前后两个面。视图中大线框内含小线框,表示中间有凹、凸形体或空孔,如图4.39所示。

图4.39 从反映形体特征明显的视图看起
3)要先从反映形体特征的视图看起
读图时,必须从反映形体特征(形状特征和位置特征)的视图入手。主视图作为最重要的视图,通常能较多地反映物体的形体特征,因而读图时一般先从主视图入手,再联系其他视图来想象,便能较快地看懂物体。但有时组成组合体的各形体的形状和位置特征不一定全集中在主视图上,此时,必须善于找出反映形体特征的那个视图,再联系其相应投影,想象物体形状与位置便容易得多。
图4.39(a)给出了物体的三视图,主视图反映其形状特征较明显,但只看主视图,物体上的Ⅰ和Ⅱ两部分哪个凸出,哪个凹进无法确定,从俯视图上也无法确定是图(b)或(c)所示的形体,而左视图却反映了凸台及通孔的位置特征,将主、左两个视图联系起来看,能判定该组合体是图(c)所示的形状。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




