爆炸高速破片场速度场计算技术

对于含有金属壳体的装药结构，内部装药在爆炸时，会强烈冲击外部的金属壳体，使金属壳体破碎，产生大量的高速破片（几百米到几千米每秒不等），可以对周围的物体和人员产生严重的伤害，如手雷就是利用这个原理产生杀伤作用的。因此，快速计算装药壳体的破片的平均速度，对于快速估计爆炸场破片作用非常重要。

根据前人的研究成果，在一定的装药质量和装药壳体质量条件下，对于整体式圆柱形战斗部产生的自然破片，弹体的破碎与弹体结构、装药种类、弹体材料等因素有直接关系。目前，多采用半经验公式计算破片数量。爆炸产生的高速破片场的平均初始速度可以通过经典的格尼（Gurney）公式计算得到，具体的计算公式如下：

式中，是炸药的格尼常数，不同的炸药其数值不同，对于典型的5种炸药，其格尼常数如表11-6所示。C和M分别是炸药装药的质量（单位：kg）和金属壳体的质量（单位：kg），因此，公式中的C/M即为装填比。

表11-6　不同类型的炸药的格尼常数表

根据Mott破片分布公式得到破片的平均质量表达式：(www.xing528.com)

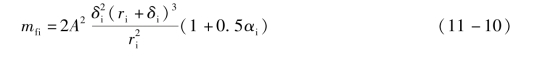
式中，ri，δi对应的是壳体的平均内径和壁厚，cm；A为与装药类型有关的常数，（g·cm-3）1/2，当选择的炸药为B炸药时，A=0.53，当选择的炸药为TNT时，A=0.42；α为炸药的装填比。从而破片的数量为：

采用TNT装药，不同装填比下破片的初速如表11-7所示。

表11-7　采用TNT装药，不同装填比下破片的初速