聚能装药射流形成理论优化分析

聚能装药爆炸时，可以观察到三个不同的时期，分别是射流形成阶段、射流断裂阶段、射流与靶板相互作用阶段。对于第一阶段，Birkhoff等人提出了定常流体理论，并被发展成为我们所熟知的PER（Pugh，Eichelberger and Rostoker）理论，这也是最常用的非定常模型。另外，Godunov等在1975年改进了定常理论来描述应变率的影响，其后来又进一步被Walters发展。

1.射流形成的定常Birkhoff理论

成形装药射流形成定常理论是由Birkhoff等建立的，它有如下假设：

（1）药型罩微元在罩轴线上被瞬时加速到最终压垮速度V0后不变。

（2）射流长度恒定且等于药型罩母线长。

（3）作用于罩壁各处的压力相等并且压垮角2β大于罩锥角2α。

（4）射流和杵体的速度和交叉处截面积都是恒定的。

图10-15所示为定常射流理论的药型罩压合过程分析，其中β表示压垮角，α是药型罩锥角的一半，V0为压合速度，V1为坐标移动速度（或A点的滞止速度），V2为射流微元流动速度，UD为爆轰波速。

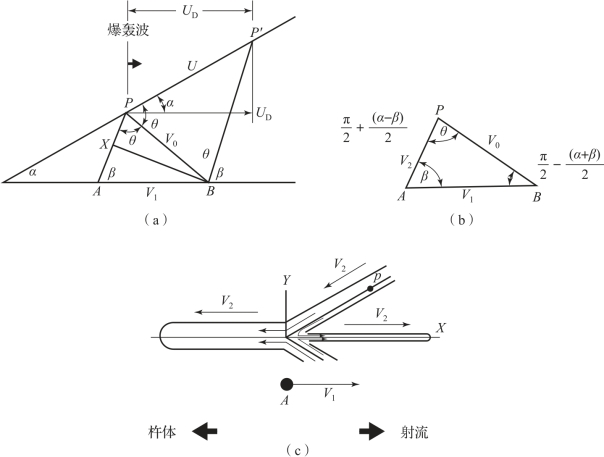
图10-15　定常射流理论的药型罩压合过程分析

（a）药型罩压合过程；（b）压垮、流动和滞止三者速度关系；（c）在动坐标A点上观察射流和杵体微元运动

认为该过程为定常理论的压合过程，根据三角关系，△PAB中的角可以表示为∠α和∠β的函数如下：

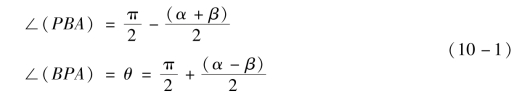
站在点A上的观察者将看到点P在以速度V2接近他，同时点A本身又以V1的速度向右移动，因此射流和杵体的速度可以由式（10-2）、式（10-3）计算：

又因为V1和V2分别是滞止速度和流动速度，由正弦定理有如下关系：

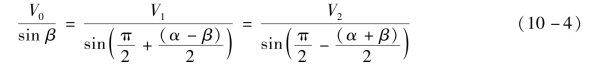
因此，V1和V2可以表示为

式中，压垮角β可以由式（10-7）求得

式中，U为爆轰波速沿方向的投影，可由U=UD/cos α求得，UD为爆轰波速。因此，射流和杵体速度可以如下计算：

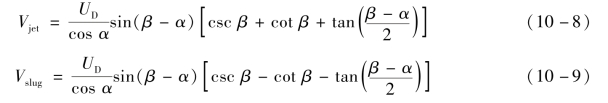
射流质量mj和杵体质量ms可由射流和杵体的质量和动量守恒关系求得，因此，可用式（10-10）、式（10-11）表示：

式中，m为药型罩初始质量。

此模型忽略了射流头部速度。计算出的射流长度大于圆锥的母线长度（药型罩的初始母线长度），这与最初的假设矛盾。并且，定常模型没有考虑速度梯度，而速度梯度是射流断裂的主要原因。

2.非定常PER理论

除了药型罩微元的压垮速度因各微元所处位置不同而不同外，非定常理论的基本原则与定常理论相同。压合速度在锥顶点取得最大值并向着锥底方向递减。假设压垮角向着锥底方向增大，那么，射流速度会在新的药型罩微元加入时降低。图10-16描述了恒定壁厚和不变锥角情况下的PER模型。另外，由于压合过程药型罩受压力很大，因而可以忽略罩材的内力。同时，已形成的射流中存在速度梯度，射流头部速度远大于射流尾部速度而导致射流拉长并断裂。

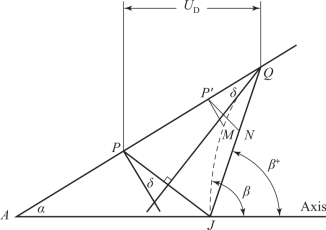
图10-16　压合速度为变量时的药型罩压合过程

由PER理论得到的非定常射流形成图解，如果压垮速度不变，则当P到达J点的同时P′到达N点，QNJ保持在一条直线上。但是，在PER模型中，P′的压合速度小于P，因而压合线是如图10-16所示的QMJ，所以非定常压垮角β比定常压垮角β＋要大。该假设是基于各微元足够小而不受相邻微元的影响的前提。药型罩微元并不是沿着原表面的法线方向移动，而是有一个小的Taylor偏向角δ，如图10-17所示。Richter提出了一个公式去求Taylor偏向角δ：

式中，ρl和TL分别为药型罩的密度和壁厚；K和ϕ0为取决于炸药种类和爆轰波作用于药型罩的入射角的常数；Te为驱动药型罩的炸药层厚度。

由非定常PER理论得到并表示出各个角度的几何关系，见图10-17。

式中，V0为相对于静止参考系的压合速度。

(www.xing528.com)

在压垮速度关系中，滞止速度和流动速度如图10-18所示，其中V1和V2可由V0通过正弦定理求得

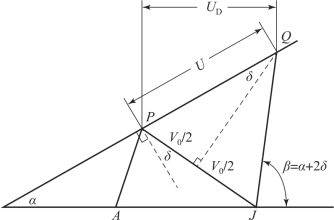
图10-17　非定常理论的参数几何关系

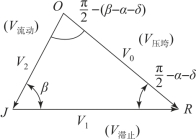
图10-18　压垮速度关系中流动速度和滞止速度

可得

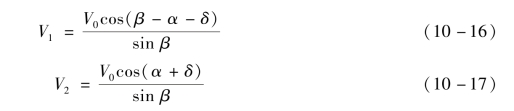
式中，V1为移动坐标的速度（滞止速度）；V2为微元在移动坐标中的流动速度；V0为在静止坐标系中的压垮速度。

Hirsh和Liu提出，非定常理论中的压垮角β可以如下计算：

式中，β＋为定常理论压垮角，β＋可如下给出：

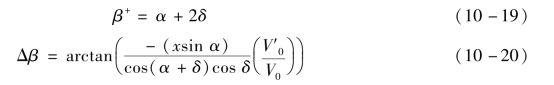
式中，x为沿着药型罩轴线从顶点到x点的距离。

因此，射流和杵体的速度可以如下计算：

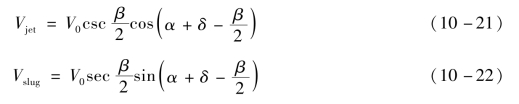
这些等式在定常理论（V0恒定）和非定常理论（V0变化）中都适用。

射流和杵体的质量满足

3.PER理论的改进

Allison和Vitalli的实验结果与PER理论有很好的吻合。但是Eichelberger发现了一些实验结果与PER模型预测结果矛盾，这是因为PER模型假设了微元压合到轴线上的加速过程是瞬时完成的（即加速度无穷大），如图10-19（a）所示。

Eichelberger提出药型罩压合的加速度是恒定的常数，即药型罩微元速度与时间呈线性关系，如图10-19（b）所示。该假设也被Carleone等人应用，其加速度值由式（10-25）给出：

式中，PCJ为所有炸药的C-J压力；TL和ρl分别为药型罩的厚度和密度；c为经验常数。Randers-Pehrson提出了更加精确的药型罩压合速度与时间关系，如图10-19（c）所示，其计算公式为

式中，τ为时间常数，可以由式（10-27）计算：

式中，M为单位面积上的原始质量；c1和c2为经验常数。

理论上，顶点部分有最大的压垮速度，因为它有最大的炸药-罩材质量比。但是，实际上并不是这样，因为邻近顶点的罩材没有足够的时间达到理论压垮速度，而在顶点之后的某个微元有最大速度。这种速度增大造成了称为反向速度梯度的现象，如图10-20所示。

很多作者尝试去解释当爆轰波到达金属罩时射流速度与爆轰波形状的关系。Behrmann、Birnbaum和Carleone改进了PER射流形成模型去考虑爆轰波对射流形成的影响。

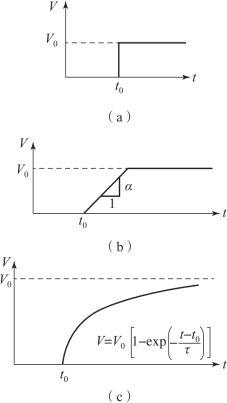
图10-19　药型罩微元速度与时间关系

（a）加速度无穷大；（b）线性关系；（c）指数关系

图10-20　反向速度梯度

沿着药型罩表面方向的爆轰波速U可以用UD/cos ζ（x）表示，其中UD是轴向爆轰波速，ζ（x）是爆轰波前沿法线与药型罩表面的夹角。因此，Taylor偏向角可一般表示为