气泡脉动及其影响因素探讨

与水下爆炸产生的主要爆炸波的运动几乎一样重要的是包含爆炸性气体产物或水蒸气的气泡的运动。如果发生核爆炸，则该气泡将包含大部分放射性碎片，因此追踪其进展非常重要。此外，气泡脉动会置换大量水，并经常产生振幅非常大的表面波。

水下气泡运动的最简单理论忽略了重力效应和可压缩性，并且基于控制具有球对称性的非稳态不可压缩流动的方程式的解。在此假设下，气泡脉动的径向速度与半径的平方成反比，并且从气泡表面（r=a）到较远距离的动量方程积分关系为

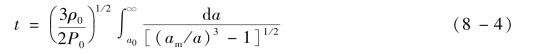
如果忽略气体的内部能量，则P0是流体静压力，而a0是初始气泡半径。气泡半径随时间的变化如图8-2所示。

如果气泡中心的垂直速度U向上，则由气泡产生的扰动可以用速度势来表示

使用方程式（8-5），我们可以建立以下形式的能量方程式：

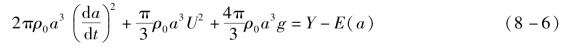
式中，z是气泡中心的高度；Y是爆炸释放的能量；E是气泡的内部能量。由于，式（8-6）有两个未知数，a和z。通过将气态球上的浮力的推力与周围水所获得的垂直动量相等，可以得到与a和z有关的第二个方程。

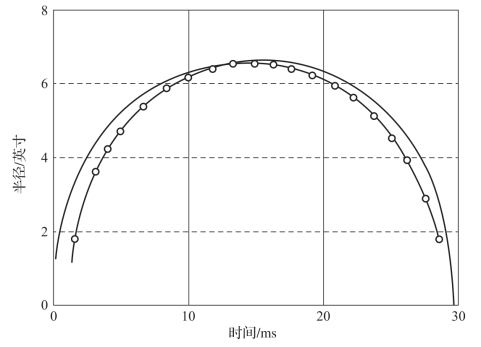
图8-2　泡沫增长的早期阶段

由式（8-6）和式（8-7）得出的气泡的组合振动和迁移如图8-3所示。这两个简单的理论都基于以下假设：气泡是球形的，并且受干扰的水具有向上和向下的叠加运动。在小型实验室测试和全面爆炸中对气泡运动的观察表明，实际的气泡行为要复杂得多。在第一个气泡收缩阶段，浮力作用占主导地位，并且使气泡的球形明显变形。气泡的下侧在最后的收缩期进入凹入状态，因此气泡整体上呈肾形。当气泡向上移动时，气泡边界上的流动在后凹部附近分离。形成一个对称的循环芯，从而形成一个涡流环。然后，合并的气泡和涡流环一起向水的表面迁移。

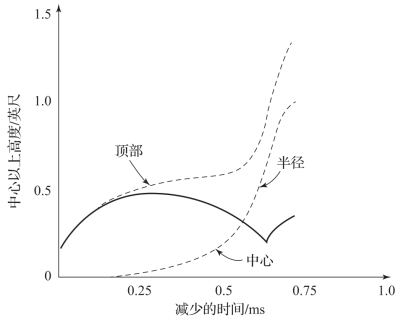
图8-3　球形爆炸气泡的脉动和迁移

最初提出的关于涡流环附着在气泡上的推测得到了直接和间接实验证据的支持。研究人员测量了由化学装药引起的水下深部爆炸产生的干扰，尽管气泡到达表面需要很长的行程时间，但产生的表面扰动的程度表明气泡以巨大的能量到达了那里。实际上，能量远大于基于简单球泡理论计算得到的值。但是，如果将涡流环与气泡结合，则在爆炸早期获得的大量动能会存储在由涡流环传递的旋转分量中，而在涡旋的振荡和迁移过程中，旋转几乎不会消耗掉这些泡沫的动能。

通过比较单个脉动气泡的能量与结合涡流环的气泡的能量，可以检验涡环理论的可行性。在组合运动中，气泡被视为希尔氏球形涡旋。

气泡外的水的运动不依赖于内部气泡运动的细节，而仅受气泡边界运动的影响。当前的气泡迁移理论基于气泡外部水的能量平衡以及整个气泡的动量方程，给出了气泡振荡的平移速度和周期的表达式。可以合理地得出结论，现有的迁移理论不受气泡内部涡旋运动模型的影响。因此，在进行计算时，可以使用平移速度和气泡周期的现有值。

气泡能由内部能、动能和势能组成。内部能量与气泡表面压力成正比。该压力取决于气泡半径和平移速度，因此与内部气泡运动无关。势能也与气泡内部的行为无关，因为它还取决于气泡半径和平均密度。因此，仅通过比较动能就可以揭示出其两个内部运动模型在气泡能量上的任何差异。

现在，在式（8-6）和式（8-7）中，唯一可能取决于内部气泡运动的项是E（a），这与气泡表面的压力成正比。因此，压力的值仅取决于气泡的半径及其向上的速度，而绝不受气泡内部运动的细节的影响。

从这些性质可以得出结论，气泡的迁移特性与气泡内部的运动方式无关。气泡是作为径向脉动球还是作为振荡的球形涡流运动，都不会影响气泡的向上移动速度和边界的周期性运动。两种运动方式的唯一区别在于气泡内部流体的能量。

气泡的动能是根据其作为振荡球形涡旋运动的假设计算的。假设半径a是时间的函数，当球形涡旋振荡时，相同的表达式立即适用。半径为a的球形涡旋以速度U移动时径向和横向速度分量的表达式为(www.xing528.com)

式中，r是从其中心测量的半径，θ是从垂直向上测量的角度。

球形涡旋的动能为

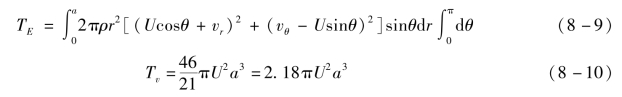
为了进行比较，在假设气泡仅沿径向脉动而完全不存在涡环运动的情况下计算其动能。

假定在任何给定时间，整个气泡的密度是均匀的，但它是时间的函数，则连续性方程为

式中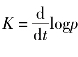，；vr是径向速度。式（8-11）的积分是

因为当r=0时，vr=0，令V为气泡边界的速度，则。然后式（8-12）在边界处成立，因此

脉动气泡的动能为

减少到

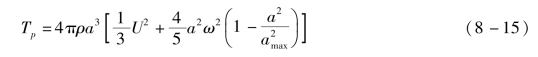
式中，a为在时间t时的气泡半径；amax为最大半径。令为气泡脉动频率，则V=amaxcos2ωt。

从式（8-10）和式（8-15）中，我们得出气泡作为球形涡旋运动时的动能与简单脉动气泡的动能之比，即

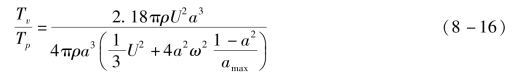
如果a=amax，则有

因此，球形涡旋的动能超过脉动气泡的动能达64%。在气泡波动的最大值和最小值之间，该增加将稍小。该结果与观察结果在定性上吻合。