炸药热能起爆机理简介

炸药在储存、运输、加工处理及使用过程中常会遇到不同的热源，如雷管中电热丝加热、炸药的烘干，装药前炸药的预热和熔化等。炸药在热源作用下能否发生爆炸？怎样发生爆炸？具备什么条件才能发生爆炸？热作用下发生爆炸同哪些因素有关？这些都与热爆炸（thermal explosion）机理有关。

热爆炸：凡是在单纯的热作用下，炸药在几何尺寸与温度相适应的时候能发生自动的不可控的爆炸现象均称热爆炸。热爆炸理论主要是研究炸药产生热爆炸的可能性、临界条件（温度、几何尺寸）和一旦满足临界条件发生热爆炸的时间等问题。热爆炸的临界条件就是指在单纯的热作用下，能够引起炸药自动发生爆炸的那些最低条件。

炸药在热作用下发生爆炸的理论探索是从爆炸气体混合物热爆炸问题的研究开始的。H.H.谢苗诺夫建立了混合气体的热自动点火的热爆炸理论。这一理论的基本观点是，在一定条件（温度、压力及其他条件）下，若反应放出的热量大于热传导所散失的热量，就能使混合气体发生热积累，从而使反应自动加速，最后导致爆炸。

弗兰克-卡曼涅斯基发展了定常热爆炸理论，这一理论进一步考虑了温度在反应混合气体中的空间分布。莱第尔、罗伯逊将热爆炸理论应用于凝聚炸药的起爆研究中，提出了热点学说。这一学说揭示了撞击、摩擦、发射惯性力等机械作用下炸药激发爆炸的机理和物理本质。布登、约夫等把热爆炸理论进一步扩展到起爆药的起爆研究中，并对热爆炸的临界条件的某些参数进行了计算。

就研究内容而言，热爆炸理论可分为定常热爆炸理论和非定常热爆炸理论。这里定常与非定常都是就温度与时间的关系而言，即炸药温度是否随时间变化。定常热爆炸理论研究的重点是发生热爆炸的条件，而非定常热爆炸理论则是重点研究具备热爆炸条件后，过程发展的速度。

1.均温分布的定常热爆炸理论

谢苗诺夫在如下三点假设下，建立了均温分布定常热爆炸的热平衡方程式，进而确定了热爆炸的临界条件：

（1）炸药各处温度相同，就是说炸药的里层和外层不存在温度差。这一假定适于研究薄层炸药的热爆炸，如铝盘中炸药的烘干过程，可以认为盘中炸药各处温度是均匀的。

（2）环境温度T0=常数，烘药时烘箱加热温度即为T0。

（3）炸药达到爆炸时的炸药温度T大于T0，但两者差值（T-T0）不大。

基于上述假定，可以建立炸药的热平衡方程式。

首先，炸药在温度T时单位时间内，由于发生化学反应而放出的热量Q1取决于化学反应速度W（g/s）及单位质量炸药反应后所放出的热量q（J/g），即

按照化学反应动力学，一级反应（炸药的热分解过程假定属于此种类型）在开始反应时的速度为

式中，Z为频率因子，它与分子的碰撞概率有关；E为炸药的活化能；m为炸药量；R为气体常数。

将式（3-2）代入式（3-1）得

与炸药发生化学反应的同时，单位时间内因热传导而散失环境的热量Q2为

式中，K为传导系数，J/（℃·s）；T为炸药温度；T0为环境温度。

可想而知，只有当单位时间内炸药反应放出的热量Q1大于散失给环境的热量Q2时，炸药中才有可能产生热的积累，而只有炸药中发生了热积累，才可能使炸药温度T不断升高，引起炸药反应速度加快，进而最后导致炸药爆炸。故炸药爆炸的临界条件之一必须满足

然而，达到热平衡只是爆炸的一个条件，要达到爆炸必须满足另一个条件，即放热量随温度的变化率超过散热量随温度的变化率，只有这样才能引起炸药的自动加速反应。所以爆炸的第二个条件为

由式（3-6）和式（3-8）可得热爆炸的临界条件为

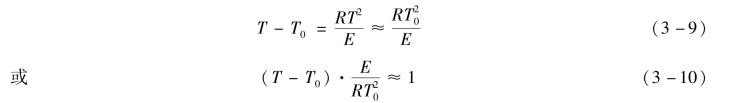
令，这里θ称为无因次温度。

显然，当无因次温度θ＞1时，炸药就可能发生热爆炸；当θ＜1时，炸药不可能发生热爆炸。式（3-10）还可用来估计在环境温度T0时，炸药达到爆炸必须具备的温度T。

2.不均温分布的定常热爆炸理论

假设容器中炸药各处温度不均匀，热平衡方程可写成

式中，为拉普拉斯算子；-λ∇2T为散失给环境的热量（λ为导热系数）；qZe-E/RT为炸药化学反应所放出的热。

式（3-11）用无因次温度θ变化可得

如果导热过程只与一维空间有关，并把x（距容器中心的距离）转化为无因子量（r为容器的半径），则

(www.xing528.com)

式中，l为常数，对于无限大平板状容器l=0，对于圆柱形容器l=1，而对于球形容器l=2。

在两面均匀加热时，式（3-14）的边界条件为

（1）在容器中心处，。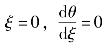

（2）在壁面处，ξ=0，θ=0。

卡曼涅斯基曾对l=0，1，2三种情况解出了式（3-14），所得热爆炸临界条件如表3-1所示。表中δK和θK为δ和θ的临界值。如果系统的δ＞δK，θ＞θK，则炸药就会发生爆炸。

表3-1　热爆炸临界条件

在Q-T坐标系内，Q1=Zmqe-E/RT为一条指数曲线，如图3-2所示，称这条曲线为谢苗诺夫得热线，而散热量Q2=K（T-T0）在Q-T坐标系中为一斜线，其斜率为K=tanα，图3-3所示为谢苗诺夫失热线。

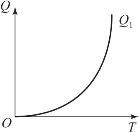
图3-2　谢苗诺夫得热线

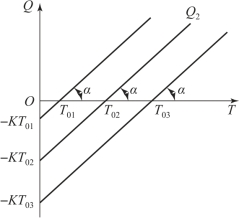
图3-3　谢苗诺夫失热线

失热线上的每一点的横坐标代表炸药的温度T，纵坐标代表相应的散热量。失热线和T轴的交点表示炸药的温度和环境温度T0相等，失热量Q2为零。失热线与Q轴的交点表示炸药温度T=0 K时环境传给炸药的热量（如图3-3中-KT01，-KT02，-KT03等所示）。显然，T轴以下失热线上各点所确定的炸药温度T都低于环境温度T0，此时环境对炸药加热。

从得热与失热关系容易看出，炸药热爆炸特性与炸药的活化能、炸药的分解反应热、炸药的热传导系数和热容、有效的加热面积及炸药的质量等因素有关。

将得热线与失热线画在同一个Q-T坐标系内（图3-4），而后分三种可能情况进行讨论分析。

图3-4　得热线与失热线可能出现的三种形式

（1）环境温度为T01时，由图3-4（a）可看到，直线和曲线有交点A，在A点左边，Q1＞Q2，得热大于失热，使炸药温度升高，升高到A点时Q1=Q2，在A点右边，Q2＞Q1，失热大于得热，使炸药温度降低，又回到A点。

所以，当介质温度较低时，炸药温度维持在TA，反应稳定地、缓慢地进行，不会自动加快，A点叫稳定平衡点。

（2）环境温度为T03时，由图3-4（b）可看到，曲线在直线的上方，在这种情况下，因环境温度T03很高，炸药在任何温度下，得热总是大于失热，炸药温度不断升高，最终导致爆炸。

（3）环境温度为T02时，由图3-4（c）可看到，曲线与直线相切，在切点C上，有Q1=Q2，而在C点以下和C点以上都是Q1＞Q2。在C点的左边，有Q1＞Q2，此时得热大于失热，温度升高，很快达到C点。在C点处，只需热量稍微增加一点，就会到达C点的右边，于是Q1＞Q2，得热大于失热，炸药温度迅速升高，最后导致爆炸，所以称C点为不稳定平衡点。

环境温度T02是量变到质变的数量界限，环境温度低于T02时，得热线与失热线相交，炸药将处于交点的温度，进行稳定的、缓慢的反应，不会导致爆炸。而当环境温度大于T02时，曲线将在直线上，得热大于失热，反应将自行加快，最后导致爆炸。T02是炸药能够导致爆炸的最低环境温度，称T02为炸药的爆发点。

所以，爆发点就是炸药在热作用下，其反应能自行加速而导致爆炸的最低环境温度。

应当指出，炸药的爆发点并不是爆发瞬间炸药的温度。爆发瞬间炸药的温度为TC［图3-4（c）］，爆发点是炸药分解开始自行加速时环境的温度，即为T02。从开始自行加速到爆炸要有一定的时间，称为爆发延滞期。在实验测定时，延滞期取5 min或5 s为标准，以便比较。

3.爆发点的影响因素

爆发点不是炸药的物理常数，因为它不仅与炸药性质有关，而且与介质的传热条件有关。如将测爆发点的铜壳改成铁壳或玻璃壳，炸药的爆发点就会明显地改变。对于同一炸药在相同的介质温度T0下，介质传热系数不同，若K1＞K2＞K3（或α1＞α2＞α3），如图3-5所示，在介质传热系数较小（K3）时，T0高于炸药的爆发点；相反，在介质传热系数较大（K1）时，T0低于炸药的爆发点。因为K=K1时，曲线Q1与Q2（T01）相交，T0低于爆发点；K=K2时，曲线Q1与Q2（T02）相切，T0是爆发点；K=K3时，曲线Q1＞Q2（T03），T0高于爆发点。

由此可见，散热条件不同，爆发点也会变化。所以，如果炸药仓库通风条件不好，炸药可能在较低温度下发生爆炸。

炸药药量对爆发点也有一定的影响，如图3-6所示。当药量增大时，单位时间内反应放出的热量增大，所以药量大的曲线1在药量小的曲线2的上面。因此，药量大，爆发点就低。

图3-5　传热系数对爆发点的影响

图3-6　药量对爆发点的影响

由此可见，爆发点是易受各种物理因素影响的一个量。为了比较不同炸药的热感度，在测定爆发点时，必须固定一个标准实验条件。例如，采用同一种仪器、同一管壳，插到合金浴中同一深度（2.5 cm），用同一药量（0.05 g）等。

从上面讨论可以看出，很多炸药在热作用下发生爆炸是单纯的热机理，符合简单反应动力学热爆炸规律，但不少炸药如叠氮化钡、雷汞、TNT和硝化甘油等在热作用下发生爆炸的机理是自催化热爆炸。所谓自催化热爆炸是指足够量的炸药，其反应速度随着某一产物浓度的增大而增大，在反应速度增长到最大值前，系统中放热速度大于散热速度，这是反应的自动加速，由自催化作用和热作用共同决定，导致自动加速作用更激烈从而爆炸。

有些炸药在受热作用下具有链锁反应的特征，尤其是某些气体混合物，进行链锁反应，链分支大于链中段，即使温度不再升高，也会自动加速，出现等温链锁爆炸。如果炸药受热后不仅进行链锁反应，而且反应放热，随着温度的升高，链锁分支中断，活化中心的数目在短时间内增加得很快，反应会自动加速，从而出现链锁热爆炸。

热爆炸理论虽然是从气体爆炸理论引出来的，但这些基本点也适用于凝聚炸药热爆炸的情况。