渐开线齿轮啮合分析与优化

（一）齿轮传动比和平稳性要求

齿轮传动的传动比是主动齿轮转速与从动齿轮转速（或角速度）之比，用i表示，即

式中 n1，n2—— 主、从动轮的转速（r/min）；

ω1，ω2—— 主、从动轮的角转速（rad/s）。

齿轮传动的最基本要求：一是传动要平稳；二是承载能力要强。齿轮承载能力可通过改变齿轮尺寸参数、材质，以及加工工艺来提高，而齿轮传动平稳则要求瞬时传动比恒定不变，即传动比为常数。这是因为当主动齿轮以等角速度回转时，如果从动齿轮的角速度为变量，将产生惯性力。这种惯性力会引起机器的振动和噪声，影响工作精度，还会影响齿轮的寿命。为此，一般齿轮传动都要求瞬时传动比为常数。

（二）齿廓啮合基本定律

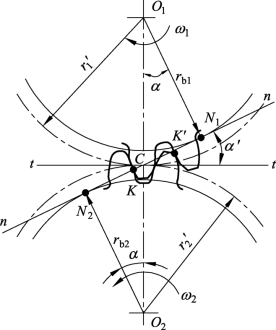
图7-3-4　渐开线齿轮啮合

(www.xing528.com)

凡能满足齿廓啮合基本定律的一对齿廓，称为共轭齿廓。理论上可作为共轭齿廓的曲线有无穷多，但在生产实际中除满足齿廓啮合基本定律外，还要考虑到齿廓曲线制造、安装和强度等要求。常用的齿廓有渐开线、圆弧和摆线等，其中渐开线齿廓在通用设备上应用最广。本书只介绍渐开线齿廓。

（三）节点与节圆

两齿轮啮合传动可视为两轮的节圆在做纯滚动。两个齿轮啮合时才会产生节点、节圆，单个齿轮没有这些概念。

（四）渐开线齿轮齿廓的形成

如图7-3-5所示，当直线NK沿一圆周做纯滚动时，直线上任意点K的轨迹AK，称为该圆的渐开线；这个圆称为渐开线的基圆，其半径用rb表示。A点是渐开线的起点，K点是渐开线上任意一点。由K点向基圆作切线为NK，N点是切点，直线NK称为渐开线的发生线。齿轮圆心O到渐开线上任意一点K的距离，称为渐开线K点的向径，用rK表示；rK与ON线段所夹锐角称为渐开线任意一点K的压力角，它也是渐开线任意一点K的速度vK方向和该点受力Fn方向所夹的锐角，用αK表示。rK与OA线段的夹角称为渐开线任意一点K的展角，用θK表示。

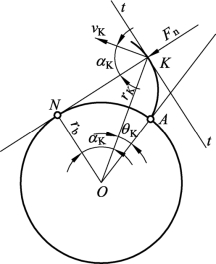
图7-3-5　渐开线的形成

任意两条反向的渐开线形成了渐开线齿廓。