直梁平面弯曲及内力分析

（一）直梁平面弯曲的概念

作用于杆件上的外力垂直于杆件的轴线，使杆的轴线由直线变为曲线，这种变形称为弯曲变形。如图3-2-30所示，铁路机车车辆轮轴受力变形。以弯曲变形为主的直杆称为直梁，简称梁。在受力简图中，通常以梁的轴线表示梁。

由梁的轴线和横截面的对称轴构成的平面称为纵向对称面，如图3-2-31所示。梁的外载荷都作用在纵向对称面时，则梁的轴线在纵向对称面弯曲成一条平面曲线，这种变形称为平面弯曲。平面弯曲是最常见、最基本的弯曲变形。本书主要讨论直梁的平面弯曲变形。

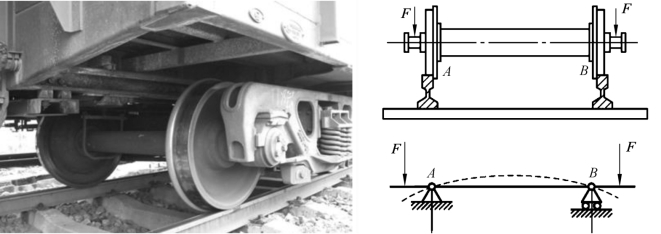
图3-2-30　铁路机车车辆轮轴受力

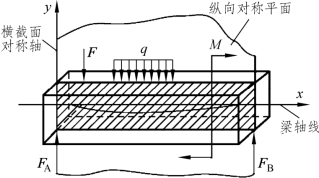
图3-2-31　直梁的纵向对称平面

（二）剪力和弯矩

1. 剪力与弯矩的概念

剪力是指作用线位于所切截面的内力；弯矩是指矢量位于所切截面的内力偶矩。与截面相切的内力QF称为截面上的剪力，它是与截面相切的分布内力系的合力；内力偶矩M称为截面上的弯矩，它是与截面垂直的分布内力系的合力偶矩。

2. 剪力与弯矩的正负号规定

梁某截面剪力与弯矩的正负号由该截面附近的变形情况确定。

（1）剪力的正负号规定。如图3-2-32所示，当截面发生变形时，使梁绕研究对象顺时针转动的为正剪力，逆时针转动的为负剪力。

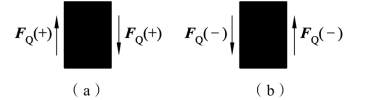
图3-2-32　剪力的正负号规定

（2）弯矩的正负号规定。如图3-2-33所示，当截面发生变形时，使梁变成凹形的为正弯矩，使梁变成凸形的为负弯矩。

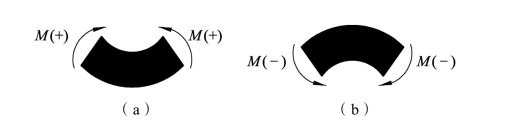
图3-2-33　弯矩的正负号规定

3. 剪力与弯矩的计算方法

根据截面法以及剪力与弯矩的符号规定，可建立复杂载荷作用下梁在任意截面的剪力和弯矩计算公式，举例说明如下。

例3-2-8 如图3-2-34（a）所示，简支梁AB=4 m，已知P1=20 kN，P2=40 kN，AF、BF为两端的支座反力，线段a=0.8 m，b=1.0 m，l=1.2 m，求距A端l处I—I截面的剪力和弯矩。

解 用截面法把梁分成两段，并标出剪力和弯矩，如图3-2-34（b）、（c）所示。

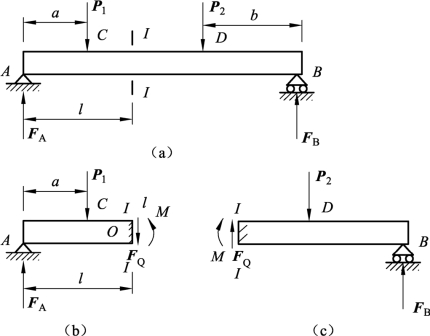
图3-2-34　截面法计算简支梁弯曲内力

（1）求支座反力AF和BF。

（2）求剪力QP。

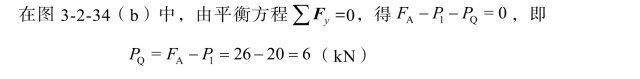
PQ的方向如图所示。

（3）求弯矩M。

（三）剪力图和弯矩图

一般情况下，梁横截面上的剪力、弯矩随截面位置的变化而变化。若以梁的轴线为x轴，坐标x表示横截面的位置，则剪力和弯矩可表示为x的函数，即

这种内力随截面位置变化的函数关系式，分别称为梁的剪力方程和弯矩方程。梁的内力随截面位置变化的图线，称为梁的内力图，包括剪力图和弯矩图。由内力图可以确定梁的最大剪力和最大弯矩及其所在截面（危险截面）的位置，以便进行梁的强度计算。

在工程上，用列方程的方法来绘制剪力图和弯矩图是一种最基本的作图方法，其作图步骤如下：

（1）求支座反力。根据静力平衡方程，求出梁的支座反力。

（2）列剪力方程和弯矩方程。根据梁的受载情况，分段列出剪力方程和弯矩方程。

（3）画剪力图和弯矩图。根据剪力方程或弯矩方程的函数关系式，分别判断剪力图和弯矩图的大致形状，然后描点连线，分别画出剪力图和弯矩图。

下面通过实例来说明剪力图和弯矩图的画法。

例3-2-9 一悬臂梁AB（图3-2-35），右端B受集中载荷F作用，左端A为固定端约束，约束反力为FA，约束反力偶矩为MA，已知F、l。试作该梁的剪力图和弯矩图，并求最大剪力和最大弯矩。

解 （1）列剪力方程和弯矩方程。以A端为坐标原点，在距A点x处任取一横截面，如图3-2-35（a）所示。由简便法可求得该截面上的剪力和弯矩分别为

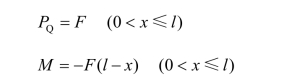
（2）画剪力图和弯矩图。根据上述剪力方程和弯矩方程，及截面剪力与弯矩的正负号规定，画出剪力图和弯矩图，如图3-2-35（b）、（c）所示。

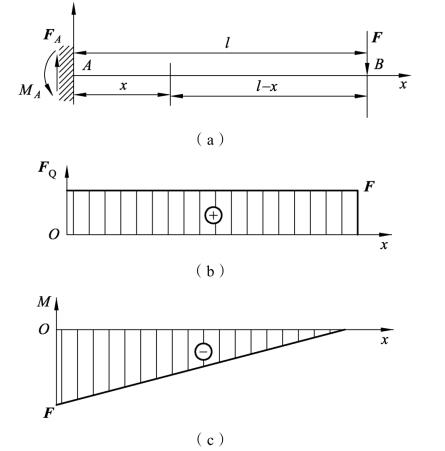
图3-2-35　悬臂梁

（四）弯曲时的强度条件和应用

一般情况下，梁的横截面上不仅有正应力σ，还有切应力τ。当梁比较细长时，弯曲正应力是进行梁强度计算的主要因素。

1. 弯曲正应力强度条件

求出梁横截面上的剪力和弯矩后，为了解决梁的强度问题，必须进一步研究横截面上各点的应力分布情况。若梁横截面上只有弯矩而无剪力，则所产生的弯曲称为纯弯曲。

梁弯曲时的强度条件为梁内危险截面上的最大弯曲正应力不超过材料的许用弯曲应力，即

式中 Mmax—— 梁的最大弯矩（N·m）；

WZ—— 梁的抗弯截面模量（m3）；

[σ]—— 材料的许用应力（Pa）。

矩形截面的抗弯截面模量计算公式为

式中 b—— 矩形截面的宽（m）；

h—— 矩形截面的高（m）。

圆形截面的抗弯截面模量计算公式为

式中 d—— 圆形截面直径（m）。

2. 弯曲切应力强度条件

一般情况下，梁满足了正应力强度条件，就可以满足切应力强度条件。但在某些情况下，如一些跨长较短，载荷靠近支座的梁以及腹板较薄的组合截面梁，它们的切应力就可能相当大，这时就有必要进行切应力的强度校核，即

一般最大切应力发生在最大剪力所在截面的中性轴处，其值根据截面的形状选择相应的公式来计算。

3. 强度条件的应用

在进行梁的设计时，先依据正应力强度条件计算，必要时再进行切应力强度校核。根据强度条件可以解决下述3类问题：

（1）强度校核：验算梁的强度是否满足强度条件，判断梁的工作是否安全。(www.xing528.com)

（2）设计截面：根据梁的最大载荷和材料的许用弯曲应力，确定梁截面的形状和尺寸，或选用合适的标准型钢。

（3）确定许用载荷：根据梁截面的形状、尺寸及材料的许用弯曲应力，确定梁可承受的最大弯矩，再由弯矩和载荷的关系确定梁的许用载荷。

例3-2-10 某铁道机车车辆轮轴受力如图3-2-36（a）所示。已知d1=160 mm，d2=130 mm，L=1.58 m，a=0.267 m，b=0.16 m，P=62.5 kN，[σ]=100 MPa，试校核该轴的强度。

解 画出轴的受力简图，如图3-2-36（b）所示。

（1）求支座反力。由于受力情况对称，两支座反力必然相等，即

（2）作弯矩图。列方程求解得

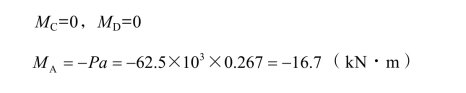
弯矩在CA、BD段均为斜直线，而在AB段为一水平线，作弯矩图如图3-2-36（c）所示。

（3）强度校核。AB段有最大弯矩，则

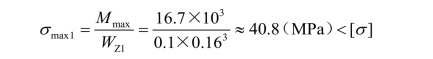
另外，在车轴外伸端与车轮接触处，因车轴直径较小（d2=130 mm），也可能是危险截面，必须校核。此处弯矩为M=Pb=62.5×103×0.16=10（kN·m），则

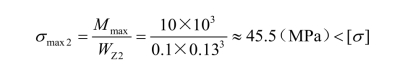
故此车轴是安全的。

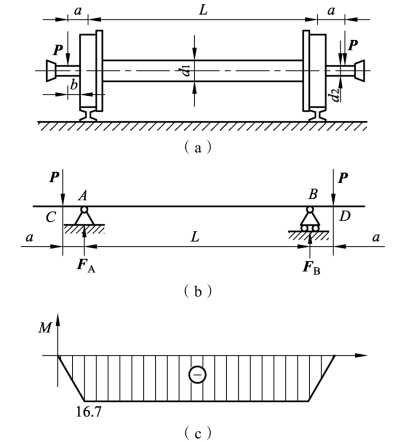
图3-2-36　某铁道机车车辆轮轴受力图

（五）提高梁强度的主要措施

1. 降低最大弯矩Mmax数值

（1）合理安排梁的支承。如图3-2-37所示，在所受载荷相同的情况下，图3-2-37（b）产生的弯矩是图3-2-37（a）弯矩最大值的1/5。因此集中力靠近简支梁的中点，可以提高梁的承载能力。

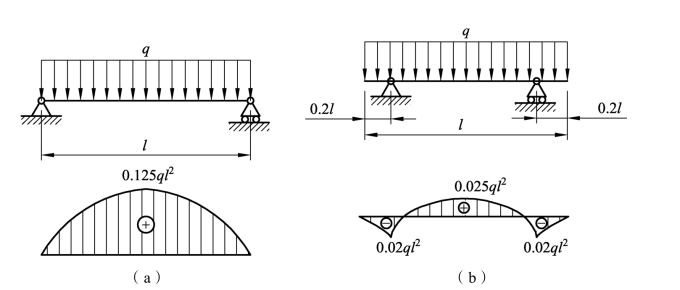
图3-2-37　合理安排梁的支承

（2）合理安排载荷。如图3-2-38所示，当简支梁AB在中点受集中力F作用时，其弯矩如图3-2-38（a）所示。弯矩的最大值出现在中点，且Mmax=Fl/4。当变成受两个集中力F/2作用后，如图3-2-38（b）所示，所受的载荷相同，但产生的弯矩最大值减小了一半。因此合理地安排载荷也可以提高梁的承载能力。

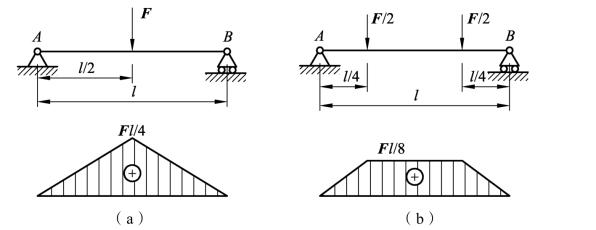
图3-2-38　合理安排载荷

2. 合理选择梁的截面

合理的截面即用较小的截面面积（即用材料少）得到较大的抗弯截面模量ZW。例如，工字形截面比矩形截面合理，而矩形截面又比圆形截面合理，所以铁路轨道常采用工字形钢轨。

3. 采用变截面梁

为了节省材料，减轻结构的重量，可在弯矩较小处采用较小的截面，这种截面尺寸沿梁轴线变化的梁称为变截面梁。

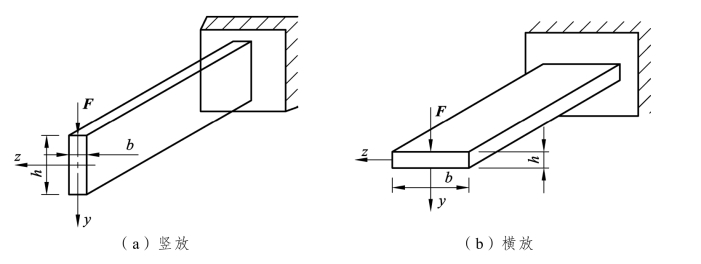
图3-2-39　梁的放置方式

若变截面梁每个截面上的最大正应力都等于材料的许用应力，则这种梁称为等强度梁，如图3-2-40所示的阶梯轴。

图3-2-40　阶梯轴

【思考】

提高梁强度的主要措施有哪些？这些科学合理的措施对你处理生活实践中的问题会有什么启示？

【任务测试】

1. 如图3-2-41所示，已知F1=-20 kN、F2=8 kN、F3=10 kN，试用截面法求图示杆件指定截面1、2、3的轴力，并画出轴力图。

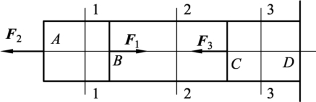
图3-2-41　杆件受力图

2. 如图3-2-42所示，阶梯轴受轴向力F1=25 kN、F2=40 kN、F3=15 kN，截面积A1=A3=400 mm2，A2=250 mm2，请问哪一段截面最先出现断裂失效。

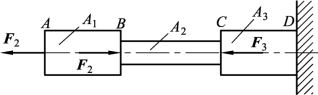
图3-2-42　阶梯轴

3. 某铁路部门检修车间要自制一台简易吊车，如图3-2-43（a）所示，已知在铰接点B处吊起重物的最大值为FP=20 kN，杆AB和BC杆均用圆钢制作，且dBC=20 mm，材料的许用应力[σ]=58 MPa 。试校核BC杆的强度，并确定AB杆的直径d（不计杆自重）。

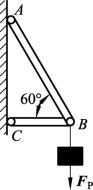
图3-2-43　简易吊车

4. 如图3-2-44所示的直角三角架，AB为圆形截面钢杆，直径d=30 mm，BC为矩形截面木杆，尺寸b=60 mm，h=120 mm。若钢的许用应力为[σ]1=170 MPa，木材的许用应力为[σ]2=10 MPa ，试求该结构的许用载荷F。

图3-2-44　直角三角架

5. 图3-2-45所示为某铁路设备用联轴器，用4个螺栓连接，螺栓对称地安排在直径D=480 mm的圆轴上。已知这个联轴器M=24 kN·m，螺栓材料的许用切应力[]τ=80 MPa。试求螺栓的直径d（其中，假设各螺栓所受的剪力相等）。

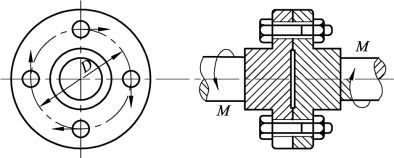
图3-2-45　联轴器

6. 一螺栓连接如图3-2-46所示，已知P=200 kN，δ=20 mm，螺栓材料的许用应力[τ]=80 MPa，试求螺栓的直径。

7. 已知一齿轮轴如图3-2-47所示，主动轮A上输入功率为15 kW，B、C轮为输出轮，输出轮B上输出功率为10 kW，轴的转速为n=1 000 r/min。试求各段轴横截面上的扭矩，并绘出扭矩图。

图3-2-46　螺栓连接

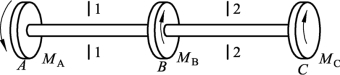
图3-2-47　齿轮轴受力图

8. 如图3-2-48所示，某电机传动轴由45钢制成，已知材料的[]τ=60 MPa，轴传递的功率P=16 kW，转速n=100 r/min，试确定其直径。

9. 简支梁受载荷如图3-2-49所示，试作出该梁的剪力图和弯矩图。

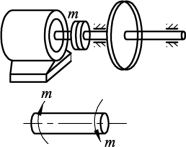
图3-2-48　电机传动轴

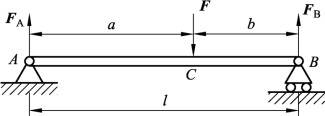
图3-2-49　简支梁

10. 图3-2-50所示的吊车梁由32b工字钢梁制成，梁的跨度l=10 m，梁的材料为A3钢，许用应力[σ]=140 MPa，电葫芦自重G=15 kN，梁自重不计，求该梁能够承担的起重量Q。（32b工字钢的抗弯截面系数WZ =726.3× 103 mm3）

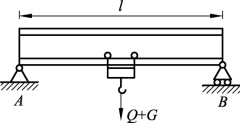
图3-2-50　吊车梁