圆轴扭转的概念与应用

（一）扭转的概念

在杆件两端作用两个大小相等、方向相反且垂直于杆件轴线的力偶，使杆件的任意两个横截面产生绕杆件轴线的相对转动，这种变形称扭转变形。以扭转变形为主要变形的构件称为轴。受扭转圆轴如图3-2-23所示。

图3-2-23　受扭轴实例

（二）圆轴扭转受力和变形的特点

圆轴扭转受到的外力偶矩为M。

1. 扭转变形的受力特点

杆件受力偶系的作用，这些力偶的作用面都垂直于杆轴线。

2. 变形特点

两外力偶作用面之间的各横截面都绕轴线产生相对转动。

（三）外力偶矩

在工程中，作用于圆轴上的外力偶矩一般不是直接给出的，通常给出的是圆轴所需传递的功率和转速。外力偶矩计算公式为

式中 P —— 轴所传递的功率（kW）；

n —— 轴的转速（r/min）。

（四）扭 矩

扭转时的内力偶矩称为扭矩。截面上的扭矩与作用在轴上的外力偶矩组成平衡力系，扭矩求解仍然使用截面法。如图3-2-24所示，由力偶平衡条件可知：m—m截面上必须有一个内力偶矩T与外力偶矩M1平衡。

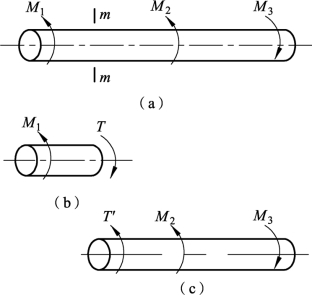
图3-2-24　截面法求扭矩

由∑M=0

得M1-T=0，T=M1。

若取m—m横截面的右端部分为研究对象画出受力图，如图3-2-24（c）所示，可

求得m—m横截面上的扭矩T′。显然，T′与T大小相等，方向相反。

由∑M=0

得T′+M2-M3=0，T′=M3-M2

扭矩符号用右手螺旋法则确定，指向截面外为正，指向截面内为负，右手螺旋法则如图3-2-25所示。

图3-2-25　右手螺旋法则

（五）扭矩图

一般而言，轴各横截面上的扭矩是不相同的。当轴上同时作用两个以上的外力偶矩时，为了形象地表示各截面扭矩的大小和正负，以便分析危险截面，把轴线作为x轴（横坐标轴），以纵坐标轴表示扭矩T，这种用来表示轴横截面上扭矩沿轴线方向变化情况的图形称为扭矩图，如图3-2-26所示。

（六）圆轴扭转时的应力

在小变形的情况下，圆轴扭转时的变形特点如下：

（1）各圆周线的形状大小及圆周线之间的距离均无变化。

（2）各圆周线绕轴线转动了不同的角度。(www.xing528.com)

（3）所有纵向线仍近似为直线，只是同时倾斜了同一角度γ。扭转变形如图3-2-27所示。

图3-2-26　扭矩图

图3-2-27　扭转变形

由扭转变形的特点可以推出结论：

各点切应力的大小与该点到圆心的距离成正比，其分布规律如图3-2-28所示。根据横截面上切应力的分布规律，可由静力平衡条件推导出任意截面上的最大切应力，其计算公式为

式中 PW—— 抗扭截面系数（m3）。

图3-2-28　轴扭转时横截面上的切应力

工程上经常采用的轴有实心圆轴和空心圆轴两种，实心圆轴的抗扭截面系数PW的计算公式为

空心圆轴的抗扭系数PW的计算公式为

式中 d —— 实心轴的直径（m）；

D1—— 空心轴的外径（m）；

D2—— 空心轴的内径，α=D2/D1。

（七）圆轴扭转时的强度条件和应用

为保证圆轴扭转时具有足够的强度而不被破坏，必须限制轴的最大剪应力不得超过材料的许用扭转剪应力。对于等截面圆轴，其最大剪应力发生在扭矩值最大的横截面（危险截面）的外缘处，故圆轴扭转的强度条件为切应力τ不超过材料的许用切应力[τ]，即τmax≤[τ]。应用扭转强度条件，可以解决圆轴强度计算中的三类问题：校核强度、设计截面和确定许可载荷。

对于阶梯轴，由于抗扭截面系数PW不是常量，最大工作应力不一定发生在最大扭矩所在的截面上。因此要综合考虑扭矩和抗扭截面系数PW，由这两个因素来确定最大切应力。

对于等截面圆轴，圆轴扭转的强度条件计算公式为

式中 Tmax—— 最大扭矩（N·m）。

例 3-2-7 一阶梯圆轴如图 3-2-29（a）所示，轴在A、B、C处受到的外力偶矩M1=6 kN·m，M2=4 kN·m，M3=2 kN·m，轴材料的许用切应力[τ]=60 MPa，试校核此轴的强度。

图3-2-29　阶梯圆轴扭矩图

解 （1）绘制扭矩图，如图3-2-29（b）所示。

（2）校核AB段的强度。

（3）校核BC段的强度。

综合（2）、（3）可知，该轴强度足够。