力的平移定理与平面任意力系的平衡

（一）力的平移定理

力的平移就是把作用在刚体上的一力从其原位置平行移到该刚体上另一位置。由力的可传性得知，力沿其作用线移动时，对刚体的作用效果是不改变的。下面研究在不改变力对刚体作用效果的前提下将力平行移动到作用线以外的任意一点这个问题。

如图3-1-39（a）所示，设有一力F作用于刚体的A点，为将该力平移到任意一点O，在O点加一对平衡力F′和F′，作用线与F平行，且使F′=F′=F。其中F和F′两力组成一个力偶，其力偶臂为d。其力偶矩恰好等于原力F对点O之矩M，如图3-1-39（b）所示。这三个力可以转化为一个作用在O点的力F′和一个力偶矩M组成的力系，如图3-1-39（c）所示。

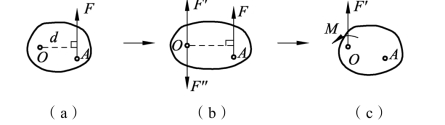
图3-1-39　力的平移

力的平移定理：作用在刚体上某点的力可以平移到刚体上任意一点，平移时需要附加一个力偶，附加力偶的力偶矩等于该力对平移点之矩。

力的平移定理是力系向一点简化的理论依据，也是分析和解决工程实际中力学问题的重要方法。

（二）平面任意力系的简化

工程实践中经常遇到平面任意力系的问题，即作用在物体上力的作用线都分布在同一平面内，或可以简化到同平面内，但它们的作用线任意分布，称为平面任意力系。

要想解决平面任意力系的问题，需要了解平面任意力系的简化方法。

设刚体受一个平面任意力系1F，2F，…，nF的作用，如图3-1-40（a）所示。利用力的平移定理，可将平面任意力系向一点简化，得到作用于点O的n个力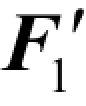、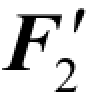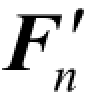，…，的平面汇交力系，以及相应的附加力偶共同作用在同一平面内，这些附加力偶的力偶矩分别为M1，M2，M3，…，Mn，如图3-1-40（b）所示，即一个平面汇交力系和一个平面力偶系。

综上所述，平面任意力系等效为两个简单力系：平面汇交力系和平面力偶系。然后分别合成这两个力系。

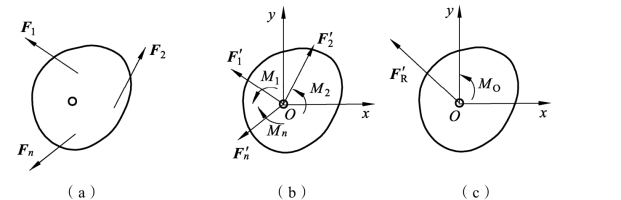
图3-1-40　平面任意力系的简化

（三）平面任意力系的平衡方程

由平面任意力系的简化可知：主矢等于零，表明作用于简化中心的汇交力系为平衡力系；主矩等于零，表明附加力偶系也是平衡力系。

因此平面任意力系平衡的必要和充分条件：力系的主矢与主矩同时等于零，即

平衡条件可用解析式表示为

式（3-1-21）为平面任意力系的平衡方程，由此可得，平面任意力系平衡的条件是力系中各力在两个任选坐标轴上投影的代数和等于零，以及各力对平面内任意点之矩的代数和也等于零。

（四）构件平面任意力系的分析

利用平面任意力系平衡方程求解构件的未知力，要对构件的平面任意力系进行分析，分析方法和步骤如下。

（1）确定研究对象。画出研究对象的受力图，在受力图上确定未知力（约束反力）的数目、作用点位置及作用方向。注意选好坐标轴，坐标轴最好能垂直于一个或两个未知力。一般水平和铅垂方向的坐标轴可以不画，倾斜方向的坐标轴则必须画出。

（2）列平衡方程求解。可按选好的坐标轴列出投影方程，并按选好的矩心列出力矩方程求解。为避免解联立方程，由一个方程解得一个未知力，除选好坐标轴之外，还应注意尽量选择两个未知力的交点为矩心。

例3-1-9 如图3-1-41（a）所示，水平梁受载荷F=60 kN，均布载荷q=20 kN/m，梁的自重不计，试求A、B处的支座约束力。

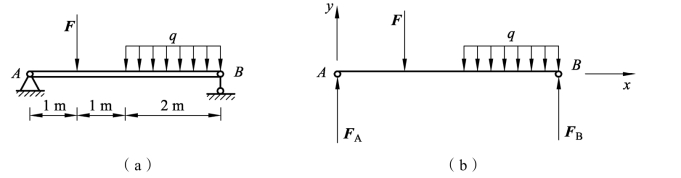
图3-1-41　水平梁受力图

解 （1）选取研究对象。取梁AB为研究对象。

（2）进行受力分析并画受力图。梁上作用竖直向下的载荷F、q和活动铰链B处竖直向上支座约束力FB，要保证力系为平衡力系，固定铰链A处支座约束反力FA必为竖直方向。受力如图3-1-41（b）所示。

（3）以A为原点，建立坐标系，如图3-1-41（b），列平衡方程如下

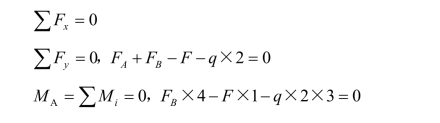
解得FA=55 kN，FB=45 kN。

通过对本任务的学习，你会画图3-1-1中内燃发动机活塞的受力图了吗？如果已知约束反力FR和FN，你知道用什么方法求解主动力F吗？

例3-1-10 某送料小车如图3-1-42（a）所示，车和货物共重G=240 kN，重心在C点。已知：a=1 m，b=1.4 m，e=1 m，h=1.4 m，α=30°。如不考虑小车与轨道之间的摩擦，求钢索的拉力和轨道的支反力。

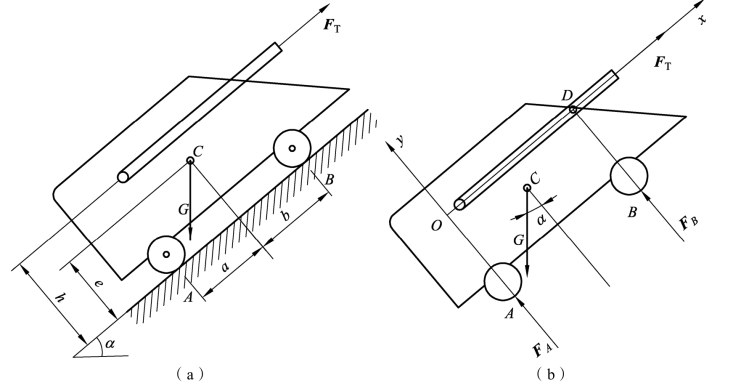
图3-1-42　送料小车

解 （1）取小车为研究对象，画受力图并选取坐标系Oxy，取O点为简化中心，受力如图3-1-42（b）所示。

（2）列平衡方程求解。

解得FT=120 kN(www.xing528.com)

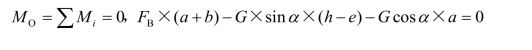
解得FB=106.6 kN

解得FA=101.2 kN

【思考】

从作用力和反作用力、约束力和反约束力的关系，对你进入社会后应该怎样与他人相处有什么启示吗？

【实践操作】

如图3-1-43（a）所示，对水平放置的工件进行钻孔。3个钻头对工件施加的力偶矩分别为M1=M2=10 N·m，M3=20 N·m，固定螺栓A和B的距离l=200 mm。请画出该工件的受力图，并求出两个螺栓所受的力。

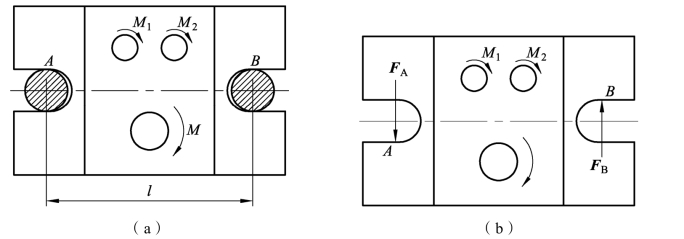
图3-1-43　工件钻孔

【任务测评】

1. 水平梁AB左端为固定铰支座，右端为活动铰支座，如图3-1-44所示，假设不计构件的重量，AB杆上作用主动力Q、P，试画出其受力图。

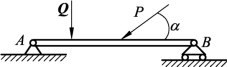
图3-1-44　水平梁

2. 如图3-1-45所示的平面系统中，均质球A重为P，借本身重量和摩擦不计的理想滑轮C和柔绳维持在仰角为α的光滑斜面上，绳的一端挂着重为Q的物体B。试分析物体B、球A和滑轮C的受力情况，并分别画出平衡时各物体的受力图。

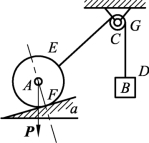
图3-1-45　滑轮机构

3. 如图3-1-46所示，等腰三角形构架ABC的顶点A、B、C都用铰链连接，底边AC固定，而AB边的中点D作用有平行于固定边AC的力F，如下图所示。不计各杆自重，试画出AB和BC的受力图。

4. 如图3-1-47所示，水平均质梁AB重为1P，电动机重为2P，不计杆CD的自重，画出杆CD和梁AB的受力图。

图3-1-46　等腰三角形构架

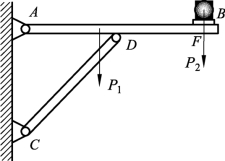
图3-1-47　水平均质梁

5. 如图3-1-48所示，刚架上作用力F=100 N，角θ=60 °，a=6 m，b=4 m。试分别计算力F对点A和B的力矩。

6. 铁道机车车辆某铆接薄板在孔心A、B和C处受3个力作用，如图3-1-49所示。F1=100 N，沿铅直方向；F3=50 N，沿水平方向，并通过点A；F2=50 N，力的作用线也通过点A，其他尺寸如图3-1-49所示。求此力系的合力。

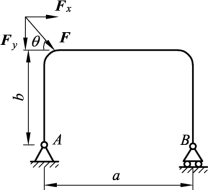
图3-1-48　受力刚架

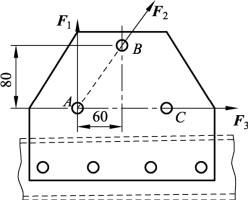
图3-1-49　铆接薄板

7. 简易起重装置如图3-1-50所示，重物用钢丝绳挂在支架的滑轮B上，钢丝绳的另一端缠绕在绞车C上。杆AB与杆BD铰接，并且铰链A、D与墙连接。设重物重力G=50 kN，两杆和滑轮的自重不计，并忽略摩擦和滑轮的大小，试求平衡时杆AB和杆BD所受的力。

8. AB杆的A端为固定铰支座约束，B端为活动铰支座约束，在杆的C处作用一集中力P=10 N，α=45°，杆的尺寸如图3-1-51所示，假设杆的自重忽略不计，试求各支座的约束力。

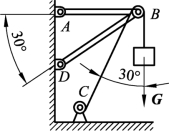
图3-1-50　简易起重装置图

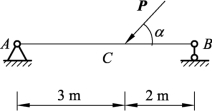
图3-1-51　简支梁

9. 钢筋混凝土刚架的受力及支座情况如图3-1-52所示。已知F=50 N，M=90 N·m，点A、B距离为4 m，刚架高为6 m，刚架自重不计，求支座约束力。

10. 求图3-1-53所示组合梁A、B、C处的约束反力。

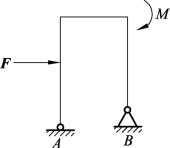
图3-1-52　钢筋混凝土刚架

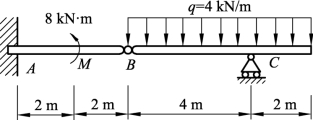
图3-1-53　组合梁