平衡定理之力矩、力偶和平面力偶系

（一）力矩与合力矩

1. 力 矩

实践表明，作用在刚体上的力除有平动效应外[图3-1-31（a）]，有时还有转动效应[图3-1-31（b）、（c）]，力对刚体的转动效应可用力矩来度量。

图3-1-31　力对物体的作用效应

如图3-1-32所示，用扳手拧螺母使螺母产生绕O点转动的力矩，不仅与力F的大小有关，与O点至该力作用线的垂直距离d也有关。点O称为矩心，点O到力的作用线的垂直距离d称为力臂。力的大小与力臂的乘积，称为力矩，即

式中 MO(F)—— 力对O点之矩（N·m或kN·m）；

F —— 作用力（N或kN）；

d —— 力臂（m或mm）。

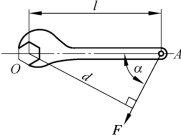
图3-1-32　扳手拧螺母

力矩的正负值代表了物体的转动方向，通常规定力使物体绕矩心沿逆时针方向转动为正，反之为负。

2. 合力矩定理

平面汇交力系的合力对平面内任一点的矩，等于力系中各分力对该点力的矩的代数和。即

例3-1-6 如图3-1-33所示，已知两齿轮齿面之间的啮合力为P，其作用线与齿轮节圆切线方向的夹角为α（压力角），节圆直径为d。求啮合力P对轮心O点之矩。

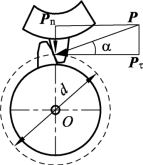
图3-1-33　齿轮传动受力图

解 两齿轮齿面之间的啮合力P可分解为两个分力τP和nP，

利用合力矩定理：

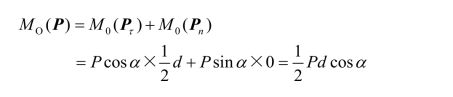
（二）力偶与力偶矩

1. 力 偶

在实践中，我们常常见到汽车司机用双手转动方向盘，钳工用丝锥攻螺纹，拧水龙头（图3-1-34）。这种由两个大小相等、方向相反、作用线不重合的平行力组成的力系称为力偶，记作（F、F′），如图3-1-35所示。力偶的两个力之间的垂直距离d称为力偶臂。力偶所在的平面称为力偶的作用面。力偶对物体的作用效应是使物体产生转动运动。

图3-1-34　生活中的力偶

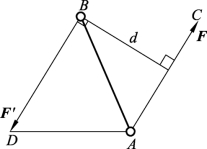
图3-1-35　力偶

2. 力偶矩

力偶对物体的转动效应，可用力偶矩来度量，力偶矩的大小为力偶中的两个平行力对其作用面内某点之矩的代数和，其值等于力与力偶臂的乘积Fd，记作M（F，F′）或M，即

一般在同一平面内，逆时针方向转动的力偶矩为正，顺时针方向转动的力偶矩为负。

力偶矩的单位符号与力矩相同，即N·m或kN·m。

3. 力偶的性质

力偶是两个特殊的有关联的力组成的，因此具有与单个力所不同的性质。

性质1 力偶无合力，因此力偶不能与一个力等效，也不能用一个力来平衡。力与力偶之间不能相互代替，不能相互平衡。故力和力偶是力学中的两种基本元素。

性质2 力偶对其作用面内任意一点之矩的代数和恒等于力偶矩，而与矩心的位置无关。

如图3-1-36所示，在力偶（F，F′）所在的平面内，任取一点O为F、F′两力的转动中心，根据合力矩定理，有

由于矩心的位置是任取的，因此，力偶矩与矩心位置无关。

性质3 平面力偶等效定理：同一平面内的两个力偶等效的充分必要条件是其力偶矩相等。(www.xing528.com)

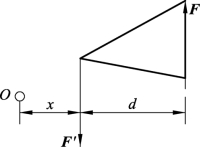
图3-1-36　力偶与矩心

（三）平面力偶系的合成与平衡方程

1. 平面力偶系的合成

作用在物体同一平面内有多个力偶，称为平面力偶系。平面力偶系可以合成为一个合力偶。设M1，M2，…，Mn为平面力偶系中各力偶的力偶矩，Mi为合力的合力偶矩，它等于各力偶矩的代数和，即

2. 平面力偶系的平衡

由合成结果可知，力偶系平衡时，其合力偶矩等于零。因此，平面力偶系平衡的必要和充分条件是平面力偶系中各分力偶矩的代数和等于零，即

即式（3-1-17）为平面力偶系的平衡方程。

（四）构件平面力偶系的分析

用平面力偶系平衡方程来求解构件平衡问题，首先要对构件进行受力分析，其分析方法同平面汇交力系。具体步骤为选择研究对象，取分离体并画受力图，根据平面力偶系平衡方程求解未知量。

若求出的力偶为正值，则表示受力图上假设力偶的方向与实际方向相同；若求出的力偶为负值，则表示受力图上力偶的假设方向与实际方向相反，在受力图上不必改正，在答案中要说明。

例3-1-7 如图3-1-37（a）所示，一简支梁作用的力矩M=50 N·m，简支梁长d=4 m，不计梁重，求支座A和B的约束反力。

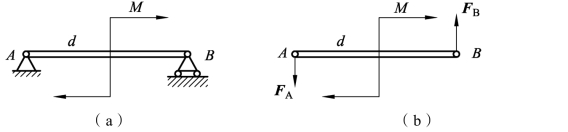
图3-1-37　简支梁受力分析

解 （1）选择研究对象，以梁AB为研究对象。

（2）进行受力分析并画受力图。由于AB梁自重不计，梁A端为固定铰链，梁B端为活动铰链。梁上除作用有力偶M外，还有固定铰链A处的约束反力FA及活动铰链B处垂直向上的约束反力FB。根据力偶只能与力偶相平衡的性质，可知FA和FB必组成一个力偶，因此，FA的作用线也沿铅垂方向，如图3-1-37（b）所示。

（3）列平衡方程，求出未知力。梁AB在两个力偶的作用下处于平衡，根据平面力偶系的平衡条件列平衡方程如下

解得

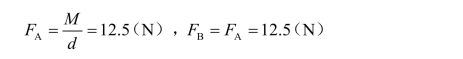
FA和FB的计算值为正值，其实际方向如图3-1-37（b）所示。

例3-1-8 如图3-1-38（a）所示，四杆机构在图示位置平衡，已知lOA=20 cm，l 1O B=40 cm，作用在曲柄OA上的力偶矩为M1=2 N·m，不计杆重，求作用在杆O1B上的力偶矩M2的大小及连杆AB所受的力。

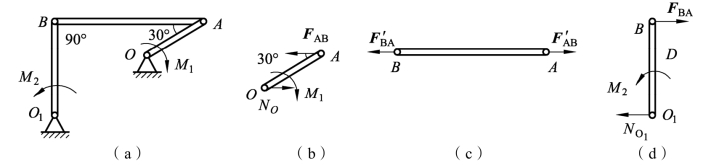
图3-1-38　四杆机构受力分析

解 （1）选择研究对象。根据题目要求，分别选OA、AB、O1B为研究对象。

（2）进行受力分析并画受力图。

以OA杆为研究对象：OA杆受到力偶矩M1、二力杆AB对其的反作用力FAB，以及铰链O处的约束反力NO的作用，根据平面力偶系的平衡条件，FAB和NO组成一个力偶，受力如图3-1-38（b）所示。

以AB杆为研究对象：AB杆为二力杆，受力分析如图3-1-38（c）所示。

以O1B杆为研究对象：根据平面力偶系的平衡条件，FBA和N1O组成了一个力偶，受力分析如图3-1-38（d）所示。

（3）列平衡方程，求出未知力

OA杆：根据平面力偶系的平衡条件，列平衡方程如下

解得

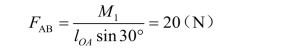
AB杆：根据二力平衡和作用力与反作用力公理，列平衡方程如下

O1B杆：根据平面力偶系的平衡条件，列平衡方程如下

解得