静力学的基本概念和公理简介

（一）力

1. 力的定义

力的概念是人们在长期生产劳动和生活实践中逐渐建立起来的，如推车（图3-1-2）、吊车梁（图3-1-3）等的使用，都要用力；在图3-0-1中的铁路车辆轮对受到车辆的重力、牵引力、制动力；图3-0-2中的铁路车辆半永久牵引杆受到牵引力和冲击力。

图3-1-2　推车

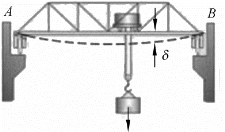
图3-1-3　吊车梁

力是物体间的相互机械作用，这种作用可以使物体的运动状态发生变化或使物体产生变形。使物体的运动状态发生变化的效应称为力的外效应，使物体产生变形的效应称为力的内效应。

在工程实践中，力作用于物体，总会引起物体的变形。当变形很小，在研究物体的外效应时，常常忽略物体的变形，把物体视为刚体（受力后其几何形状和尺寸保持不变的物体），这样可以使问题研究简单化。

2. 力的三要素

力对物体的作用效果取决于力的大小、方向和作用点，这三个因素称为力的三要素。

（1）力的大小。力的大小表示物体之间机械作用的强度。在国际单位制中，力的单位为牛顿，符号为N。工程中常用千牛顿作为单位，符号为kN，1 kN=1 000 N。

（2）力的方向。力的方向表示物体之间机械作用的方向，包含力的方位和指向两个方面的含义。

（3）力的作用点。力的作用点是物体受到机械作用的位置。力的作用位置实际上有一定的范围，当作用范围与物体相比很小时，可以近似地看作一个点。

根据受力特点，力可以分为集中力和均布力。其中，集中力的作用点为一个点，均布力的作用点为线或者面。

3. 力的表示方法

力的三要素可用带箭头的有向线段（矢线）标于物体作用点上：线段的长度（按一定比例画出）表示力的大小，箭头的指向表示力的方向；线段的起始点或终止点表示力的作用点；通过力的作用点，沿力的方向的直线，叫作力的作用线。

力可以用F或P等字母表示，如图3-1-4所示。

均布载荷一般用q来表示，如图3-1-5所示。

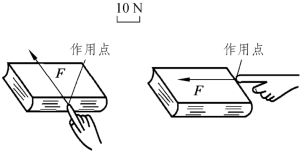
图3-1-4　集中力的表示方法

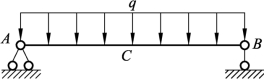
图3-1-5　均布力的表示方法

均匀载荷的作用效果是可以转换成集中载荷的。由于结构特点、边界条件的不同，将均布载荷转换为集中载荷不可能有统一的计算公式，但有三个基本原则：

（1）载荷位置相同。均布载荷的合力点就是集中载荷的作用点。

（2）总值相同。均布载荷总的载荷值就是集中载荷的载荷值。

（3）误差最小。简化模型力求误差最小。

（二）力 系

1. 力系的定义

力系是指作用于物体上的一群力。当物体只有一个力作用时，即为最简单的力系。

2. 等效力系

如果一个力系与另一个力系对物体的作用效应相同，则这两个力系互为等效力系。可以用一个简单力系等效代替一个复杂力系，从而使问题简化。

3. 平衡力系

如果某一个力系作用到原来平衡的物体上，而物体仍然保持平衡，则此力系为平衡力系。

4. 合力与分力

如果一个力与一个力系等效，则称此力为该力系的合力，该力系中各力称为该合力的分力。由已知力系求合力的过程称为力系的合成，反之为力的分解。

5. 力系的分类

力系按照作用线是否处于同一平面可以分为两种，即平面力系和空间力系。本书只介绍平面力系。所有力的作用线在同一平面内的力系为平面力系，平面力系又可分为以下三种：

（1）平面汇交力系：所有力的作用线汇交于一点的平面力系，如图3-1-6（a）所示。

（2）平面平行力系：所有力的作用线都相互平行的平面力系，如图3-1-6（b）所示。

（3）平面任意力系：所有力的作用线既不汇交于同一点，又不相互平行的平面力系，如图3-1-6（c）所示。

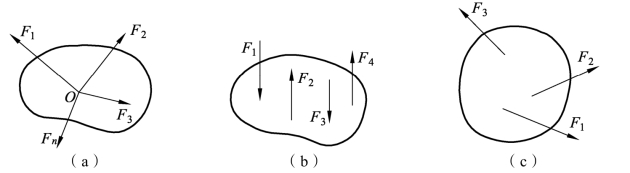
图3-1-6　平面力系

（三）静力学公理(www.xing528.com)

1. 力的平行四边形法则

作用于物体上同一点的两个力可以合成为一个合力。其合力仍作用于该点上，合力的大小和方向由以这两个力为邻边所构成的平行四边形的对角线来确定。

如图3-1-7所示，1F、2F为作用于O点的两个力，以这两个力为邻边作出平行四边形OACB，则对角线OC即为1F与2F的合力RF，或者说合力RF等于原力1F与2F的矢量和，即

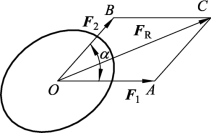
图3-1-7　力的平行四边形法则

合力的大小可由余弦定理求出，即

式中 α ——1F与2F的夹角（°）。

实际上，根据平行四边形的性质，确定作用于一点的两个力的合力时，并没有必要一定要作一个平行四边形，只要不改变这两个力的大小和方向，将它们首尾相接，则合力始于它们的起点，而止于它们的终点，如图3-1-8所示，这种求合力的方法称为力的三角形法则。

依据力的平行四边形法则可将一个力分解成作用于同一点的两个分力。一个力可以沿任意两个方向分解。在工程问题中，常将力沿互相垂直的两个方向分解，这种分解称为正交分解。

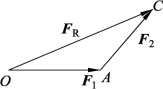
图3-1-8　力的三角形法则

2. 二力平衡公理

平衡是指物体相对惯性参考系处于静止或匀速直线运动状态。

作用在刚体上的两个力使刚体处于平衡状态的必要和充分条件：两个力的大小相等，方向相反，作用在同一直线上，如图3-1-9所示，即

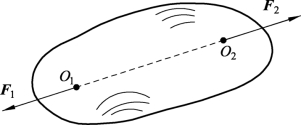
图3-1-9　二力平衡

工程上将只受到两个力作用且处于平衡状态的构件称为二力构件。如图3-1-10所示，直杆AB和曲杆AC都是二力构件。

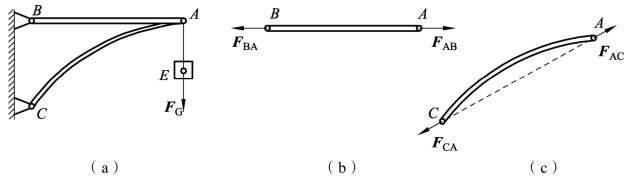
图3-1-10　二力构件

3. 加减平衡力系公理

在作用于刚体的任意力系上加上或减去任意平衡力系，并不改变原力系对刚体的作用效果。加减平衡力系原理只适用于刚体，而不能用于变形体。

推论1 力的可传性

作用于刚体上某点的力，可以沿着它的作用线移到刚体内任意一点，并不改变该力对刚体的作用。

证明 设在刚体上A点有作用力F，如图3-1-11（a）所示。

根据加减平衡力系公理，可在力的作用线上任取一点B，并加上两个相互平衡的力F1和F2，使F2=-F1 =F，如图3-1-11（b）所示。

由于F和F1也是一个平衡力系，故可除去，这样只剩下一个力F2，如图3-1-11（c）所示。原来的这个力F与力系（F、F1、F2）以及力F2互等，F2就是原来的力F，只是作用点已移到了点B。

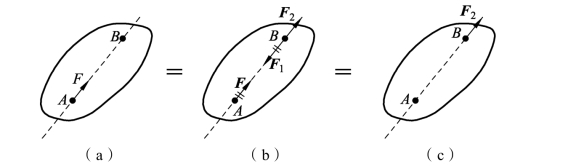
图3-1-11　力的可传性原理

由此可见，对于刚体来说，力的作用点已不是决定力的作用效果的要素，它被作用线所代替。因此，作用于刚体上的力的三要素是力的大小、方向和作用线。

推论2 三力平衡汇交定理

刚体在三个力的作用下平衡，若其中两个力的作用线相交，则第三个力的作用线必过该交点，且三力共面。

证明 如图3-1-12所示，刚体上A、B、C三点上的作用力分别为1F、2F和3F，其中，1F与2F的作用线相交于O点，刚体在此三力作用下处于平衡状态。根据力的可传性原理，将1F和2F合成得合力F12，则力3F应与F12平衡，因而3F必与F12共线，即3F作用线也通过O点。另外，因为1F、2F与F12共面，所以1F、2F与3F也共面。该定理得证。

利用三力平衡汇交定理可以确定刚体在三力作用下平衡时未知力的方向。

4. 作用与反作用公理

一个物体受到其他物体作用时，施力物体一定也受到与受力物体等值反向的力的作用，这两个力互为作用力和反作用力。两物体间的作用力与反作用力总是同时存在，且两者大小相等、方向相反、沿同一直线，分别作用在相互作用的两个物体上。

注意：作用力与反作用力是分别作用在两个物体上的力，因此不能将它们看作平衡力而互相抵消。如图3-1-13所示，重物对桌子的压力N′和桌子对重物的支持力N作用在两个不同的物体上，互为作用力和反作用力，桌子对重物的支持力N与重物的重力G两者为平衡力。

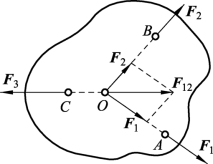
图3-1-12　三力平衡汇交定理

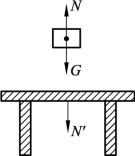
图3-1-13　作用力与反作用力