改进趋势法优化策略解析

改进趋势法主要用于预测中短期空间负荷预测。为了与实际情况保持一致，采用了不规则分区的划分方法，即在对现状及发展规划进行详细研究的基础上，根据各个负荷的实际位置与范围对规划用地进行划分，进而确定各地块负荷值的大小，这相当于把总负荷分配到其所对应的各块用地中去。由于不同地域的发展状况不同而存在用电的不均衡性，即相同面积的两块用地所对应的负荷值不一定相同，并且随着时间的推移，各地块负荷的发展情况不同。一般条件下，负荷密度较高的区域其负荷的发展速度相应减缓，负荷密度较低的区域其负荷的发展速度相应较快；再者，对于某类负荷而言，其单位建筑面积所需负荷值应该存在一个上限，也即存在一个饱和值。由此，若仅根据负荷的平均密度，按规划区各用地上建筑面积的大小来分配负荷，所得到的负荷分布结果肯定与实际情况不符，将使某些面积大而当前负荷较低的地块其未来负荷的计算值依然很低，而使一些初始负荷密度较大的区域随着时间增长而达到一个高得令人难以置信的地步。

改进趋势法的本质是：假定同类小区负荷都按照相同的S型曲线增长，根据各小区当前的负荷密度确定该小区的增长率后，将分类负荷增长量分配到各个小区，得到小区的未来负荷。

改进趋势法特别适用于发展比较成熟或正在发展的小区。对于新建区或还没有发展的小区，负荷密度接近零时，预测时难以确定该小区负荷发展所处的位置，因此，预测会出现一定的偏差。

为了突出主要矛盾，从而利用数学模型对负荷发展情况加以分析，改进趋势法从实际出发作出三点假设：

（1）对于一类负荷，其不同地域处的负荷密度可以不同，但它们的发展趋势相同，即不同地块处的负荷密度都遵循同样的发展曲线变化，这条曲线是由这类负荷本身的性质决定的，而各地块处的密度差异只是因为它们处于该曲线上的位置不同，高负荷密度意味着处于负荷发展曲线的较高阶段，低负荷密度意味着处于该曲线的较低阶段。

（2）对于任一类负荷其密度都存在一饱和值，即存在常数。为某负荷类别的单位面积负荷上限。该数与该类负荷性质有关，可参照发达地区的同类负荷相应数据而得。

（3）该曲线是“S”型曲线，其方程近似为（作者选择该曲线是因为它较好地反映了大部分负荷的发展状况，其实这并不是唯一的曲线，根据负荷性质的不同可以反映为不同的曲线形式，相应有不同的负荷发展方式）。

对负荷密度变化趋势“S”曲线分析可知：

即负荷密度的发展与负荷密度的当前值有关。由假设（1）可得，在同样的时间间隔下，即在dx一定的条件下，i地块与j地块处负荷密度增量的比值：

下面以某一类负荷为例介绍考虑各地块负荷发展不均衡性时的负荷分布确定方法。令：

S为该类的负荷总值；ai为该类第i块用地的面积；ri为该类第i块用地的容积率；wi为该类第i块用地的负荷不均衡调整系数；εi为该类第i块用地的实际单位建筑面积负荷；

则airi为第i块用地上的建筑面积。

令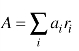为该类负荷的总建筑面积，则为该类负荷的平均单位建筑面积负荷。

引入wi是为了描述不同用地间实际负荷密度的差别，它与εi间的关系如下式：

令Li表示该类第i块用地的负荷值，则：

再由，得，即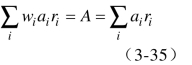　

由式（3-33）可得：

根据假设（3-34）可得：

其中：β是与各用地负荷无关的比例系数，它与规划阶段的时间间隔大小有关。式（3-37）实际上是反映总负荷增量在各用地之间的分配方式，即对于不同地块处的负荷，相应于同一时间间隔，由于处在负荷密度发展曲线上不同的位置而反映为不同的增长速度。

考虑逐年的负荷变化情况，此时由于∆εi、∆wi、∆S、∆A相对并不很大，所以可以认为式（3-36）和式（3-37）为等式，则有：(www.xing528.com)

得

且由式（3-35）可得：

即：

化简得：

注意，在式（3-37），式（3-38）和式（3-40）中仅∆wi， ∆εi，β 是未知量，同该三式即可得到求解逐年εi的迭代过程。

设第k年的wi，S，A，εi，airi皆已知为　，S（k），A（k），，（airi）（k），而∆S（k）a可通过逐年的分类总电量与负荷预测得到∆S（k）=S（k+1）-S（k），∆A（k）与∆（airi）（k）都是反映城市用地变化情况的基础数据，一般由城市规划部门提供或通过逐年用地调查得到。

∆A(k)=∆A(k+1)-A(k)

∆(airi)(k)=(airi)(k+1)−(airi)(k)a

则有：

和

由式（3-41）、式（3-42）得：

代入式（3-41）即可求得　，代入式（3-37）即可求得，则：

而负荷值：

由此，即可求得第k+1年各用地处的负荷值。

关于初值，的选择可如下处理。

设第i块用地的负荷当前值为，则由：

得：

利用以上的计算过程即可以求得各个负荷用地处的逐年负荷值，并且能很好地与实际相符。注意，这一过程主要适用于自然增长的负荷形式，对于某阶段一些用地由于投运新建设项目而阶跃形增长的负荷情况，可以考虑为在该用地处新加一点负荷，再对点负荷单独计算其增长过程，若项目的用地与负荷数据可知，还可以用该阶段的数据对原计算数据进行修正，作为下一阶段的新的初始值而用同样的方法计算负荷发展情况。对由于用地性质变化而引起的负荷变化也可类似处理。

改进趋势方法有效地解决了规划进程中，各地块处负荷发展的不均衡性问题，实用效果良好。