农村电力需求的增长受到经济发展、产业结构、居民收入水平、气候、国家政策（电价）等诸多因素的影响，其中一些因素是确定的，而另一些因素是不确定的，因此农村电力的年需求量变化很大。如表3-5所示的某县1996～2006年电力消费量表明，该数据系列呈上升的趋势性，同时又具有较大的波动性，因而可用灰色—马尔柯夫预测法进行预测和分析。
表3-5 某县历年电力总消费量 单位：万kW·h
1. 建立GM（1，1）模型
并利用GM（1，1）模型求出2006年的农村电力需求量预测值为：390695.63096×104kW·h。
2. 划分状态区间
以
作为基准线，再根据农村电力需求量的历史数据情况，并考虑到计算的方便性，划分成如下四个状态区间：
其中：
为历年电力消费量的年平均值，
=148458.7×104kW·h。
将观测数据、趋势曲线和划分的四个状态区间表示如图3-1所示。由图3-1可看出，上述状态划分形成了四个与趋势曲线平行的条形区域。
图3-1 历年农村电力需求量预测曲线
3. 计算状态转移概率
根据划分的状态，考查各原始数据可得：
M1=1；M2=3；M3=4；M4＝1(www.xing528.com)
Mi为处于状态Ei的原始数据样本数（i=1～4）。由状态E1一步转移到状态E1，E2，E3，E4的原始数据样本数分别为 M11（1）=0，M12（1）=0，M13（1）=1，M14（1）=0。同样可计算Mij（1）（i=2，3，4；j=1，2，3，4）的值。则由（3-19）式可计算各状态间的一步转移概率Pij（1）（i，j=1，2，3，4）。并构成状态转移概率矩阵如下：
根据以上矩阵可预测农村电力需求量的未来转移状态。由于2005年的实际用电量落在第三区间，而P31=P32=P34，因此还要看第三区间的二次转移概率：
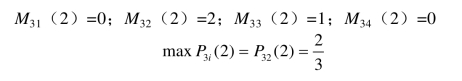
因此，2006年农村电力需求量的预测值最可能落在第二区间。
4. 计算预测值
由式（3-21），可以计算2006年农村电力需求量最可能的预测值（单位：×104kW·h）为：
5. 灰色—马尔柯夫法与灰色GM（1，1）模型预测精度的比较
利用表3-6的数据，采用灰色GM（1，1）模型建立预测模型进行预测分析比较，两种预测方法对农村电力需求量的预测结果如表3-6所示。由表3-6可知，灰色—马尔柯夫预测法的精度比较高。
表3-6 两种预测方法预测结果的比较分析 单位：万kW·h
（1）灰色—马尔柯夫预测法能充分利用时间序列数据给予的信息进行分析预测，与其他常用的时间序列预测方法比较，该方法具有计算简便，精度高的特点。
（2）该法的预测精度，与状态划分的关系较大，但状态划分尚无统一标准，需视历史数据列和研究的具体要求而定。一般历史数据较少时，宜将状态区域划分得大一些，状态数目少一些；而历史数据较多时，则可增加状态数目，将状态区域划分得小一些。这样更能客观地反映状态之间的转移规律。
（3）农村电力需求因受社会、经济、技术、和自然条件的影响，其数据序列往往呈现一定的趋势性和较大的波动性，因而，采用灰色—马尔柯夫预测法预测农村电力需求是比较合适的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
