地图坐标系与投影介绍

首先简单介绍一下地理坐标系、投影坐标系以及地图投影的概念：

地理坐标系为球面坐标，参考平面是椭球面，坐标表示为经纬度；

投影坐标系为平面坐标，参考平面是水平面，坐标单位为米、千米等；

地图投影是将地理坐标转换到投影坐标的过程，即将不规则的地球曲面转换为平面的工作。

1.坐标系

一个完整的坐标系统是由坐标系和基准两个方面要素所构成的。坐标系指的是描述空间位置的表达形式，而基准指的是为描述空间位置而定义的一系列点线面。在大地测量中的基准一般是指为确定点在空间中的位置，而采用的地球椭球或参考椭球的几何参数和物理参数，及其在空间的定位、定向方式，以及在描述空间位置时所采用的单位长度的定义。

理解地理坐标系之前，首先要了解对不规则的抽象即地球空间模型（见图2-3）。地球是一个不规则的球形，自然表面是崎岖不平的，地理课本中对地球形状的描述：地球是一个两极稍扁，赤道略鼓的不规则球体。不难看出在地球的自然状态下，其表面并不是连续不断的，高山、悬崖的存在使得地球表面存在无数的凸起和凹陷。因此，对地球表面的第一层抽象——大地水准面，即得到了一个连续、闭合的地球表面。大地水准面的定义是：假设当海水处于完全静止的平衡状态时，从海平面延伸到所有大陆下部，而与地球重力方向处处正交的一个连续、闭合的曲面，这就是大地水准面，它是重力等位面。在大地水准面的基础上可以建立地球椭球模型。大地水准面虽然十分复杂，但从整体来看，起伏是微小的，且形状接近一个扁率极小的椭圆绕短轴旋转所形成的规则椭球体，这个椭球体称为地球椭球体。其表面是一个规则数学表面，可用数学公式表达，所以在测量和制图中用它替代地球的自然表面，地球椭球体有3个参数：长半轴、短半轴和扁率（见图2-4）。

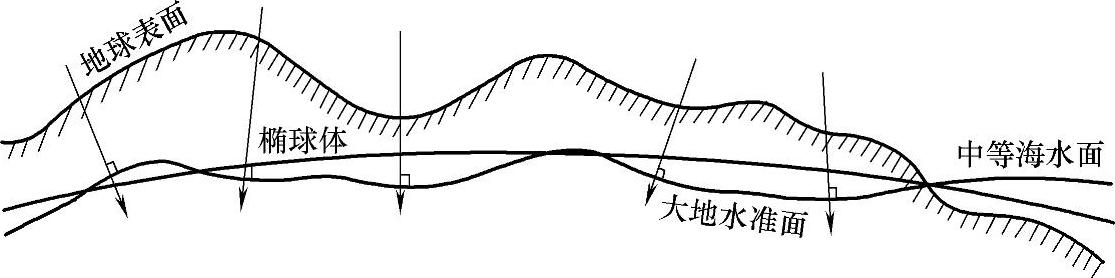
图2-3 地球空间模型示意图

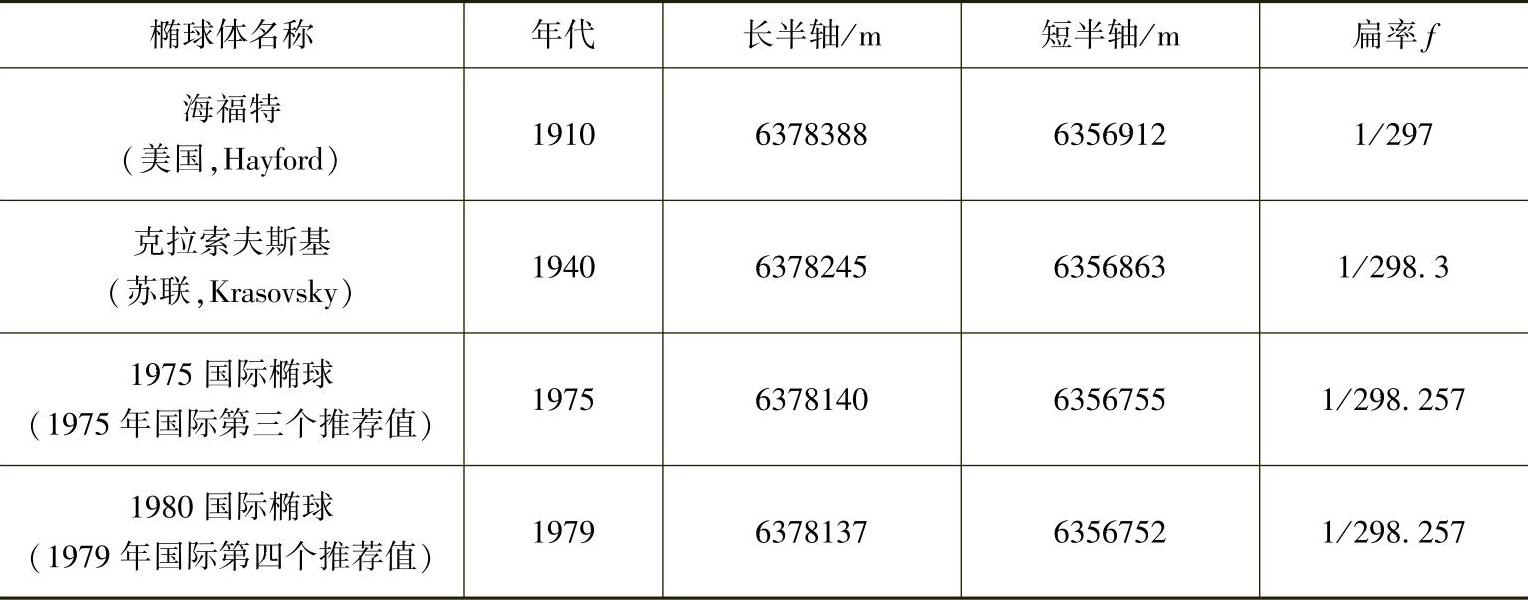
接下来介绍一些常用的参考椭球体，见表2-1。我国在1952年以前采用海福特椭球体，从1953年起采用克拉索夫斯基（Krasovsky）椭球体，我国1954年北京坐标系（BeiJing54）采用的就是该椭球。1978年我国决定采用新椭球体GRS（1975），并以此建立了我国新的、独立的大地坐标系——1980西安坐标系（Xian80）。

有了参考椭球体就可以建立地理坐标系了，但是这里存在一个问题，参考椭球体是对地球的抽象，因此其并不能与地球表面完全重合。在设置参考椭球体的时候必然会出现有的地方拟合得好（参考椭球体与地球表面位置接近），有的地方拟合得不好的问题，因此这里还需要一个大地基准面（Geodetic Datum）来控制参考椭球和地球的相对位置。

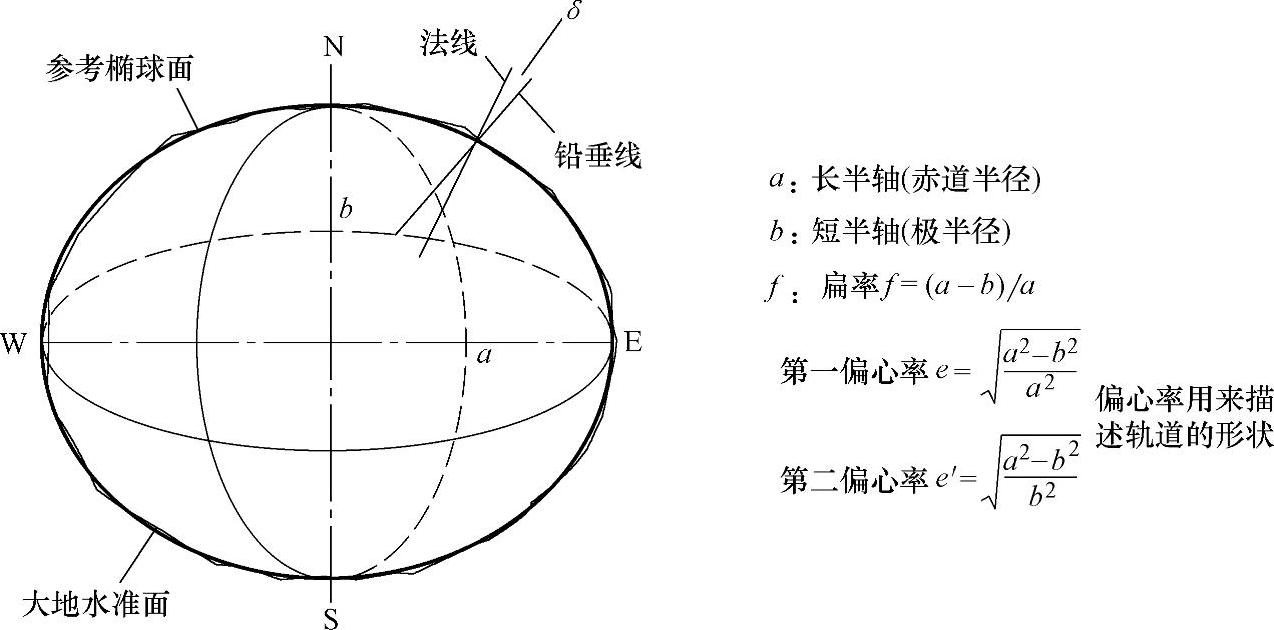
图2-4 地球椭球表示方法

表2-1 我国历史沿用椭球参数表

大地基准面根据原点设置的不同分为以下两类：

•地心基准面：由卫星数据得到，使用地球的质心作为原点，使用最广泛的是WGS84。

•区域基准面（参心基准面）：特定区域内与地球表面吻合，大地原点是参考椭球与大地水准面相切的点，例如BeiJing54、Xian80。每个国家或地区均有各自的大地基准面。我们通常称谓的BeiJing54、Xian80坐标系实际上指的是我国的两个大地基准面。相对同一地理位置，不同的大地基准面，其经纬度坐标是有差异的。椭球体与大地基准面之间的关系是一对多的关系，因为基准面是在椭球体的基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面。

地球椭球体和大地基准面确定完之后，就可以定义坐标系了。大地坐标系可分为参心大地坐标系和地心大地坐标系。

•参心大地坐标系：指经过定位与定向后，地球椭球的中心不与地球质心重合而是接近地球质心。区域性大地坐标系是我国基本测图和常规大地测量的基础，如BeiJing54、Xian80。

•地心大地坐标系：指经过定位与定向后，地球椭球的中心与地球质心重合，如CGCS2000、WGS84。

2.地图投影

地球椭球体为一不可展曲面，地理坐标为球面坐标，不方便进行距离、方位、面积等参数的量算；而我们常用的地图为平面表达，符合视觉心理，并易于进行距离、方位、面积等量算和各种空间分析。

将地球椭球面上的点映射到平面上的方法，称为地图投影。从地理坐标到投影坐标是将不规则的球面展开为平面的过程，因此也是一个将曲面拉平的过程。从生活经验中可以看出这是一个无法精确处理的问题（例如，在剥橘子的时候，如果不破坏橘子皮是无法从原来的“曲面”展开为平面的），要把这样一个曲面表现到平面上，就会发生裂隙或褶皱。在投影面上，可运用经纬线的“拉伸”或“压缩”（通过数学手段）来加以避免，以便形成一幅完整的地图。但不可避免会产生变形，这便涉及了投影方法的问题。

地图投影的变形通常有长度变形、面积变形和角度变形。在实际应用中，根据使用地图的目的，限定某种变形。

地图学中将地图投影按变形性质分为

•等角投影：角度变形为零；

•等积投影：面积变形为零；

•任意投影：长度、角度和面积都存在变形。

其中，各种变形相互联系相互影响：等积投影与等角投影互斥，等积投影角度变形大，等角投影面积变形大。

地图学中将地图投影按投影面类型分为

•横圆柱投影：投影面为横圆柱；(www.xing528.com)

•圆锥投影：投影面为圆锥；

•方位投影：投影面为平面。

地图学中将地图投影按投影面与地球位置关系分为

•正轴投影：投影面中心轴与地轴相互重合；

•斜轴投影：投影面中心轴与地轴斜向相交；

•横轴投影：投影面中心轴与地轴相互垂直；

•相切投影：投影面与椭球体相切；

•相割投影：投影面与椭球体相割。

各种投影方式示意如图2-5所示。

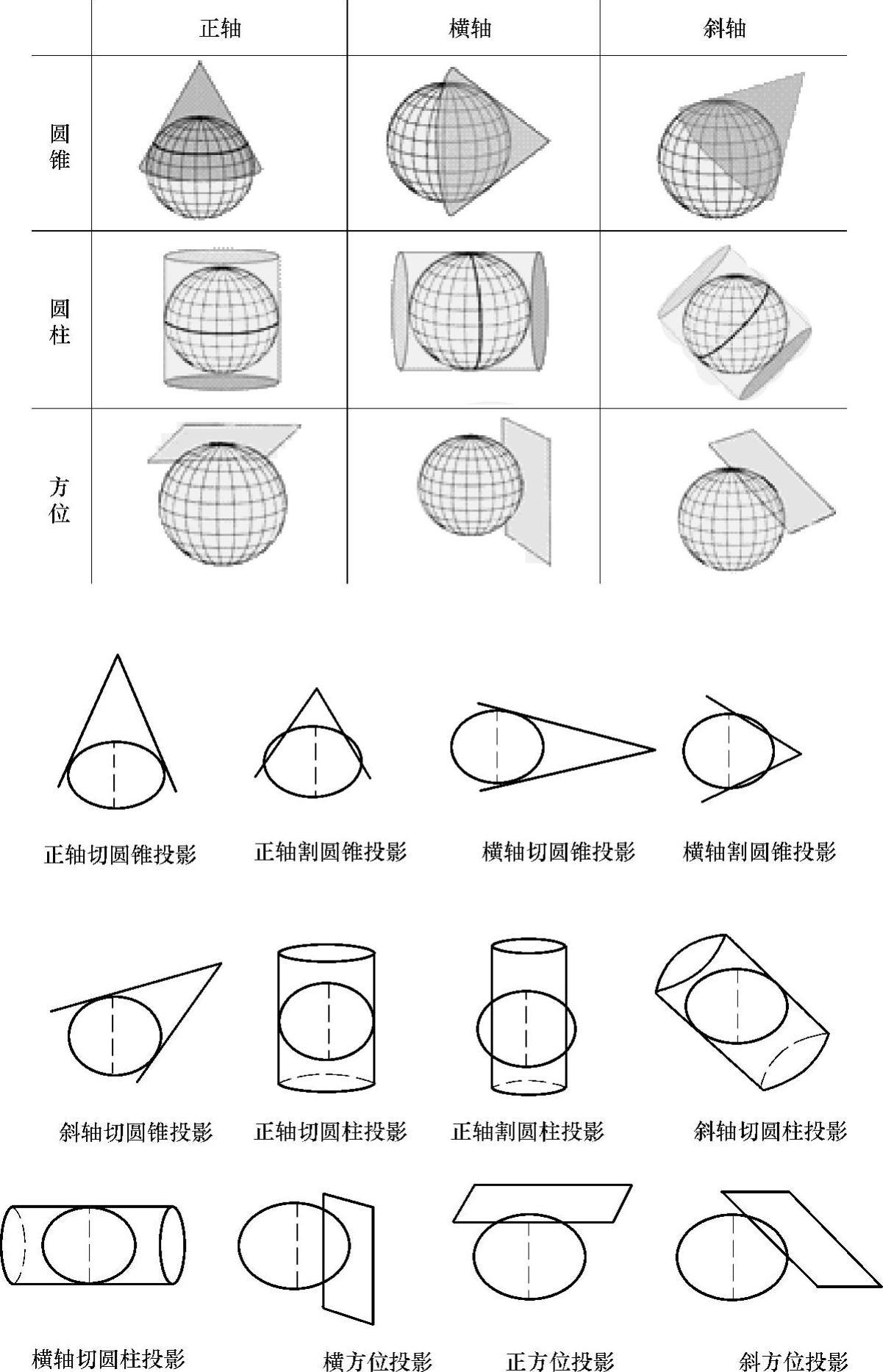
图2-5 各种投影方式示意图

我国基本比例尺地形图（1∶100万、1∶50万、1∶25万、1∶10万、1∶5万、1∶2.5万、1∶1万、1∶5000）除1∶100万以外均采用高斯-克吕格（Gauss-Kruger）投影[横轴等角切圆柱投影，又叫横轴墨卡托（Transverse Mer-cator）投影]为地理基础。1∶100万地形图采用兰伯特（Lambert）投影（正轴等角割圆锥投影），其分幅原则与国际地理学会规定的全球统一使用的国际百万分之一地图投影保持一致。海上小于50万的地形图多用墨卡托（Mercator）投影（正轴等角圆柱投影）。下面介绍几种我国海洋调查中常用的几种投影方式及其特点。

（1）高斯投影

高斯投影是目前海缆路由勘察中使用最普遍的投影方式。高斯投影是高斯-克吕格（Gauss-Kruger）投影的简称，由高斯于19世纪20年代拟定，后经克吕格于1912年对投影公式加以补充，故称为高斯-克吕格投影，是地球椭球面和平面间正形投影的一种。高斯-克吕格投影是一种等角横轴切椭圆柱投影，它是假设一个椭圆柱面与地球椭球体面横切于某一条经线上，按照等角条件将中央经线东、西各3°或1.5°经线范围内的经纬线投影到椭圆柱面上，然后将椭圆柱面展开成平面而成的，如图2-6所示。

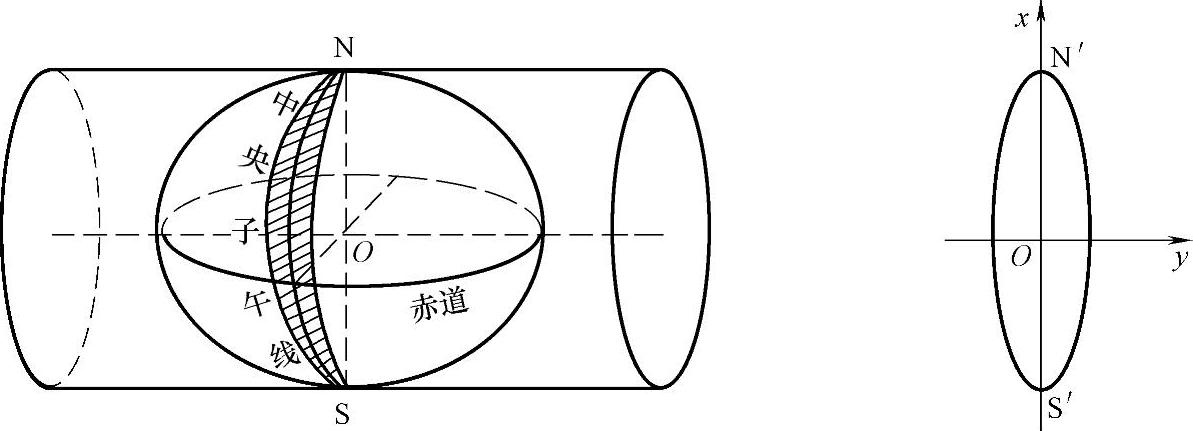
图2-6 高斯-克吕格投影方式

这种投影将中央经线投影为直线，其长度没有变形，与球面实际长度相等，其余经线为向极点收敛的弧线，距中央经线越远，变形越大。赤道线投影后是直线，但有长度变形。除赤道外的其余纬线，投影后为凸向赤道的曲线，并以赤道为对称轴，经线和纬线投影后仍然保持正交。所有长度变形的线段，其长度变形比均大于1。随远离中央经线，面积变形也愈大，为解决这一问题，采用分带投影的方法，可使投影边缘的变形不致过大。我国各种大、中比例尺地形图采用了不同的高斯-克吕格投影带。其中大于1∶1万的地形图采用3°带；1∶2.5万至1∶50万的地形图采用6°带，图2-7为高斯-克吕格投影的分带。

为了便于地形图的测量作业，在高斯-克吕格投影带内布置了平面直角坐标系统，具体方法是，规定中央经线为X轴，赤道为Y轴，中央经线与赤道交点为坐标原点，x值在北半球为正，南半球为负，y值在中央经线以东为正，中央经线以西为负。由于我国疆域均在北半球，x值均为正值，为了避免y值出现负值，规定各投影带的坐标纵轴均西移500km，中央经线上原横坐标值由0变为500km，如图2-8所示。为了方便带间点位的区分，可以在每个点位横坐标y值的百千米位数前加上所在带号。

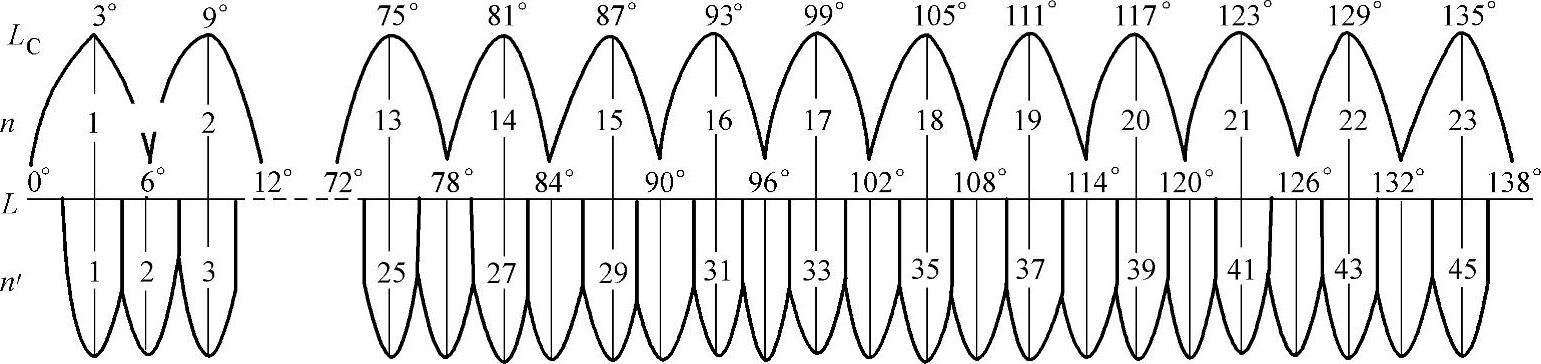
图2-7 高斯-克吕格投影的分带

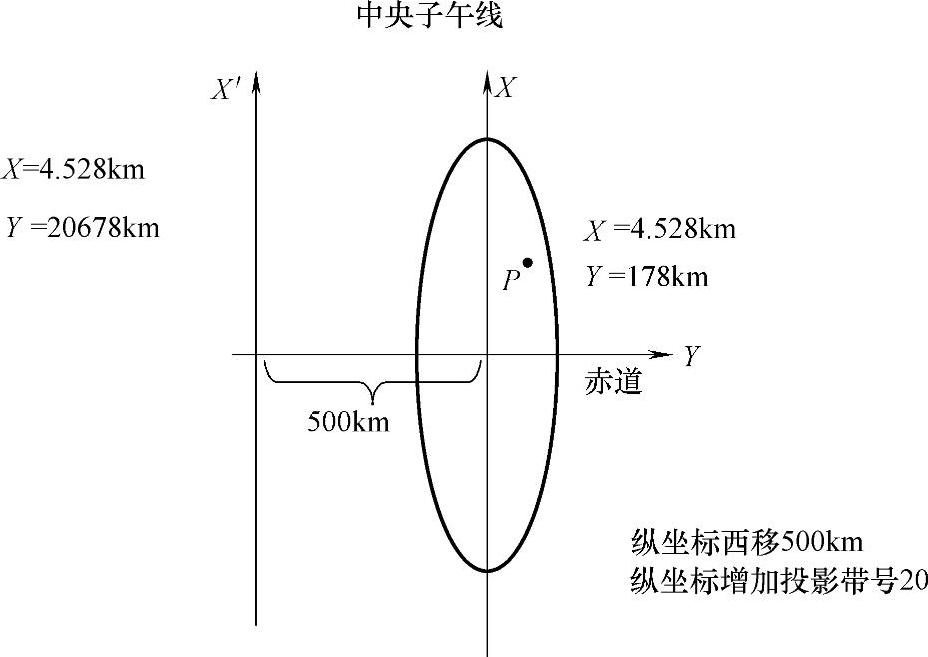
图2-8 高斯-克吕格投影坐标系的偏移

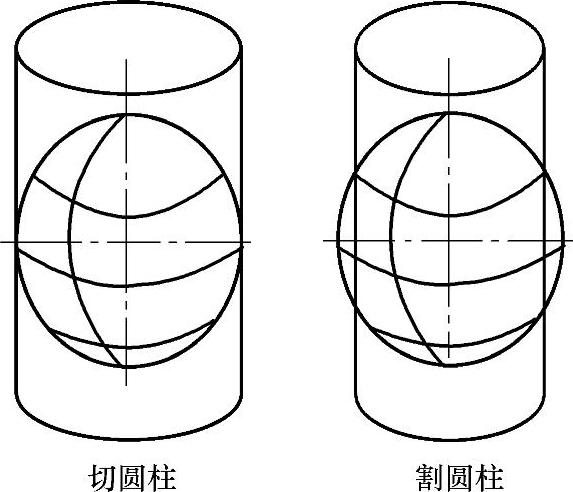
图2-9 墨卡托投影方式示意图

（2）墨卡托投影

墨卡托（Mercator）投影，是正轴等角圆柱投影，由墨卡托（G.Mercator）于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球，按等角条件，将经纬网投影到圆柱面上，将圆柱面展为平面后，即得本投影。墨卡托投影在切圆柱投影与割圆柱投影中，最早也是最常用的是切圆柱投影，又称等角圆柱投影，为地图投影方法中影响最大的，其投影方式示意如图2-9所示。

假设地球被围在一中空的圆柱里，其基准纬线与圆柱相切（赤道）接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定基准纬线上的“墨卡托投影”绘制出的地图。墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从基准纬线处向两极逐渐增大，如图2-10所示。墨卡托投影的地图上长度和面积变形明显，但基准纬线处无变形，从基准纬线处向两极变形逐渐增大，但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。在地图上保持方向和角度的正确是墨卡托投影的优点，墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。

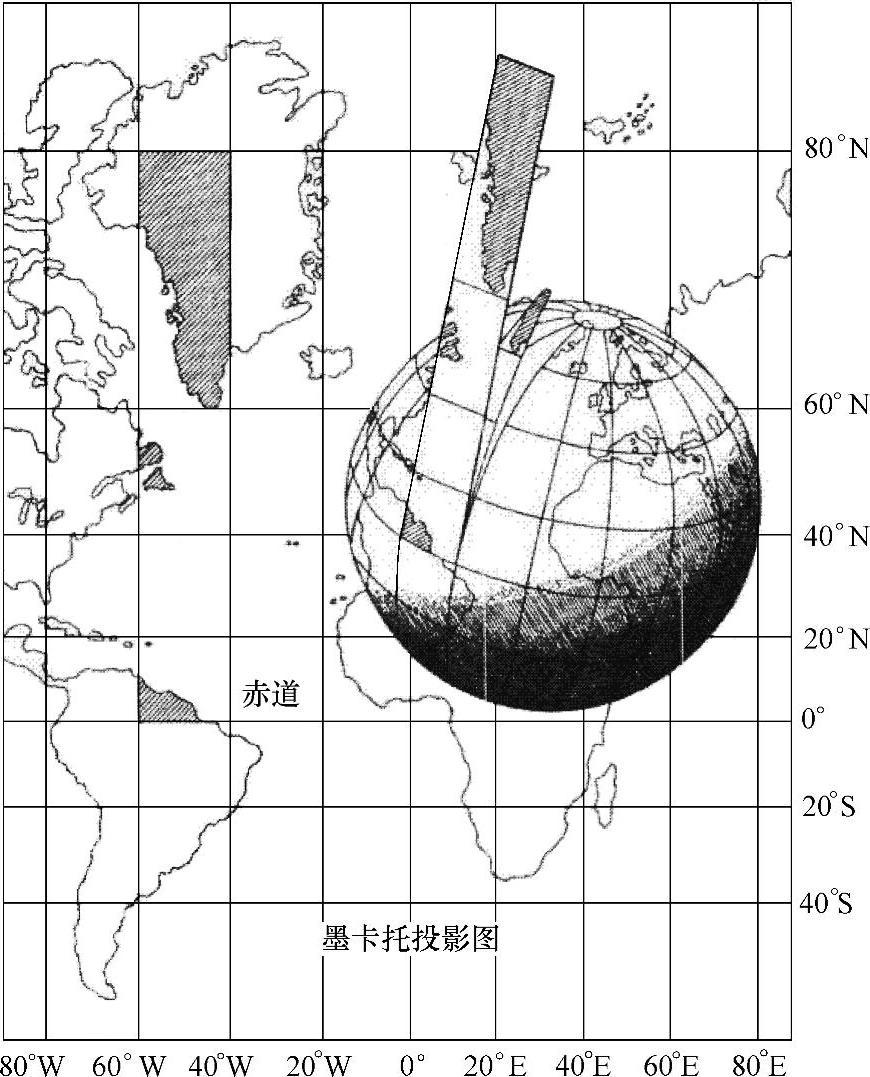
图2-10 墨卡托投影效果示意图

我国标准《海底地形图编绘规范》（GB/T 17834—1999）中5.1.3.1款规定1∶25万及更小比例尺图采用墨卡托投影，基本比例尺图（即1∶5万，1∶25万，1∶100万）采用统一基准纬线30°，非基本比例尺图以制图区域中纬为基准纬线，基准纬线取至整度或整分。