4.1.2.1 平面立体的截交线
平面立体的表面是平面图形,因此平面与平面立体的截交线为封闭的平面多边形。多边形的各个顶点是截平面与立体的棱线或底边的交点,多边形的各条边是截平面与平面立体表面的交线。
求平面立体截交线的方法:求截平面与平面立体上被截各棱的交点或截平面与立体表面的交线,然后依次连接各点所得。
例1 如图4-4(a)所示,求作正垂面P斜切正四棱锥的截交线。
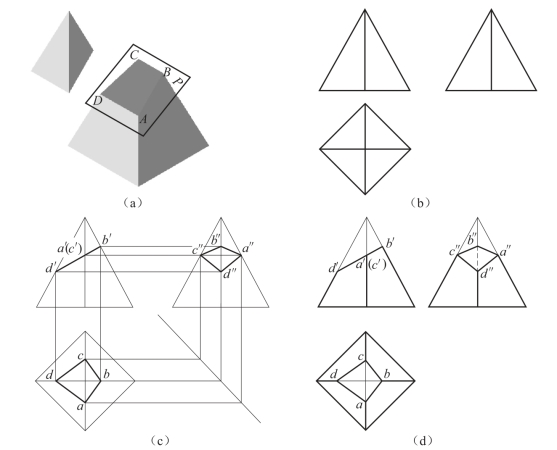
图4-4 正四棱锥截交线作图步骤
分析:截平面与棱锥的四条棱线相交,可判定截交线为四边形,其四个顶点是截平面分别与四条棱线的交点。因此,只要求出截交线的四个顶点在各投影面上的投影,然后依次连接顶点的同面投影,即得截交线的投影。
作图:
(1)绘制未切割正四棱锥的三视图,如图4-4(b)所示;
(2)首先绘制截平面的主视图,因为P为正垂面,其主视图积聚成斜线,与四棱锥四条棱线分别相交于A、B、C、D点,在主视图上表示出来后,利用直线上点的作图方法,在相应视图上求得交点的各面投影,将各面投影点依次相连,得截交线投影,如图4-4(c)所示;
(3)整理轮廓线判别可见性并加粗,如图4-4(d)所示。注意:左视图不可见棱线的投影。
例2 如图4-5(a)所示,正三棱锥带切口,已知它的正面投影,求其另两面投影。
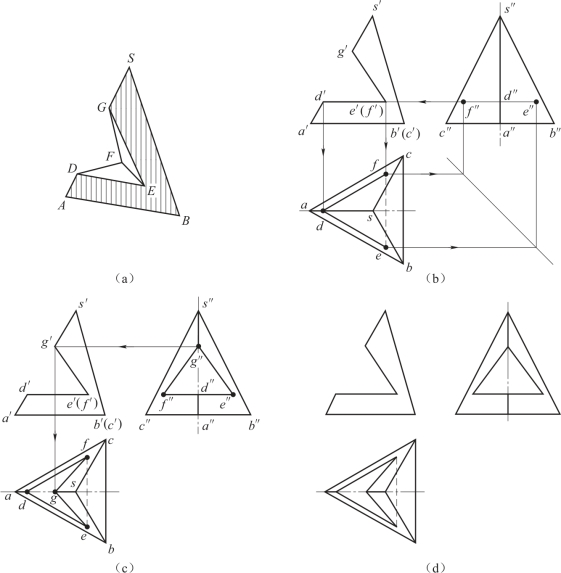
图4-5 正三棱锥截交线作图步骤
分析:该正三棱锥的切口是由两个相交的截平面切割而形成。两个截平面一个是水平面,一个是正垂面,它们都垂直于正面,因此切口的正面投影具有积聚性。水平截面与三棱锥的底面平行,因此它与棱面△SAB和△SAC的交线DE、DF必分别平行于底边AB和AC,水平截面的侧面投影积聚成一条直线,正垂截面分别与棱面△SAB和△SAC交于直线GE、GF。由于两个截平面都垂直于正面,所以两截平面的交线一定是正垂线,作出以上交线的投影即可得出所求投影。
4.1.2.2 曲面立体的截交线
根据截交线的共有性,求曲面立体的截交线,就是求截平面与曲面立体表面的共有点的投影,然后把各点的同名投影依次光滑连接起来;当截平面或曲面立体的表面垂直于某一投影面时,则截交线在该投影面上的投影具有积聚性,可直接利用面上取点的方法作图。
本节以圆柱为主要载体,介绍曲面立体截交线的画法,如图4-6所示。
根据截平面与圆柱轴线的相对位置不同,圆柱的截交线有三种不同的形状,即:
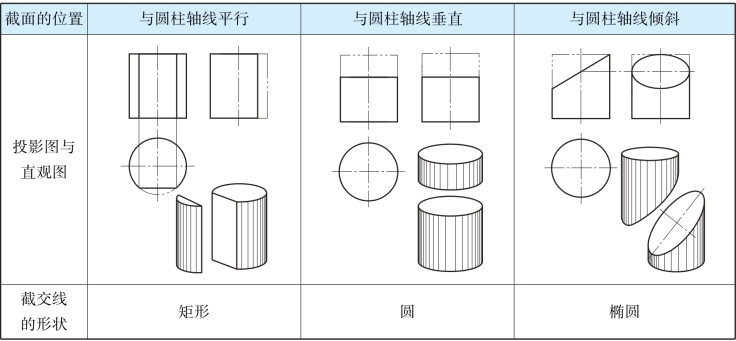
(1)截平面与圆柱轴线平行时,截交线为矩形;
(2)截平面与圆柱轴线垂直时,截交线为圆;
(3)截平面与圆柱轴线倾斜时,截交线为椭圆。
上述三种情况时的截交线见表4-1。
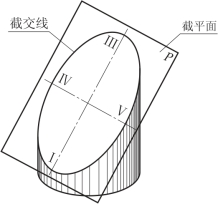
图4-6 曲面立体截交线
表4-1 圆柱截交线
例3 分析圆柱体的截交线,完成其三视图(见图4-7)。(https://www.xing528.com)
分析:截平面与圆柱的轴线倾斜,故截交线为椭圆。此椭圆的正面投影积聚为一直线。由于圆柱面的水平投影积聚为圆,而椭圆位于圆柱面上,故椭圆的水平投影与圆柱面水平投影重合,椭圆的侧面投影是它的类似形,仍为椭圆,可根据投影规律由正面投影和水平投影求出侧面投影。
作图:
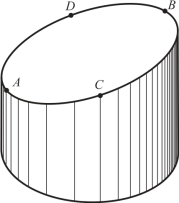
图4-7 圆柱体截交线
(1)求特殊点(特殊位置素线上的共有点)由图4-7可知,最低点A、最高点B是椭圆长轴的两端点,也是位于圆柱最左、最右转向素线上的点,最前点C、最后点D是椭圆短轴两端点,也是位于圆柱最前、最后转向素线上的点。A、B、C、D的正面投影和水平投影可利用积聚性直接作出,然后由正面投影a′、b′、c′、d′和水平投影a、b、c、d作出侧面投影,a″、b″、c″、d″,如图4-8(a)所示;
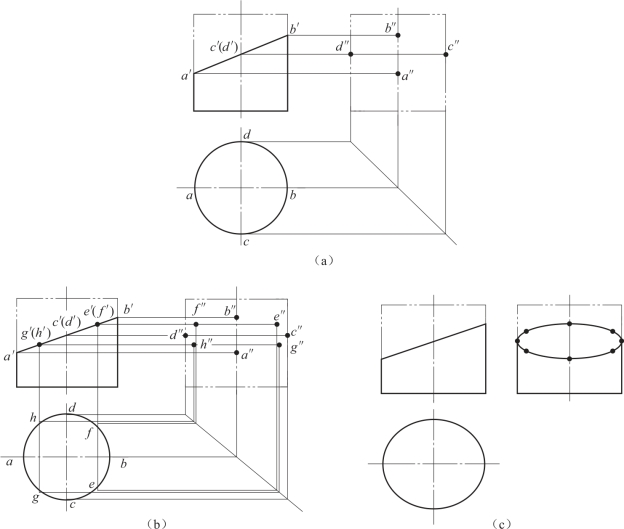
图4-8 圆柱体截交线三视图作图步骤
(2)求一般点 为了准确作图,还必须在特殊点之间作出适当数量的中间点,如E、F、G、H各点。可先作出它们的水平投影e、f、g、h和正面投影e′、f′、g′、h′,再作出侧面投影e″、f″、g″、h″如图4-8(b)所示;
(3)依次光滑连接a″、e″、c″、g″、b″、h″、d″、f″、a″,即为所求截交线椭圆的侧面投影并描深。补齐圆柱体其余轮廓线如图4-8(c)所示。
例4 求作切口圆柱体的侧面投影(见图4-9(a))。
分析:圆柱切口由水平面P和侧平面Q切割而成。如图4-9(a)所示,由于截平面P与圆柱轴线垂直,所以产生的交线应该是圆,但由于截平面P未能将圆柱体一分为二,故截交线是一段圆弧,其正面投影是一段水平线(积聚在p′上),水平投影是一段圆弧(积聚在圆柱的水平投影上);截平面P与Q的交线是一条正垂线BD,其正面投影b′d′,积聚成点,水平投影bd重合于侧平面Q的积聚投影q上。由截平面Q所产生的交线是两段铅垂线AB和CD(圆柱面上两段素线)。它们的正面投影a′b′与c′d′,积聚在q′上,水平投影分别为圆周上两个点a与b、c与d。Q面与圆柱顶面的交线是一条正垂线AC,其正面投影a′c′,积聚成点,水平投影ac与bd重合,也积聚在q上。
作图:
(1)由p′向右引投影连线,再从俯视图上量取宽度定出b″、d″(图4-9(b));
(2)由b″、d″分别向上作竖线与顶面交于a″、c″,即得由截平面Q所产生的截交线AB、CD的侧面投影a″b″、c″d″,如图4-9(c)所示;
(3)作图结果如图4-9(d)所示。
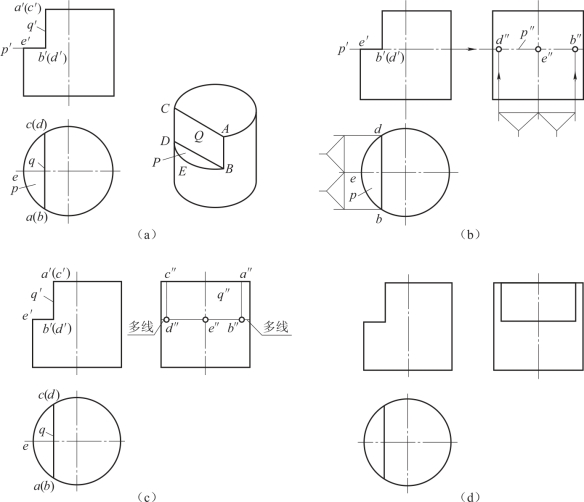
图4-9 求作带切口圆柱的侧面投影绘图步骤
例5 圆柱开槽的三视图画法(见图4-10)
分析:圆柱体被两个侧平面和一个水平面切割出直槽,两个侧平面与圆柱截交线为矩形,水平面与圆柱的截交线为圆弧。
作图(步骤见图4-11):
(1)先画出完整圆柱的三视图;
(2)画出槽的正面和水平投影。主视图中,槽的两侧面和底面分别为侧平面和水平面,其投影都积聚成直线,俯视图中,槽的两侧面仍然积聚为两直线,底面投影反映实形,两段圆弧重合在圆周上,底面与两侧面的交线分别重合在两侧面的积聚投影上;
(3)画槽的侧面投影,一个截平面一个截平面地绘制,两侧面的侧面投影反映实形——矩形,底面投影积聚为直线;
(4)整理判断可见性并描深。左视图中,圆柱体的最前和最后素线由于开槽使得C点和D点以上的部分不可见,侧面和底面交线CD段不可见。

图4-10 圆柱的开槽
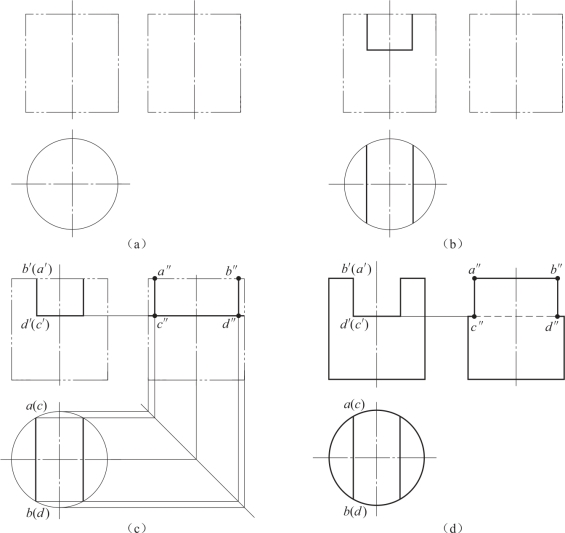
图4-11 圆柱开槽三视图绘制步骤
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




