三视图对应关系简介

3.3.2.1　三视图的位置关系

以主视图为准，俯视图在它的正下方，左视图在它的正右方，按此位置配置的三视图，不需注写其名称。

3.3.2.2　三视图的投影关系（“三等”关系）

从三视图的形成过程中，可以看出（图3-29）：

主视图反映物体的长度（X）和高度（Z）；

俯视图反映物体的长度（X）和宽度（Y）；

左视图反映物体的高度（Z）和宽度（Y）。

图3-29　三视图的“三等”关系

由此可归纳得出：

主、俯视图——长对正；

主、左视图——高平齐；

俯、左视图——宽相等。

注意：应当指出，无论是整个物体或物体的局部，其三面投影都必须符合“长对正、高平齐、宽相等”的“三等”规律，如图3-30所示。

图3-30　三视图的总体和局部“三等”关系

3.3.2.3　视图与物体的方位关系

所谓方位关系，指的是以绘图

（或看图）者面对正面（即主视图的投射方向）观察物体为准，看物体的上、下、左、右、前、后六个方位，如图3-31（a）所示；在三视图中的对应关系，如图3-31（b）所示。

主视图——反映物体的上、下和左、右；

俯视图——反映物体的左、右和前、后；

左视图——反映物体的上、下和前、后；

注意：俯、左视图靠近主视图的一边（里边），均表示物体的后面，远离主视图的一边（外边），均表示物体的前面。

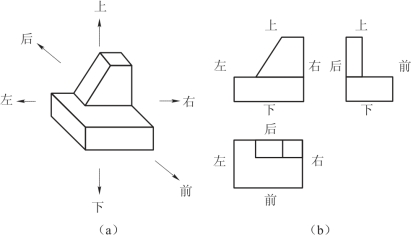
图3-31　三视图的方位关系

1.属于平面的直线和点

1）属于平面的直线

直线从属于平面的条件是：

（1）一直线经过属于平面的两点；

（2）一直线经过属于平面的一点，且平行于属于该平面的另一直线。

例3　已知平面△ABC，试作出属于该平面的任一直线，如图3-32所示。

图3-32　属于平面的直线

作法1　根据“一直线经过属于该平面的两点”的条件作图，如图3-32（a）所示。

任取属于直线AB的一点M，它的投影分别为m和m′；再取属于直线AC的一点N，它的投影分别为n和n′；连接两点的同面投影。由于M、N皆属于平面，所以mn和m′n′所表示的直线MN必属于△ABC平面。

作法2　根据“一直线经过属于该平面的一点，且平行于属于该平面的另一直线”的条件作图，如图3-32（b）所示。

经过属于平面的任一点C（c，c′），作直线CD（cd，c′d′）平行于已知直线AB（ab，a′b′），则直线CD必属平面△ABC。

2）取属于平面的点

点从属于平面的条件是：若点属于一直线，直线属于一平面，则该点必属于该平面。

因此，在取属于平面的点时，首先应取属于平面的线，再取属于该线的点。

如图3-32（a）所示，在属于△ABC平面的直线MN上取一点K的作图法。由于MN∈△ABC，又因K∈MN，所以根据点属于直线的特性可知，k′∈m′n′，如图3-32（a）所示，再过k′作OX轴的垂线，交mn于k，则k和k′即为平面△ABC内点K的两面投影。

例4　已知属于△ABC平面的点E的正面投影e′和点F的正面投影f′，试求它们的另一面投影，如图3-33（a）所示。

图3-33　属于平面的点

分析　因为点E、F属于△ABC平面，故过E、F各作一条属于△ABC平面的直线，则点E、F的两个投影必属于相应直线的同面投影。

作图，如图3-33（b）所示：①过点E作直线ⅠⅡ平行AB，即过点e′作1′2′∥a′b′，再求出水平投影12；然后过点e′作OX轴的垂线与12相交，交点即为点E的水平投影e；②过点F和定点A作直线，即过点f′作直线的正面投影f′a′，f′a′交b′c′于3′，再求出水平投影3；③然后过点f′作OX轴的垂线与a3的延长线相交，交点即为点F的水平投影f。

2.轴测图

视图是按正投影法绘制的，每个视图只能反映其二维形状，缺乏立体感。轴测图是用平行投影法绘制的单面投影图，简称轴测图。轴测图能同时反映物体长、宽、高三个方向的形状，在机械制图中常用作辅助图样。

1）轴测图的形成

将空间物体连同确定其位置的直角坐标系，沿不平行于任一坐标平面的方向，用平行投影法投射在某一选定的单一投影面上所得到的具有立体感的图形，称为轴测投影图，简称轴测图，如图3-34所示。(www.xing528.com)

图3-34　轴测图的形成

在轴测投影中，我们把选定的投影面P称为轴测投影面，把空间直角坐标轴OX、OY、OZ在轴测投影面上的投影O1X1、O1Y1、O1Z1称为轴测轴；把两轴测轴之间的夹角∠X1O1Y1、∠Y1O1Z1、∠X1O1Z1称为轴间角；轴测轴上的单位长度与空间直角坐标轴上对应单位长度的比值，称为轴向伸缩系数。OX、OY、OZ的轴向伸缩系数分别用p、q、r表示。例如，如图3-34所示，p=O1A1/OA，q=O1B1/OB，r=O1C1/OC。强调：轴间角与轴向伸缩系数是绘制轴测图的两个主要参数。

常见轴测图的轴间角和轴向伸缩系数如表3-6所示。以下介绍正等轴测图的内容，其他轴测图请读者参照表3-6自行分析。

表3-6　常见轴测图的轴间角和轴向伸缩系数

2）正等测图的形成及参数

如图3-35所示，如果使三条坐标轴OX、OY、OZ对轴测投影面处于倾角都相等的位置，把物体向轴测投影面投影，这样所得到的轴测图投影就是正等测轴测图，简称正等测图。

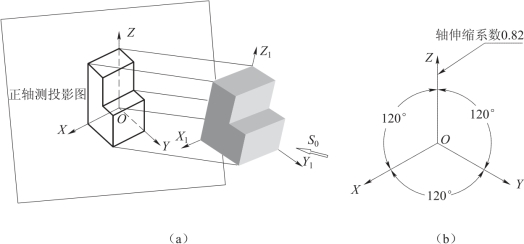
图3-35　正等测图

如图3-35（b）所示，正等测图的轴测轴、轴间角和轴向伸缩系数等参数及画法。从图中可以看出，正等测图的轴间角均为120°，且三个轴向伸缩系数相等。经推证并计算可知p1=q1=r1=0.82。为作图简便，实际画正等测图时采用p1=q1=r1=1的简化伸缩系数画图，即沿各轴向的所有尺寸都按物体的实际长度画图。但按简化伸缩系数画出的图形比实际物体放大了1/0.82≈1.22倍。

3）长方体的正等测图

分析：根据长方体的特点，选择其中一个角顶点作为空间直角坐标系原点，并以过该角顶点的三条棱线为坐标轴，先画出轴测轴，然后用各顶点的坐标分别定出长方体的八个顶点的轴测投影，依次连接各顶点即可。

作图方法与步骤如图3-36所示：

（1）先在正投影图上定出原点和坐标轴的位置。我们选定右侧后下方的顶点为原点，经过原点的三条棱线为OX、OY、OZ轴，如图3-36（a）所示；

（2）画出轴测轴O1X1、O1Y1、O1Z1，如图3-36（b）所示；

（3）在O1X1轴上量取长方体的长度a，在O1Y1轴上量取长方体的宽度b，画出长方体底面的轴测投影，如图3-36（c）所示；

（4）过底面各顶点向上作O1Z1的平行线，在各线上量取长方体的高度h，得到顶面上各点并依次连接，得长方体顶面的轴测投影如图3-36（d）所示；

（5）擦去多余的图线并描深，即得到长方体的正等测图，图3-36（e）所示。

4）正六棱柱体的正等测图

分析：由于正六棱柱前后、左右对称，为了减少不必要的作图线，从顶面开始作图比较方便，故选择顶面的中点作为空间直角坐标系原点，棱柱的中心线作为OZ轴，顶面的两条对称线作为OX、OY轴。然后用各顶点的坐标分别定出正六棱柱的各个顶点的轴测投影，依次连接各顶点即可。

图3-36　长方体的正等测图

作图方法与步骤如图3-37所示：

图3-37　正六棱柱的正等测图

（1）选定直角坐标系，以正六棱柱顶面的中点为原点（坐标系原点可以任定，但应注意对于不同位置原点，顶面和底面各顶点的坐标不同），如图3-37（a）所示；

（2）画出轴测轴O1X1、O1Y1、O1Z1；

（3）在O1X1轴上量取O1M、O1N，使O1M=Om、O2N=On，在O1Y2轴上以尺寸b来确定A、B、C、D各点，依次连接六点即得顶面正六边形的轴测投影，如图3-37（c）所示；

（4）过顶面正六边形各点向下作O1Z1的平行线，在各线上量取高度h，得到底面上各点并依次连接，得底面正六边形的轴测投影，如图2-37（d）所示；

（5）擦去多余的图线并描深，即得到的正六棱柱体正等测图，如图3-37（e）所示。

5）圆的正等测图

用“四心法”作圆的正等测图，“四心法”画椭圆就是用四段圆弧代替椭圆。下面以平行于H面（即XOY坐标面）的圆为例，如图3-38所示，说明圆的正等测图的画法。

图3-38　圆的正轴测图画法

其作图方法见本教材第2章“知识拓展　椭圆的画法”图2-25。

6）圆柱和圆台的正等测图

如图3-39所示，作图时，先分别作出其顶面和底面的椭圆，再作其公切线即可。

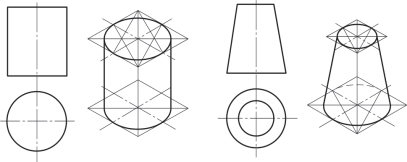
图3-39　圆柱和圆台的正等测图画法

投影分正投影和中心投影，我们平常看到物体的投影属于中心，它不能反映物体的真实尺寸，只能反映物体的轮廓。我们通常采用正投影来反映物体的形状和真实尺寸。例如正三棱锥，如图3-40（a）所示，我们通过正投影，从三个方向进行投射，生成其二维的平面图形，如图3-40（b）所示来反映其形状和尺寸。

1.建立投影法的概念，掌握正投影法的基本原理和正投影的基本性质；

2.掌握三视图的形成及“三等”规律，并能运用正投影法绘制简单立体的三视图；

图3-40　正六棱锥及其三视图

（a）正六棱锥；（b）正六棱锥三视图

3.掌握点、直线、平面在三面投影体系中的投影特性，在直线、平面上取点以及在平面上取直线的作图方法；

4.掌握几何体的投影特性，在几何体表面取点、线的作图方法。