点是最基本的几何要素,为了迅速而正确地画出物体的三视图,必须掌握点的投影规律。例如图3-4(b)所示的正三棱锥,是由△SAB、△SBC、△SCA、△ABC四个棱面所组成,各棱面分别交于棱线SA、SB、…,各棱线汇交于顶点A、B、C、S,显然,绘制三棱锥的投影图,实质上就是画出这些顶点的各面投影,然后依次连线而成,如图3-4(a)所示。
点的表示法:空间点用大写字母或罗马数字,例如A、B、C或Ⅰ、Ⅱ、Ⅲ…;水平投影用相应的小写字母或相应的阿拉伯数字,如a、b、c或1、2、3…;正面投影用相应的小写字母或相应的阿拉伯数字a′、b′、c′或1′、2′、3′…;侧面投影用相应的小写字母或相应的阿拉伯数字,如a″、b″、c″或1″、2″、3″…。
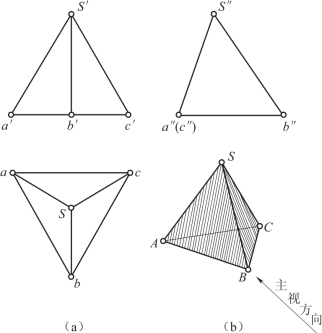
图3-4 物体上点的投影分析示例
3.1.2.1 三投影面体系的建立
三投影面体系由三个相互垂直的投影面所组成,如图3-5所示。
三个投影面分别为:
正立投影面,简称正面,用V表示;
水平投影面,简称水平面,用H表示;
侧立投影面,简称侧面,用W表示。
相互垂直的投影面之间的交线,称为投影轴,它们分别是:
OX轴(简称X轴),是V面与H面的交线,它代表长度方向;
OY轴(简称Y轴),是H面与W面的交线,它代表宽度方向;
OZ轴(简称Z轴),是V面与W面的交线,它代表高度方向。
三根投影轴相互垂直,其交点O称为原点。
为了画图方便,需将互相垂直的三个投影面摊平在同一个平面上。规定:正立投影面保持不动,将水平投影面OX轴向下旋转90°,将侧立投影面绕OZ轴向右旋转90°,分别重合到正立投影面上。应注意:水平投影面和侧立投影面旋转时,OY轴被分为两处,分别用OYH(在H面上)和OYW(在W面上)表示,如图3-6所示。

图3-5 三面投影体系

图3-6 三投影面体系的展开
3.1.2.2 点的三面投影
如图3-7所示,求点A的三面投影,就是由点A分别向三个投影面作垂线,则其垂足a、a′、a″即为点A的三面投影图。如将投影面摊平在一个平面上,便得到点A的三面投影图,如图3-7(b)所示。图中ax、ayh、ayw、az分别为点的投影连线(用细实线绘制)与投影轴X、Y、Z的交点。
通过点的三面投影图的形成过程,可总结出点的投影规律:
(1)点的两面投影的连线,必定垂直于相应的投影轴。即:
aa′⊥OX,a′a″⊥OZ,而aayh⊥OYh,a″ayw⊥OYW。
(2)点的投影到投影轴的距离,等于空间点到相应的投影面的距离,即“影轴距等于点面距”。
a′ax=a″ayw=A点到H面的距离Aa;
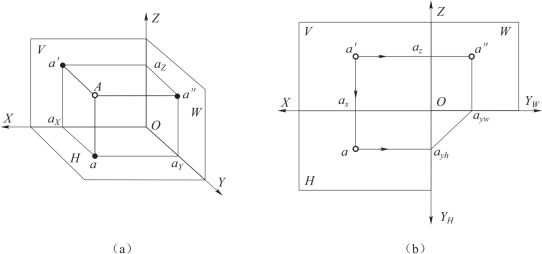
图3-7 点的三面投影
(a)点在三面投影体系中的投影;(b)展开图
aax=a″az=A点到V面的距离Aa′;
aayh=a′az=A点到W面的距离Aa″。
3.1.2.3 点的投影与直角坐标的关系
点的空间位置可用直角坐标来表示,如图3-8所示。即把投影面当作坐标面,投影轴当作坐标轴,O即为坐标原点。则:
A点的X坐标xA等于A点W面的距离Aa″;
A点的Y坐标yA等于A点到V面的距离Aa′;
A点的Z坐标zA等于A点到H面的距离Aa。
点A坐标的规定书写形式为:A(xA,yA,zA)。
例1 已知点A(20,10,30),求作它的三面投影图。
作法1(图3-9(a))
(1)作投影轴OX、OYH、OYW、OZ;(https://www.xing528.com)
(2)在OX轴上由O点向左量取20,得ax点;在OYH、OYW轴上由O点分别向下、向右量取10,得出ayh、ayw;在OZ轴上由O向上取30,得出az;
(3)过ax作OX轴的垂线,过ayh、ayw分别作OYH、OYW轴的垂线,过az作OZ轴的垂线;
(4)各条垂线的交点a、a′、a″,即为A点的三面投影。
作法2(图3-9(b))
(1)作投影轴OX、OYH、OYW、OZ;
(2)在OX轴上由O点向左量取20,得ax点;
(3)过ax作OX轴的垂线,并沿垂线向下量取10,得axa=10,向上量取30,得a′;
(4)根据a、a′,求出第三投影a″。

图3-8 点的投影与坐标的关系
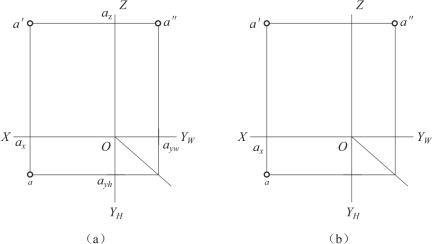
图3-9 根据点的坐标作投影图
3.1.2.4 两点的相对位置
两点在空间的相对位置,由两点的坐标差来确定,如图3-10所示。
两点的左、右相对位置由x坐标差(xA-xB)确定。由于xA>xB,因此点B在点A的右方;
两点的前、后相对位置由y坐标差(yA-yB)确定。由于yA<yB,因此点B在点A的前方;
两点的上、下相对位置由z坐标差(zA-zB)确定。由于zA>zB,因此点B在点A的下方;
故点A在点B的左、后、上方,反过来说,就是B点在A点的右、前、下方。
如图3-11所示A、B两点的投影中,a和b重合,这说明A、B两点的x、y坐标相同,xA=xB、yA=yB,即A、B两点处于对水平面的同一条投射线上。
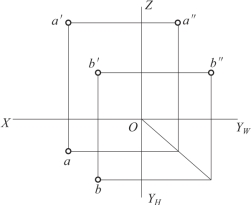
图3-10 两点相对位置

图3-11 重影点的可见性判断
可见,共处于同一条投射线上的两点,必在相应的投影面上具有重合的投影,这两个点被称为对该投影面的一对重影点。
重影点的可见性需根据这两点不重影的投影的坐标大小来判别。即:
当两点在V面的投影重合时,需判别其H面或W面投影,则点在前(y坐标大)者可见;
当两点在H面的投影重合时,需判别其V面或W面投影,则点在上(z坐标大)者可见;
若两点在W面的投影重合时,需判别其H面或V面投影,则点在左(x坐标大)者可见;
如图3-11所示中,a、b重合,但正面投影不重合,且a在上b在下,即zA>yB。所以对H面来说,A可见,B不可见。在投影图中,对不可见的点,需加圆括号表示。如图3-11所示中,对不可见点B的H面投影,加圆括号表示为(b)。
例2 在已知点A(20,20,10)的三面投影图上(图3-12),作点B(30,10,0)的三面投影,并判断两点在空间的相对位置。
分析:点B的z坐标等于0,说明点B属于H面上,点B的正面投影b′一定在OX轴上,侧面投影b″一定在OYW轴上。
作图:在OX轴上由O点向左量取30,得bx(b′重合于该点),由bx向下作垂线并取bxb=10,得b。根据作出的b、b′,即可求得第三投影b″,如图3-13所示。应注意,b″一定在W面的OYW轴上,而绝不在H面的OYH轴上。

图3-12 点A的三面投影
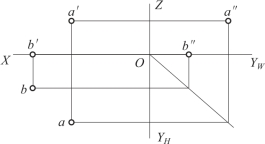
图3-13 点A、B两点的三面投影
判别A、B两点在空间的相对位置:
左、右相对位置:xB-xA=10,故点A在点B右方10 mm。
上、下相对位置:zA-zB=10,故点A在点B上方10 mm;
前、后相对位置:yA-yB=10,故点A在点B前方10 mm;
即点A在点B的右、前、上方各10 mm处。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




