采用二维DDA对如图13-26所示的支墩坝坝基稳定性进行计算，共进行400时步。时间间隔由程序自动选择，控制最大位移比率0.001。最大位移比率定义是允许的最大步长位移与整个模型高度1/2的比值。各时步的平均时间间隔为0.06s，动力系数为0.0，即下一个时步的速度为0。
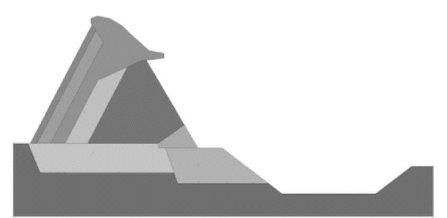
图13-26 承受水压力的支墩坝
图13-26例中大坝的物理力学参数表如表13-10所示。该算例经过200时步的计算后，其最大相对位移达到0.0000000，表明此时块体系统以很高的精度达到极限平衡状态。
图13-27为采用二维DDA对计算支墩坝的破坏模式。计算时总的时步为5000，控制最大位移比率0.001，时间间隔由程序自动选择。最大位移比定义是允许的最大时步位移与整个网格高度1/2的比值。每时步的平均时间为0.8s，动力系数为0.0，这表明下一个时步的速度为0。图13-27例中大坝的物理力学参数如表13-10所示。为使大坝破坏，水平节理的摩擦角从28°降至17°。
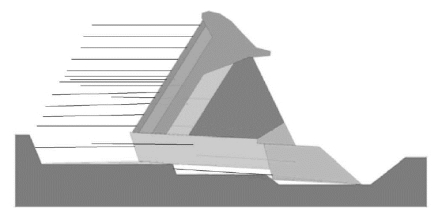
图13-27 承受水压力与降低摩擦角时支墩坝的破坏模式
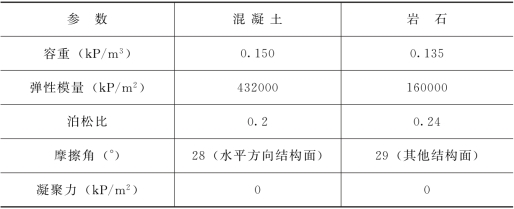
表13-10 混凝土与拱基岩体的力学参数
(www.xing528.com)
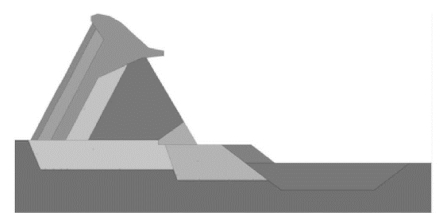
图13-28 有抗力体与水荷载作用的支墩坝
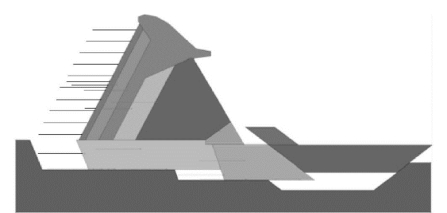
图13-29 上游承受水荷载且摩擦角较小时的支墩坝的破坏模式
采用二维DDA法对于图13-27例中的坝基稳定进行分析计算，总的时步为5000，最大位移比0.0007，时间间隔由程序自动选择和控制。最大位移比是允许的最大步位移与模型高度1/2的比值。各时步的平均时间间隔为0.08s，动力系数为0.0，即下一个时步的速度为0。该算例的物理力学参数如表13-10所示。计算时为使大坝达到破坏状态，将水平方向结构面的摩擦角从28°降低至17°。
采用二维DDA法对图13-28例中坝基加固后的破坏模式进行分析，计算进行了500时步，最大位移比0.007，时间间隔根据最大位移比自动选择和控制。最大位移比定义为允许的最大步位移与整个模型高度1/2的比值。各步的平均时间间隔为0.044s，动力系数为0.0，即下一个时步的速度为0。
图13-28例中水平方向节理与其他节理的摩擦角分别为17°与45°，其他参数如表13-10所示。本算例经过200时步的迭代后相对最大位移为0.0000000，表明此时块体系统以高精度达到极限状态。
采用二维DDA法对图13-29例加固坝基的破坏模式进行计算，共进行5000次时步的迭代。时间间隔由最大位移率0.001自动选择和控制。最大位移率定义为最大步位移与整个模型高度1/2的比值。每时步的平均时间间隔为0.06s，动力系数为0.0，即下一个时步的速度为0。
图13-29例中水平方向结构面与其他方向结构面的摩擦角分别为17°与0°，其他物理力学如表13-10所示，非水平方向的结构面导致坝基被破坏。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
