倾倒边坡锚固计算优化方式

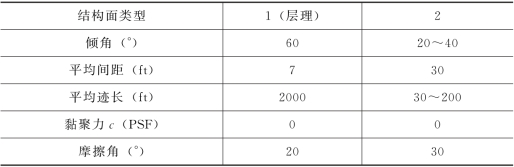
本节讨论三种工况的边坡锚固计算。在这三种工况中，边坡中发育的第一组结构面均为倾角为60°的层面，工况一中第二组结构面为长大的节理，工况二与工况三中第二组结构面为短而小的节理，但工况三中节理面倾角较缓，为20°。计算中考虑地下水的作用。表13-4为结构面的几何与力学参数。

表13-4　结构面的几何与力学参数

采用二维DDA法共执行3000时步的计算，每时步为0.002s，动力系数为1.00，即下一个时步的速度保持前一时步的速度。在动力计算中可以考虑地震力的影响。图13-9为层面倾角为60°时边坡锚固的计算结果。

图13-9　层面倾角为60°时倾倒边坡的锚固计算结果(www.xing528.com)

图13-10　层面倾角为60°时的锚固力随时间的变化关系

图13-10为图13-9例中锚固力随时间的变化关系曲线。从计算结果可以看出，不同工况条件下的锚固力的差异十分明显。当层面的倾角为60°时，整个边坡剖面所需要的最大锚固力为14 kips/ft。因此，对不同类型的边坡采用不同的加固方法更为合理。

由于层面分布密集、岩层很薄，因此有大量的块体需要计算。由于目前没有以往的经验来处理这种倾倒破坏的边坡，本例中包括了所有可能的组合。

计算中考虑了运动的时间效应。每次计算必须由动态状态到达静态状态。由于时间足够长，计算结果没有发现较大的位移或锚固力的变化。