Goodman和Bray(1976)提出的边坡倾倒稳定分析方法是将滑坡体用反倾向的结构面切割成n块宽度为ΔL的矩形条块,对于任一条块,作用其上的力将使该条块处于:①稳定;②倾倒破坏;③滑动三种破坏状态。滑坡体分为稳定区、倾倒区、滑动区三部分,如图9-1所示。
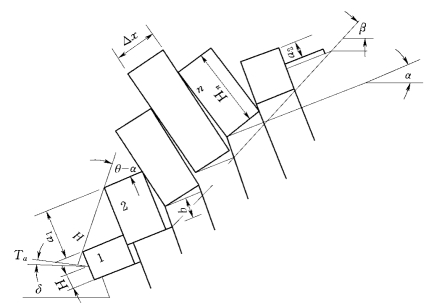
图9-1 边坡的典型结构特征
已知条块右侧作用力的合力,可以根据力的平衡求得左侧合力。对倾倒块体,将各作用力对条块左下端点取矩

图9-2为Hoek和Bray(1977)提供的一个算例。开挖边坡高92.5m,坡角为56.6°,岩体倾角60°,为倾向山体的层状岩体。将破坏岩体分为16个岩块,γ=25k N/m3。条柱底面和侧面的摩擦角φ均为38.15°。编号10的岩块处于边坡的坡顶线上,坡顶面仰角为4°。由于cotα=1.78,摩擦角φ>30°(tanφ=0.577),岩块16、15及14构成一稳定区。
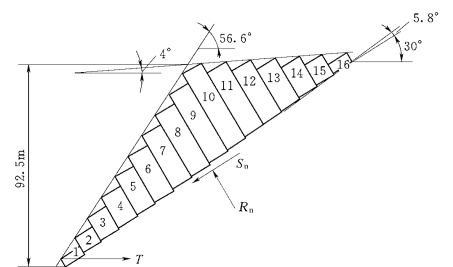
图9-2 Hoek和Bray(1977)提供的一个算例
取tanφ=0.7855,P13=0,P12按式(9-1)和式(9-2)计算的P12的较大者。从岩块16到岩块4以前倾倒力的数值都比较大,而从岩块3以后滑动力的数值比较大。所以,岩块4至13构成潜在的倾倒区,而岩块1至3构成了滑动区。阻止岩块1滑动所需要的抗滑力趋于零,说明该边坡非常接近极限平衡状态。
很显然,这是一个精心设计的恰好处于极限平衡状态的边坡,在一般情况下,在坡脚处需要施加一个外力Ta,当Ta>0时,边坡处于不稳定状态,反之,则处于稳定状态。
将Goodman和Bray的经典倾倒算例用DDA方法进行计算,将计算结果与之进行对比。设条柱底面和侧面的摩擦角φ均为38.149°(tanφ=0.7855)。在计算的过程中,首先是下部的1~3块产生滑动,其后的4~13号岩柱绕底部产生旋转,由于岩块底部旋转时是角对角接触,不容易保持平衡,同时由于底接触面台阶限制了岩柱的旋转空间,岩柱在旋转的同时,向下有错动。在变形的过程中,岩柱间由于转动角度有差别而张开,产生裂缝,块体间面与面接触变为点与面接触,如图9-3所示。(https://www.xing528.com)

图9-3 中间结果,点对面接触示意图
图9-4是迭代计算结束后位移彩色渲染图,随着1~3号块体向下滑动,4~13号岩柱有更大的逆时针旋转的空间,岩柱间重新恢复到面与面接触,倾倒变形停止,边坡重新回到稳定状态。从图中可以看到,最大位移发生在10号岩柱的顶部,位移矢量为15.53m。
为了分析倾倒位移的产生,发展和收敛过程,在10号块体顶端设置一个测点,在迭代过程中记录测点的水平位移,垂直位移和位移矢量。图9-5位移过程线中,测点位移开始比较缓慢,然后加速,最后趋缓并最终达到平衡状态。
从DDA计算倾倒变形的过程中可以看到,1~3号块体向下滑动,4~13号岩柱倾倒旋转,14~16号岩柱是稳定的,与理论解完全一致。

图9-4 摩擦角φ=38.149°,倾倒变形结束后位移图
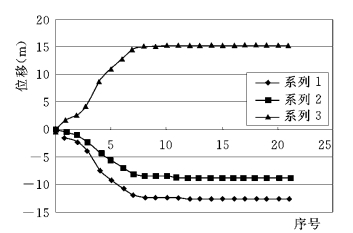
图9-5 10号岩柱顶端测点位移过程线
系列1—水平位移;系列2—垂直位移;系列3—位移矢量
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




