基于数值模拟的非连续变形分析方法优化

用非连续变形分析方法对离心机试验结果进行数值模拟。数值方法模拟离心机试验成果有两种方法:一种方法是重力场模拟，数值模型与试验模型尺寸相等，重力采用模型破坏时的重力加速度值，例如当离心机加速度为78g时，试验模型发生破坏，此时计算模型的垂直方向重力应取为石膏的重力值的78倍；另一种方法是尺寸效应模拟，将试验模型尺寸放大78倍，实现等效应的试验重力场。本次石膏材质倾倒试验非连续变形分析数值模拟采用等效应力场方法。

数值模型破坏后如图8-5所示，在迭代过程中，在上部块体的挤压下，最下部块体最先出现滑动；其上第2～第8块先后接连发生倾倒。稍向下错动后，绕基座台阶产生角对角转动，推动滑动块继续向下滑动。当滑动块与倾倒块之间产生一定的空间后，第2块(倾倒块)底滑面在底座台阶的角上产生滑动，由角对角转动变换成角对边的滑动；当倾倒块右下角接触到下一台阶后，又转换为倾倒块右下角对下一台阶边的转动。而上部的倾倒块体仍是绕基座台阶产生角对角转动。首先是第2块产生角对边滑动，当第2块与第3块之间有足够空间后，然后是第3块产生角对边滑动；依次逐块向上发展。当块体与块体界面之间由角对边转换成为边对边后，倾倒石膏块恢复连续的面与面接触，倾倒变形结束。数值模拟的块体倾倒过程与离心倾倒模型试验的倾倒破坏的录像非常相似。

图8-5　数值模型破坏后的变形状态

图8-5是数学模型破坏后重新回到稳态时的图像。块体倾角产生翻转，边坡的形态发生变化，阻止块体进一步翻转所需的摩擦角进一步增大，倾倒块体恢复连续的面与面接触，最后回到平衡状态，倾倒变形结束。

图8-6表示迭代过程与倾倒块体安全系数收敛曲线，最后的安全系数趋于一个稳定值，达到稳态。(https://www.xing528.com)

通过对比非连续变形分析数值模拟与离心机试验倾倒破坏过程及最终结果可以看到:滑动块、倾倒块和稳定块的分布与模型试验完全相同；倾倒过程中块体的运动形态基本一致；当块与块界面之间由角对边转换成为边对边后，倾倒石膏块恢复连续的面与面接触，倾倒变形结束。

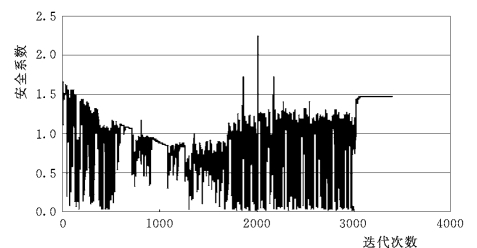
图8-6　安全系数收敛曲线

数值模拟与离心机试验倾倒破坏最终结果基本吻合，对比模型边坡破坏后的照片和数值模拟的结果，第9块的位移状态有些差别，因为试验模型箱的空间不够，最下面滑动块最后抵住了模型箱的侧壁，位移不够充分的缘故。

在倾倒变形过程中，第10块、第11块始终属于稳定块，符合Goodman倾倒数学模型中关于将倾倒变形分为滑动区、倾倒区和稳定区的理论，与离心倾倒模型试验和理论解完全吻合。