求平面的赤平投影的介绍，

已知平面，其倾向β，倾角为α，为其作赤平投影。

通过参照球面中心平面的赤平投影为大圆，故要作平面的赤平投影，首先要确定该投影圆的圆心位置和半径。

沿倾向方向作参照球面的竖向剖面如图6-2(a)所示，图中POP′为该平面的交线，而OP′为其倾向的矢量。OP的赤平投影为点P′，因此，图中直线PP′则为所求大圆的直径，其等分点C即为圆心。由图6-2中各角度关系，可求出大圆的圆心和半径θ=45—α/2，CF=P′C=CP=r。

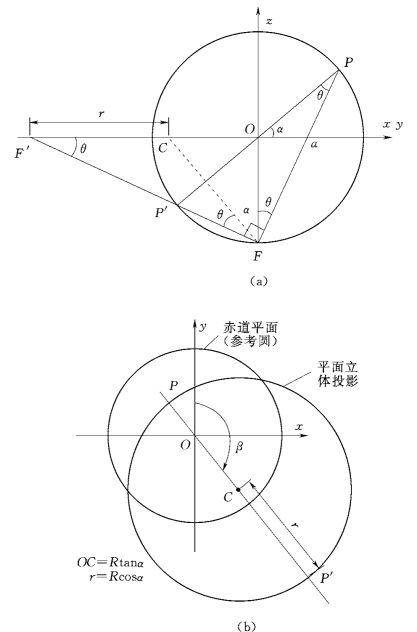
图6-2　平面的赤平投影

(a)竖向剖面图；(b)赤平投影

(www.xing528.com)

该平面投影大圆的圆心坐标为

YCW方法也是采用赤平投影图来判断失稳模式，不过与块体理论的赤平投影方法略有不同。块体理论是画结构面的赤平投影大圆。而YCW方法是画结构面法向矢量的赤平投影点，采用等面积投影法(或称Wuff法，吴氏法，如图6-3所示)。采用下半球投影时，以南极为圆心，以其与极点A连线为半径作铅直圆弧，交于与南极相切的水平面于B′点，同样，B′点也唯一规定了一个结构面的产状。为了使球面上一个圆上的所有点投影到水平面后形成的圆的直径不变，吴氏法规定B′点要在径向缩短到达新的B点。

等面积投影的优点是矢量投影到赤道平面上时，其相对位置不会发生变态，能够准确的统计在为在赤道平面上投影极点的密度。

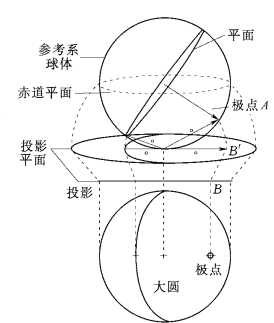
图6-3　等面积投影