法向弹簧子矩阵的计算方法

设P1是顶点，P2P3是进入线，(xk，yk)和(uk，vk)分别是Pk(k=1，2，3)的坐标和位移。如点P1，P2和P3从ox向oy同一方向转动，见图3-7，则从P1到线P2P3的距离d为

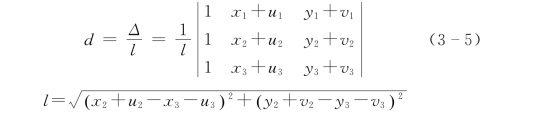
如P1越过边P2P3，则d应当是负值。

步位移

因时步很小故是小值。根据接触的定义，接触距离Δ/l是小值。

令

忽略二阶无限小，有

公式l可简化为

考虑只有一阶小

设P1点属于第i块而边P2P3属于第j块，点P1、P2和P3的位移可表示为

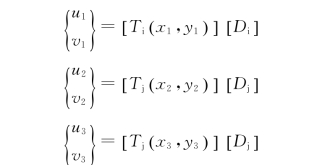
根据式(3-5)，d可表示为

式中

表示弹簧刚度为p及相互嵌入距离为d，接触弹簧的应变能为

(www.xing528.com)

式中，p是一个很大的正数。p值通常是10～100E，以保证弹簧位移小于块体的10—1～10—3倍。如p足够大，计算结果将与p的选择无关。

对∏k取导使极小化，可得四个6×6子矩阵和两个6×1子矩阵，并分别加到[Kii]、[Kij]、[Kji]、[Kjj]、[Fi]和[Fj]中。

∏k的微商

形成6×6子矩阵，将其加到总体方程(2-5)的子矩阵[Kii]中。

∏k的微商

形成6×6子矩阵，它被加到总体方程(2-5)的子矩阵[Kij]中。

∏k的微商

形成6×6子矩阵，它被加到总体方程(2-5)的子矩阵[Kji]中。

∏k的微商

形成6×6子矩阵，它被加到总体方程(2-5)的子矩阵[Kji]中。

∏k的微商

最后形成6×6子矩阵，将子矩阵加到总体方程(2-5)的子矩阵[Fi]中。

∏k的微商

最后形成6×6子矩阵，将其加到总体方程(2-5)的子矩阵[Fj]中。