【摘要】:两个块体在下一步相碰的可能性只考虑它们在当前步是否靠近,可以按通常数学方法测定它们之间的距离。根据式(3-1)的距离定义,只有当ηij=0时块i与块j是接触或重叠的,否则ηij>0。由式(3-1)很明显,如果距离η大于所有块体点的距离ρ的两倍,即ηij>2ρ,则对块体i和块体j在下一步时间内不可能相碰。定义距离的式(3-1)可写成对计算更有效的形式式中,Bi及Bj分别是块体i与块体j的边界段;Vi及Vj分别是块体i与j的顶点。
非连续变形分析可以计算大位移和大变形,块体位置、块体形状和块体接触随荷载步或时步变化。在每一迭代步结束后,必须判断在下一步中所有可能接触的成对块体。两个块体在下一步相碰的可能性只考虑它们在当前步是否靠近,可以按通常数学方法测定它们之间的距离。
块体i与块体j间的距离规定为任何对点P1和P2的最小距离ηij,P1=(x1,y1)是块体的i的一点,而P2=(x2,y2)是块体j的一点,如图3-1所示。
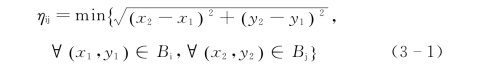
式中,符号∀为“对全体”;Bi和Bj分别代表块体i和块体j的所有点,如图3-1所示。根据式(3-1)的距离定义,只有当ηij=0时块i与块j是接触或重叠的,否则ηij>0。(https://www.xing528.com)
由式(3-1)很明显,如果距离η大于所有块体点的距离ρ的两倍,即ηij>2ρ,则对块体i和块体j在下一步时间内不可能相碰。
用式(3-1)不可能计算两个块体间的距离,因为一个块体就有无限个点。定义距离的式(3-1)可写成对计算更有效的形式
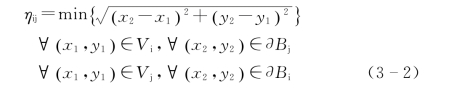
式中,∂Bi及∂Bj分别是块体i与块体j的边界段;Vi及Vj分别是块体i与j的顶点。图3-1表示依据式(3-2)的距离的含义。式(3-1)和式(3-2)是在两个块体不相重叠情况下的等式。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




