变形量分为绝对变形量与相对变形量。绝对变形量是指各期观测相对于首期观测的变形量,又称累计变形量。相对变形量一般是指观测点相邻两期观测的变形量或相邻点变形量的差值(变形差),又称观测点本次变形量和相邻点相对变形量。变形量与对应观测时间段的比值称为变形速率。对于变形观测而言,相邻点相对变形量的大小会影响建筑物内部结构的变化,是设计、施工和管理单位都非常关心的一项重要技术指标。若建筑物有要求精度较高的外部连接设备时,则绝对变形量也是一项重要的变形指标。
1.观测点的绝对、相对变形量
以沉降观测为例,设观测点A的首期观测高程为
第i、j期的高程分别为
则该点第i期的绝对沉降量
和本期至第j期的相对沉降量
为
若观测点B与点A相邻,且在建筑物的同一轴线上,还需计算同期(如第i期)、第i期至第j期两点的相对沉降量(如
也称累计、本次相对沉降量,即
表15-5给出了某建筑物相邻柱基础观测点A、B的绝对变形与相对变形观测成果。
表15-5 某建筑物观测点A、B沉降观测成果
续表(www.xing528.com)
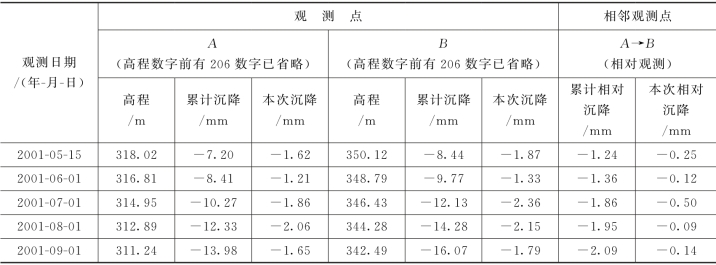
图15-10 挠度计算
当同条轴线上有3个以上观测点时,还可计算中间各点的挠度。如图15-10所示,设中间点C第i期的挠度为δ,第i期至第j期的挠度为δ′,则
式中:LA、LB为观测点C至观测点A、B的水平距离。
2.变形过程线
为了更清晰、直观地描述观测点的变形,经常需要绘制观测点的变形过程线。其是以时间为横坐标,以累计变形(沉降、倾斜、位移等)为纵坐标绘制的曲线。在选用坐标轴尺度时,应依据观测时间长度和累计变形值综合考虑,尤其是纵坐标应选用整数比例尺,以便于量取变形值。变形过程线可用折线表示,也可拟合成样条曲线表示。如图15-11所示,A、B点的沉降过程线,便是依据表15-5中观测点A、B的累计变形值绘制的。
图15-11 观测点变形过程线
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
