【摘要】:而直线超高为0,圆曲线超高为h,等级铁路、公路需要在转向处插入缓和曲线,以使超高由0渐变至h。缓和曲线可采用回旋线、三次抛物线、双纽线等线形。目前,我国道路系统常采用回旋线作为缓和曲线。任取一点P(x,y),其微分弧段d l在坐标轴上的投影分量为将上式积分,并略去高次项可得x、y以l为参数的方程,即缓和曲线的参数方程为当l=lS时,缓和曲线终点的坐标为
车辆在曲线上行驶会产生离心力,需要用外侧超高的方法克服离心力。而直线超高为0,圆曲线超高为h,等级铁路、公路需要在转向处插入缓和曲线,以使超高由0渐变至h。
缓和曲线可采用回旋线(亦称辐射螺旋线)、三次抛物线、双纽线等线形。目前,我国道路系统常采用回旋线作为缓和曲线。
(一)缓和曲线的主要公式
1.基本公式
如图11-14所示,回旋线上任一点的曲率半径ρ与曲线的长度l成反比,即
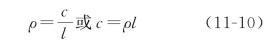
c值可按以下方法确定:缓和曲线与圆曲线连接时,ρ=R,此时的l为缓和曲线的全长lS,即l=lS,将其代入至式(11-10)中,得c=RlS。而lS要依据c值确定,目前我国公路采用c=0.035V3(V为计算行车速度,单位km/h),则lS=0.035V3/R。
2.切线角公式
如图11-14所示,设回旋线上任一点P的切线与ZH(或HZ)点切线的交角为β,则P处微分曲线弧段所对的中心角dβ为

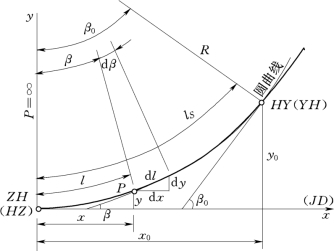
图11-14 缓和曲线(https://www.xing528.com)
对上式积分得

当l=lS时,整条缓和曲线的切线角(亦称缓和曲线角)β0为
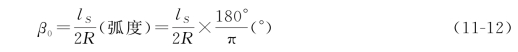
(二)缓和曲线的参数方程
如图11-14所示,建立直角坐标系:ZH(或HZ)点为原点,过该点的切线方向为x轴,向径方向为y轴。任取一点P(x,y),其微分弧段d l在坐标轴上的投影分量为

将上式积分,并略去高次项可得x、y以l为参数的方程,即缓和曲线的参数方程为

当l=lS时,缓和曲线终点的坐标为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




