【摘要】:故式可近似地写成由m=±,代入上式整理,得式即为等精度观测时用观测值的改正数求观测值中误差的公式。由图可见,当m不变时,mx随着n增大而减小,但当观测次数达到一定数值后,中误差的减小逐渐缓慢,所以,为了提高观测结果的精度,除了适当增加观测次数外,还必须选用相应精度的观测仪器和适当的观测方法,才能获得最经济的效果。
1.单位权中误差
等于1的权称为单位权,权等于1的观测值中误差称为单位权中误差。设单位权中误差为μ,则权与中误差的关系为

如μ=m1时,p1=1,即l1的中误差m1称为单位权中误差。
由式(6-30)可写出单位权中误差与观测值中误差的关系式如下。
![]()
得
![]()
所以
![]()
当n→∞时,用真误差Δ代替中误差m,衡量精度的意义不变,则可将上式改写为

式(6-31)为用真误差计算单位权观测值中误差的公式。类似式(6-20)的推导,可以求得用观测值改正数来计算单位权中误差的公式为

式中:v为观测值的改正数;n为观测值的个数。
2.加权平均值中误差
由式(6-27)得(https://www.xing528.com)

按中误差传播定律,加权平均值x的中误差如下:
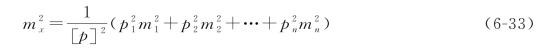
式中:m1,m2,…,mn为相应观测值的中误差。
将式(6-30)代入式(6-33),得

则
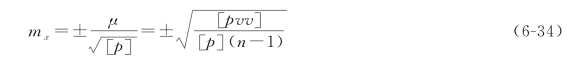
【例6-7】 对某一角度,采用不同测回数,进行了4次观测,其观测值列于表6-4中,求该角度的观测结果及其中误差。
解:计算过程及计算结果列于表6-4中。
表6-4 不同精度观测最后结果及其中误差计算表


该角的最后观测结果为63°44′59″±2.2″。
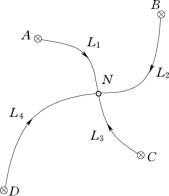
图6-8 单结点水准路线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




