地面点的高程及高程基准系统说明

我国国家大地坐标系——1954年北京坐标系和1980年西安大地坐标系均属于二维坐标系,不包含明确的点的高程信息。而随着卫星定位技术的发展,GPS 定位技术广泛应用于各行各业,其带来了测量作业方式的根本性变革。

（一）高程系统

测量常用的高程系统有大地高系统、正高系统和正常高系统。

1.大地高系统

大地高系统是以地球椭球面为基准面的高程系统。大地高的定义是,由地面点沿通过该点的椭球面法线到椭球面的距离。大地高也称为椭球高,一般用符号H表示。

大地高是一个纯几何量,不具有物理意义。同一个点,在不同的基准下,具有不同的大地高。利用GPS定位技术,可以直接测定观测站在WGS-84中的大地高。

2.正高系统

正高系统是以大地水准面为基准面的高程系统。正高的定义是,由地面点沿通过该点的铅垂线至大地水准面的距离。正高用符号Hg表示。

正高有完整的物理意义,对于测量来说意义重大,但无法精确测量出来。原因是引力常数无法确定,也就是重力加速度g未知。每个地方的引力常数无法精确测量,于是人们设想地球均质,便可计算出重力加速度γ,即引入了一个跟大地水准面极为类似的面,这就是似大地水准面。

3.正常高系统

正常高系统是以似大地水准面为基准面的高程系统。正常高的定义是,由地面点沿通过该点的铅垂线至似大地水准面的距离。正常高用Hr表示。

似大地水准面严格说不是水准面,它是拟合出来的大地水准面的最或然值,是用于计算的辅助面。它与大地水准面不完全吻合,差值为正常高与正高之差。研究证明,似大地水准面与大地水准面在海洋上是重合的,仅在地面上略有不同,在山岭地区相差有1～3m,而在平原地区相差不过有几个厘米。我国的国家高程测量采用正常高系统,国家高程点的高程是正常高。

4.高程系统之间的转换关系

如图1-6所示,大地水准面到地球椭球面的距离,称为大地水准面差距,记为hg。大地高与正高之间的关系可表示为

似大地水准面到地球椭球面的距离,称为高程异常,记为ζ。大地高与正常高之间的关系可表示为

大地高、正高、正常高均可用于工程测量。通常,由于某种技术原因,在一般实际应用中采用正常高或正高,不用大地高。在要求不高时,往往忽略hg、ζ,不再有大地高、正高、正常高的区别。(www.xing528.com)

图1-6　高程系统间的相互关系

（二）地面点高程的表示

1.国家高程基准

我国在山东青岛设验潮站,收集的1950—1956年的验潮资料,推算的黄海平均海水面作为我国的似大地水准面,并在青岛市观象山建立了水准原点。水准原点到验潮站平均海水面高程为72.289m。这个高程系统称为“1956 年黄海高程系”。由于海洋潮汐长期变化周期为18.6年,20世纪80年代初,国家又根据1952—1979年青岛验潮站的观测资料,推算出新的黄海似大地水准面作为高程零点。由此测得青岛水准原点高程为72.2604m,称为“1985年国家高程基准”,并从1985年1月1日起执行新的高程基准。

综上所述,由于正常高高程系统为我国法定的统一高程系统,且在我国境内各点的高低可通过其正常高唯一确定,因此,在不特别指明的情况下所讲的高程即指正常高。

2.地面点高程表示

地面点到大地水准面的铅垂距离称为绝对高程,又称海拔。如图1-7中A、B两点的绝对高程分别为

当个别地区引用绝对高程有困难时,可采用假定高程系统,即采用任意假定的水准面为起算高程的基准面。图1-7中,地面点到某一假定水准面的铅垂距离称为假定高程或相对高程,用H′表示。例如,A、B的假定高程(相对高程)分别为。

图1-7　高程和高差

3.高差

地面上两点间高程之差称为高差,一般用h加起止点作下标表示,见图1-7中A、B两点的高差为。

可见两点间的高差与高程起算面无关。

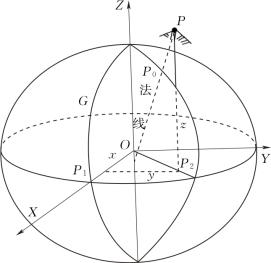
图1-8　空间直角坐标系