确定核动力装置重要阀门可靠性：通过少量样品试验得出结论

由于核动力装置上所用公称尺寸较大的重要阀门一般造价很高，且出厂批量小，所试验阀门的数量一般也较少。因此为计算它们的可靠性指标，要求采用只能限于少量试验样品的方法，它在少量试验样品（不少于4台、不多于23台）和具有推断性信息的基础上可以确定出工作时间的分布规律。这种方法是供具有可靠性高（P＞0.95）的阀门用。

对类似产品和部件进行类似的试验，由此而得到的可靠性指标的数据，可以作为推断性信息。凡在结构上与试验阀门相似的产品或部件，其计算的可靠性相同，即使其中有少量的零件有所不同，但它们比试验阀门中的相应部件具有更高的可靠性。在这些条件下，这些产品或部件即可认为与试验阀门类似。这个方法对于可恢复和不可恢复的两类阀门都可运用。

属于推断性信息的有：

1）T^a_i——与过去试验过的类似产品的无故障工作时间；

2）m^a——本次试验时的故障数量；

3）F_a（T）——工作时间的分布规律；

属于经验数据的有：

1）T^a_i——试验过的产品无故障工作时间；

2）m^∂——多次试验的故障数量。

对经验数据（产品试验结果）进行处理，并参考推断性信息（有关类似产品的数据）可确定无故障工作时间的分布规律和保质期内无故障工作的概率。

为确定工作时间的分布规律，运用推断—经验函数法，这时推断性信息数据是借助于称作核算曲线得出的。给出工作时间的推断分布规律F_a（T）或相似的阀门的工作时间数列T^a_i。如果预先不确知F_a（T），则它可按T_i值的数据画出图形。经验数据可写成产品工作时间T_i的数列的形式。

为了确定推断性信息的比值，应算出推断性分布的可信性系数

ω=m^a/（m^a+m∂）

0≤ω≤1

然后确定推断性数据分布和经验数据分布的工作时间分布区域的范围[a，b]，这里a和b是两列数据T^a_i和T^∂_i工作时间的最小值和最大值。例如：

T^a_i=35、72、94、110、242；

T^∂_i=27、31、81、115、139；

这时a=27，b=242。

如果a和b是未知数，而推断性信息是以工作时间分布函数的形式F_a（T）给出的，立时取a=0、b=T^a_c+3S或b=T_c^∂+4S，这里：

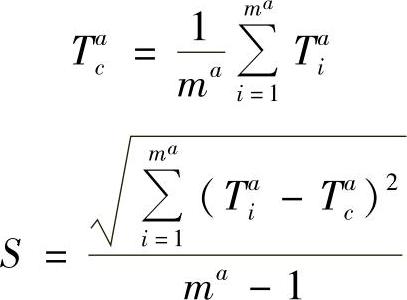
接下列方程式画出核算曲线，当预先给定F_a（T）时，核算曲线是按表12-8所给的数据来建立的。(www.xing528.com)

表12 - 8 核算曲线辅助表

在该表上T^a_i在第一栏写一次，不重复；

n^a_i为实现相应于第一栏内所列数值的次数，放入第二栏；

累积次数H_i=n₁+n₂+n_i放入第三栏；

比值H_i/m^a=F_a（T_i）放入第四栏；

放入第五栏内的是：Y_i=ωF_a（T_i）。

并按它的值划出第1条核算曲线。当F_a（T）已知时，可利用列有T^a_i和Y_i值的表（见表12-9）。

表12 - 9 T^a_i和Y_i值

在第一栏写下20～30个T^a_i的任意选取的值。它们是从a到b区段内等间隔分布的；在第二栏内写下Y_i=ωF_a（T_i）的值。

在坐标纸上按下列各线的交点画出核算曲线F_a（T_i）。沿横坐标截取表12-9所给的T^a_i的值，沿纵坐标截取Y_i的值。把所有交点连成折线，就是核算曲线F_a（T）。

每次实现经验分布函数时的增量按下式确定：

δ=（1-ω）/m²

在已建立的线图上沿横坐标轴从a到b画出的各曲线Y_i，相互i间具有等高δ。这些曲线具有表征推断性分布函数F_a（T）的核算曲线的形状。从横坐标轴向上属的第一条线通过A（a、O）点和C（b、ω）点，如图12-1所示。其余的曲线平行于第一条线，其间距分别为δ、2δ、3δ、…、lδ，这里l为不同T^a_i值的数目。最后一条线应通过B（b，1）点。在横坐标轴的T^a_i±Δ/2各点上引出垂直线（这里Δ为T^a_i值的测量精确度）。找出T_i-Δ/2点上的垂线与第i条曲线的交点以及T_i+Δ/2点上的垂线与第i+1条曲线的交点。用折线将A（a，O）点到B（b，1）点之间的所有交点连接起来，见图12-1。

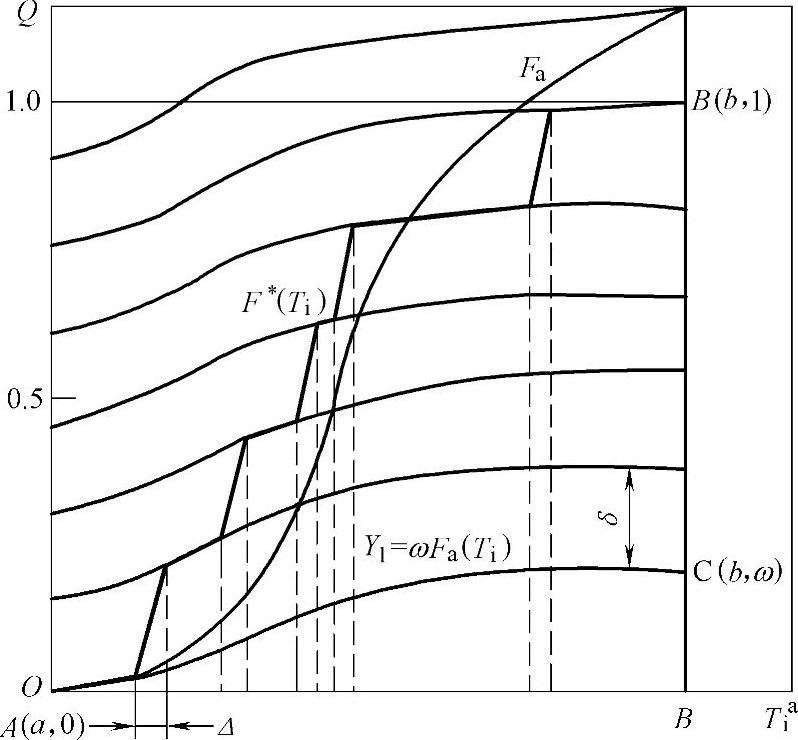
图12-1 核算曲线

借助于图线可以确定在保证循环次数T_T内的故障概率Q。为此，从（T_r、O）点作一条垂直于横坐标的垂线与折线F∗（T）相交，从交点作一条直线平行于横坐标。这直线与纵坐标相交，其交点确定所要求的保证循环次数T_T内故障概率Q，在保证循环次数内无故障工作的概率P=1-Q。这样一来，获得的P（T_T）不小于P。

当工作时间的分布规律是正态分布或可以当作正态分布时，对于不可恢复阀门少数量（少于20）观查的结果，可以根据前苏联部颁标准ОСТ 26-07-862进行处理。当只根据不多于6台阀门的试验结果确定可靠性指标时，应于完成观测后在阀门的实际运行条件下进一步修正可靠性指标。