不可恢复阀门可靠性指标的计算

根据对试验样品或按定型工艺制造的产品的测定试验结果，确定所有产品平均故障间隔的分布规律，为此必须用足够数量的产品（约50）试验其可靠性。也可以对产品进行数量较少的试验，但不少于6台，这时平均故障间隔的分布规律认为是正态分布。

为了确定不可恢复阀门的可靠性，可利用下列指标：具有置信限的退役前平均寿命T_p·cn和保质期内无故障工作概率P（T_T）（置信下限）或要求的循环数。产品在试验过程中不容许进行修复。

可靠性指标是按正态分布规律来计算。阀门退役前的平均寿命按下述公式计算：

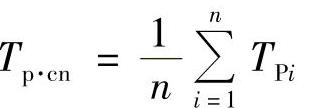
式中 T_Pi——第i个样品首次故障前的平均工作时间；

n——试验样品的个数。

当没有出现故障时，则采用产品停止试验时所用去的工作时间。

退役前平均寿命的均方离差按下式计算：

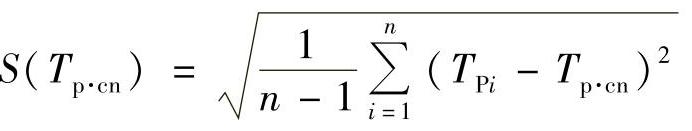
在没有出现故障的情况下，采用T_p·cn=T_pi，但不少于1000次循环。为了确定离散值（在每一组选取中不应大于一个离散值）利用绍维涅准则。小于T_p·cn的离散值不允许排除。当利用绍维涅准则时应研究以下不等式：

T_Pi^-Tp·cn＞τщ^S（T_p·cn）

式中 T_Pi——T_P的离散值；

τщ——绍维涅系数，见表12-5。

如果不等式成立的话，则T_Pi值被排除，用等于T_p·cn的值来替代，然后再确定本批抽样中的T_p·cn和S（T_p·cn）的值。

退役前平均寿命T_p·cn的置信下限按下式计算：(www.xing528.com)

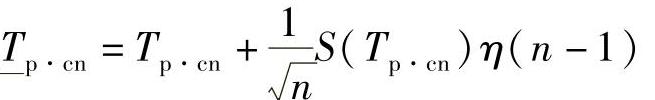
而置信上限按下述公式计算：

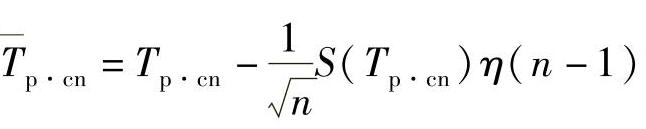
式中 n——参与试验的样品数；

η（n-1）——标准化参数，见表12-6。在保质期内无故障工作概率P（T_pγ）的置信下限按下式确定：

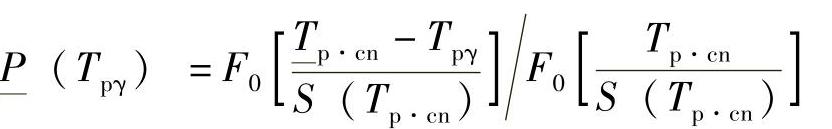
式中 F₀（x）——表12-7给出的函数；

T_pγ——γ%保质寿命（在技术任务书中规定的保质期内寿命）。

如果T_p·cn/S（T_p·cn）＞3，分母可取1。

表12 - 6 η（n-1）的值

注：α为置信概率。

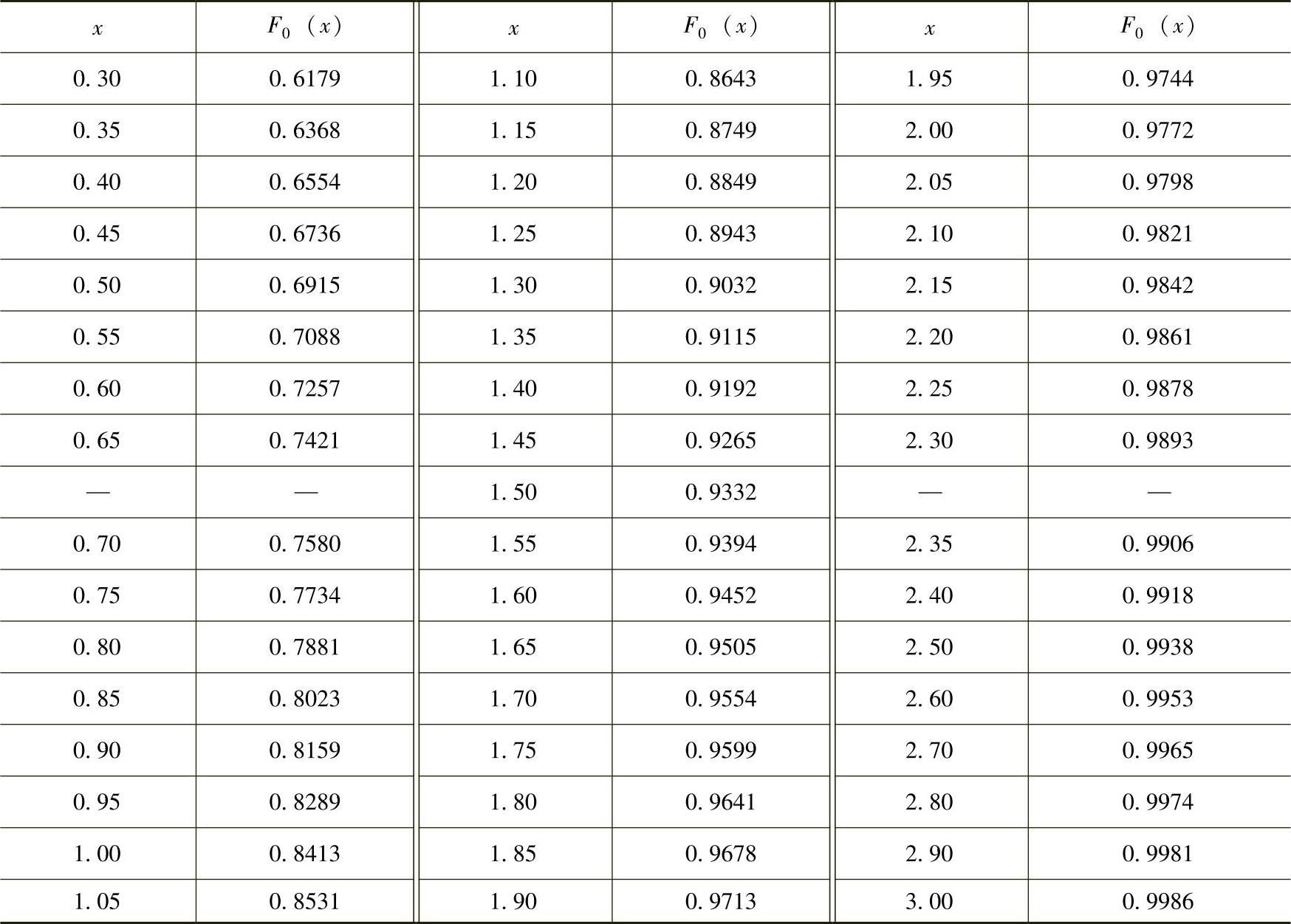
表12 - 7 函数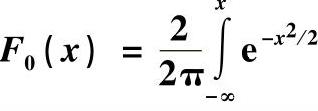dx的值