对试验样品或按定型工艺制造的并属于可恢复阀门的产品进行测定试验,在试验结果的基础上找出产品无故障工作时间和恢复时间的分布规律。无故障工作时间取决于工作循环数或出现首次故障前和依次发生的故障之间的以小时(h)计算的工作时间。恢复时间就是排除故障所需要的时间。为了建立分布规律,试验时的故障数(或有关恢复时间的数据)应不少于24个。
可靠性和维修性指标是在取得无故障工作时间Tpi、恢复时间ti、故障数m和试验时的总工作时间TΣ的基础上计算出的。当进行试验时,发生故障的产品要修复好。同时也要进行在技术任务规定的范围内的日常维护工作(必要的调整、加润滑剂、拧紧填料函螺栓等),同时只允许用该产品所规定的备件和附件。这些工作的范围仅限于试验计划的规定内容。排除引起故障的缺陷所需要的时间和无故障工作时间均应在试验记录上记录下来。
为了确定分布规律,建立一个包含无故障工作时间的变分级数值和恢复时间的变分级数值的辅助表,然后在相应的坐标纸上画出图形。判定所得到的试验分布接近哪一种理论分布规律:指数分布、正态分布以及其他的分布。为此,按某一个符合准则进行比较,能保证最佳相符情况的理论函数,即认为适合于这批试验取得的分布规律。
下面给出在指数分布规律情况下确定可靠性指标的公式。平均故障间隔:
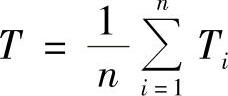
T值的置信下限:
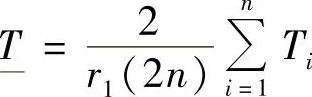
T值的置信上限:
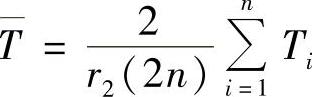
式中 n——故障次数;
Ti——无故障工作时间(或循环数);
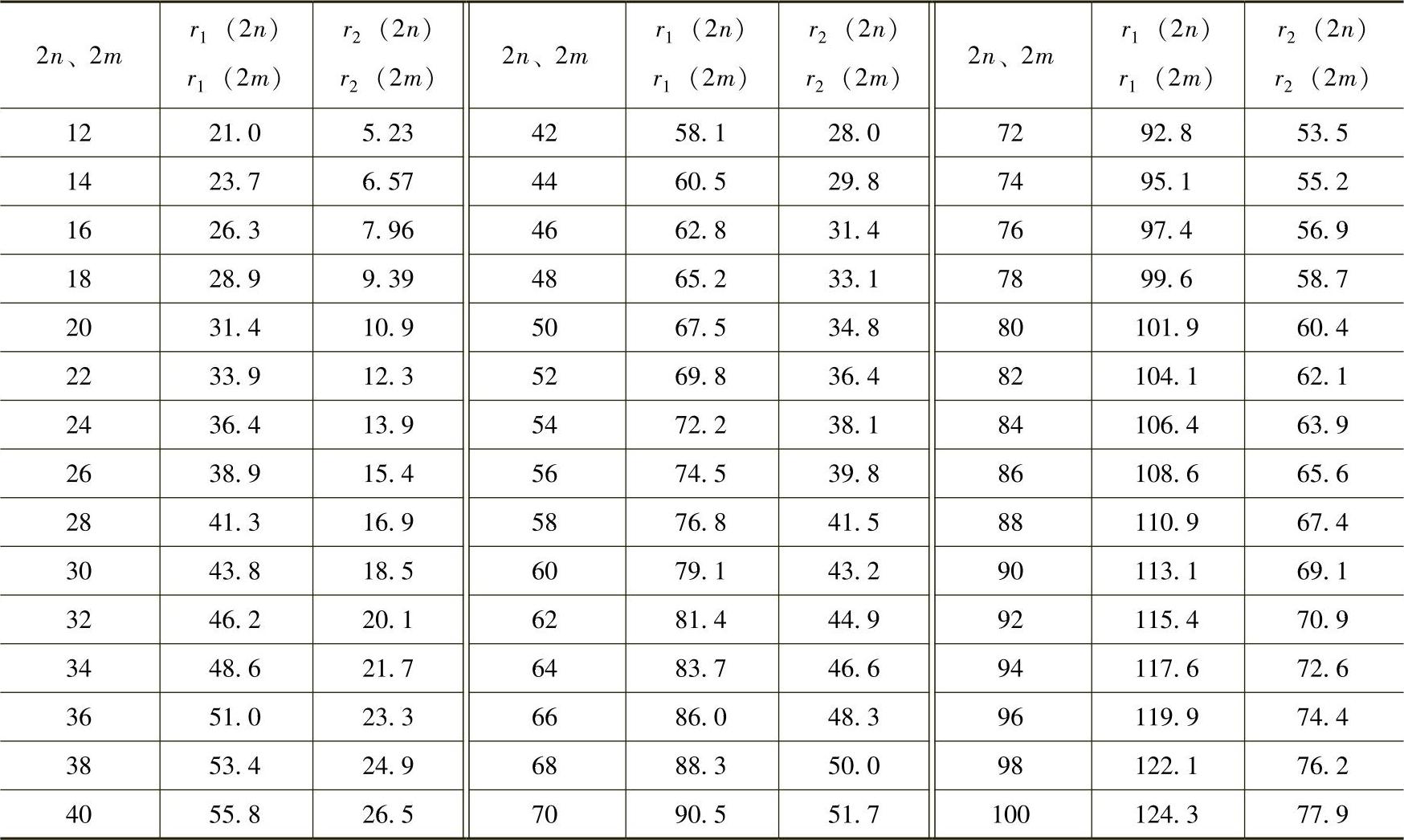
r1(2n)、r2(2n)——根据表12-4来确定的系数。
由此可见,平均故障间隔的范围如下:
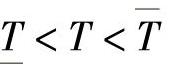
同样按这些公式计算首次故障前的平均工时间Tcp,它的置信下限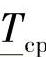 和置信上限
和置信上限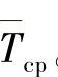 。只
。只
是式中符号的意义有所改变:
式中 n——出现首次故障前的试验产品数;
Ti——第i个产品故障前的工作时间;
r1(2n)、r2(2n)——系数,见表12-4。
表12 - 4 系数r1和r2
故障率
λ=1/T
式中 T——平均故障间隔。
故障率的置信上、下限按下式计算:
 (https://www.xing528.com)
(https://www.xing528.com)
在保质期内无故障工作的概率:
P(TT)=exp(-TPγ/T)
式中 Tpγ——保质期内的γ%概率寿命。
如果将公式中的T替换上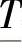 和
和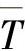 的话,则可相应地确定置信度的下限和上限。
的话,则可相应地确定置信度的下限和上限。
当处理试验数据时应排除离散数值(在每一组选取中不能多于一个这种离散值)。评价时可以利用绍维涅(щовене)准则,且小于T的离散值不应排除。当利用绍维涅准则时,要研究不等式:
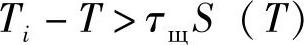
式中 Ti——离散值;
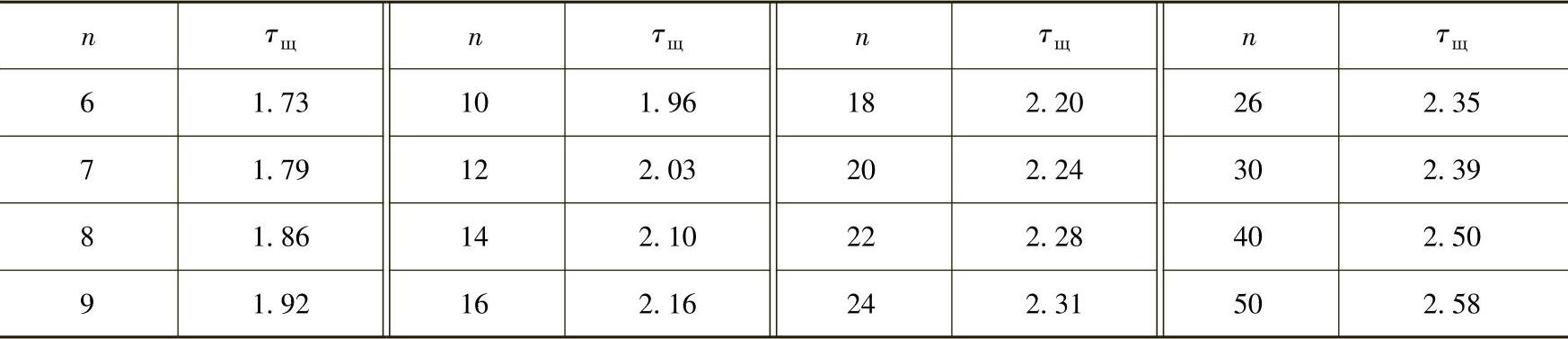
τщ——绍维涅系数,见表12-5;
S(T)——平均故障间隔的均方离差。
如果不等式成立,则Ti值被排除,替代它的是T值,然后对这种抽取样品,重新确定T和S(T)值。即
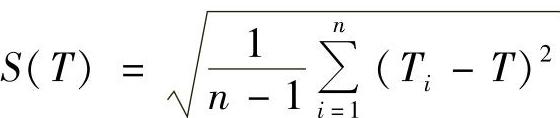
式中 n——故障次数。
表12 - 5 τщ的值
恢复时间的分布服从指数规律时,可恢复阀门的维修性指标可按下列公式来确定。平均恢复时间
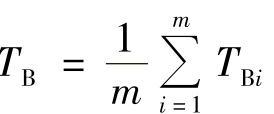
平均恢复时间的置信下限
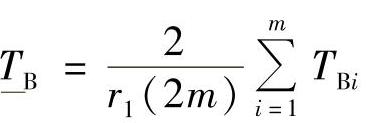
平均恢复时间的置信上限
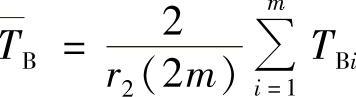
式中 TBi——恢复时间;
m——记测恢复时间的数目;
r1(2m)、r2(2m)——根据表12-4确定的系数。
由此可见,平均恢复时间的置信限
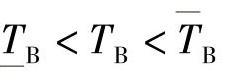
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




