如何评价设计阶段阀门的可靠性？

产品的可靠性可在阀门设计、制造、试验和运行的不同阶段都可予以评价。试验方法和所获得信息的处理都不同。设计、测定试验、检查试验、运行是主要阶段。

在设计阶段决定产品可靠性的任务是在分析结构和运用可靠性统计数据的基础上，建立可靠性参数。起决定性作用的是阀门结构上工作零件的数量、它们的相互作用、形状上是简单还是复杂、零件的材料、它的工艺可靠性、有效应力和强度系数、可能的超载、有无可避免发生事故的联锁装置、有无安全装置、有无阀门的行程指示、工作强度和温度、压力工况等。

计算是以单个的构件工作可靠性的统计数据为基础的，并一次性完成，故障的分布定理并不清楚，需采取某种假设。根据对各个构件及整体设备所得出的数据及其可靠性评价，确定出措施，以使新设计的结构能达到所要求的参数，并决定是否需要对结构方案进行适当的修改，然后比较各个结构方案的可靠性指标，并做出评价。在设计阶段的可靠性计算只是粗略的，因为它不是以具体的试验结果为依据，而是假定组成被研究产品构件的可靠性与其他现有产品并进行过评价和分析以及进行过试验的阀门构件相类似。

为了简化计算，产品可认为是不能或不必恢复的阀门，因此属于不可恢复类。故障率认为是常数，而各个构件无故障工作的概率服从指数定理。如果对于某个构件实验证实使用其他定理更准确，即可进行一定的修正。

为了定量地评价阀门的可靠性，采用产品在保质期内无故障工作的概率时，不考虑产品在仓库内的存放。当仓库存放的条件影响到阀门的构件（橡胶膜片和橡胶环、电气控制线路上的复杂元件等）的可靠性时，则阀门的可靠性应将仓库的存放考虑进去。

计算可靠性的原始资料有产品加工图、有关产品可能出现的工况数据（温度、压力等）和工作循环期数据、保质期、保质期内γ%概率的寿命和产品在保质期内可能处于开启状态及关闭状态的寿命（均以百分比表示）。采用手动控制也不能认为是完美的备用手段，它只是改变了故障的特点而已。因此阀门可以看作是由串联连接的部件所组成，而部件又视为由串联连接的零件所组成，而且这里只考虑那些失效可造成产品故障的那些零部件。

阀门无故障工作的概率可按下式来确定：

P=P₁P₂P₃…P_n

式中 P₁、P₂、P₃、…、P_n——各部件无故障工作的概率。

确定在运行过程中部件内不同构件的工作条件，查明工作在相同条件下的构件，对于这些构件取相同的故障率。始终处于载荷下的构件（壳体、启闭件等）按整个保质期T_T计算。对于仅在工作循环时间内承受载荷的构件，按指定的γ%寿命计算完成循环的总时间：

T_narp=ntn

式中 t_n——一次工作循环期；

n——考虑到γ%概率的寿命的工作循环次数。

当阀瓣开启时承受载荷的构件，假定每个循环时间按200s计，其总开启时间

T_y，o=200n

当阀瓣关闭时承受载荷的构件，应计算阀门保质期与阀瓣总开启时间之差

T∂=T_T-T_y

故障率按下式决定：

λ=aλ_n

λ′=bλ

式中 λ——受力构件的故障率；

λ′——非受力构件的故障率；

λ_n——构件的标准故障率（从表12-1中选取）；(www.xing528.com)

a——考虑到构件运行条件的系数，壳体、法兰、垫片、密封件a=1；阀瓣的密封件

a=2；导向件、螺纹连接件、液压和气动元件a=5；

b——考虑到非受力构件故障率减少的系数。对于非受力机械构件、液压和气动元件

b=1×10^-4；对于电气设备（电动机、自整角机、变压器、扼流圈、电容器、

电位计、测量仪表）的非受力元件b=（2.0～2.5）×10^-4；对于继电器、转

换开关和插塞接头b=1×10^-3。

在保质期T_T内处于载荷下的部件无故障工作概率，按下式计算：

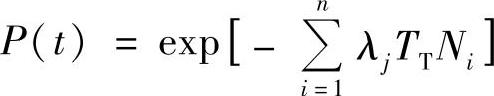
式中 N_i——第i类型构件的数目；

n——构件的类型数。

仅仅在工作周期内处于载荷下的部件无故障工作的概率，按下式确定：

在某段时间T内不受力的部件无故障工作的概率，按下式计算：

对具体阀门结构的构成拟出逻辑框图，对其进行分析，结果即可求出此产品无故障工作的概率。

表12 - 1 阀门某些构件和部件的故障率^①

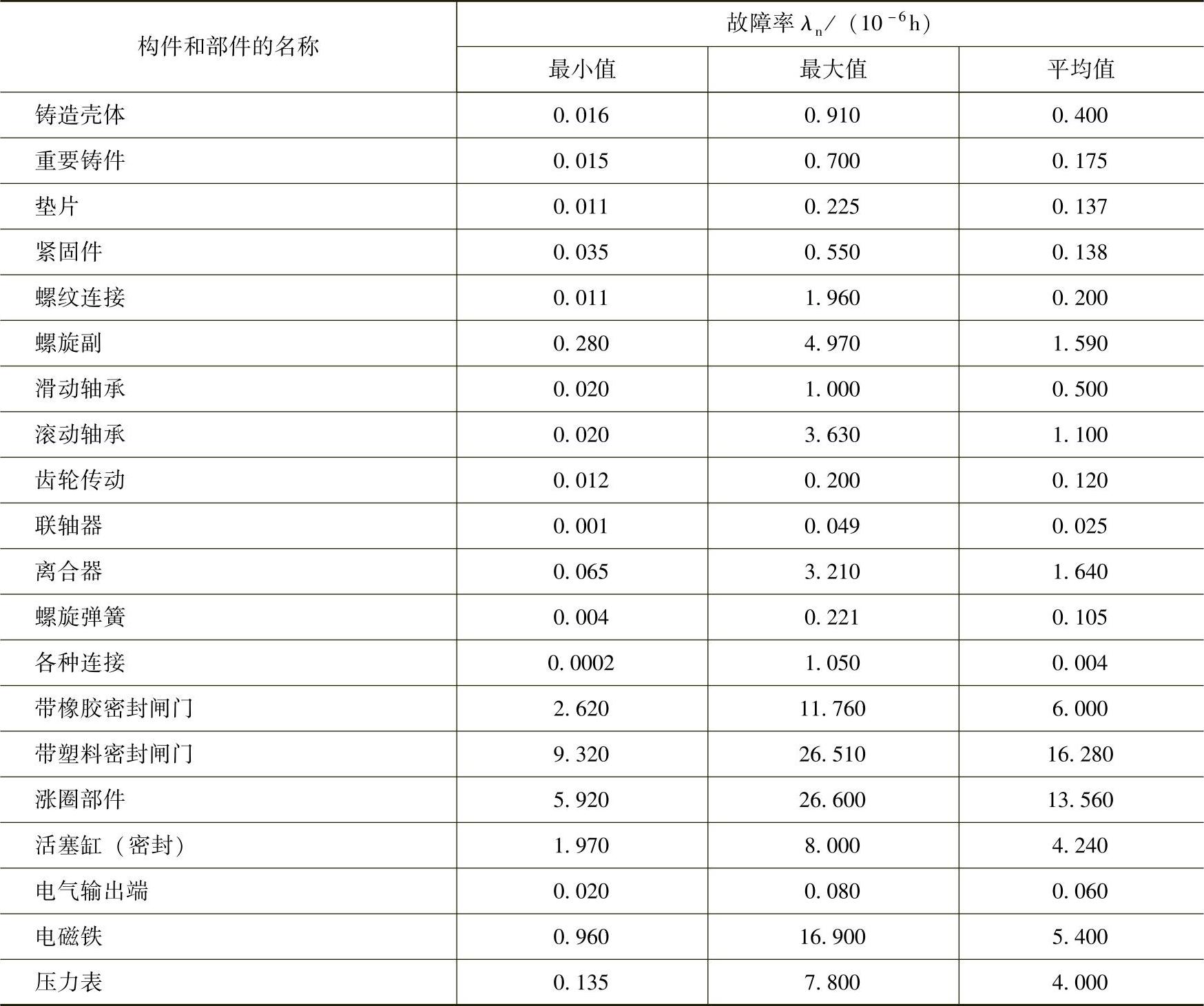
① 在产品的工作条件不恶劣和保质期短的条件下，λ_n采用最小值，当工作条件恶劣和保质期长的条件下，λ_n采用最大值。

由于上述可靠性是基于若干故障率的近似值计算出来的，因而，在此阶段计算得出的无故障概率还不能当做本产品的可靠性参数来用。这些结果，只能用以确定各种结构方案可靠性的近似值或进行相互比较的目的。为了粗略估计各种阀门的故障率，可以运用表12-2中给出的不同用途阀门的故障率。这些数据是美国在1961～1963年试验时取得的。

表12-2 阀门的故障率