轴向对称圆柱形零件的热疲劳计算方法

在圆柱形零件的壁厚温度变化过程中，当冷热变换时在圆筒上产生热应力。零件的材料在不失去强度时能经受一定的循环数。它与筒壁内产生的弹塑性变形有关。靠计算来确定给定应力范围下的许用循环数或给定循环数下的许用应力范围。沿筒壁厚度的温度分布采用线性定律：

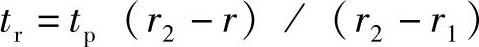
式中 t_r——在半径为r点上的温度（℃）；

t_p——内外壁温度差（℃），t_p=t₁-t₂；

t₁——内壁面上相应的温度（℃）；

t₂——外壁面上相应的温度（℃）；

r₂——圆筒的外半径（mm）；

r₁——圆筒的内半径（mm）。

假定下列条件：相对于圆筒轴的径向温度场对称，沿圆筒的长度上温度场为常数。在温度作用下离圆筒两端足够远的截面仍保持平面。轴向应变ε₂假定为常数。求温度差和介质压力作用下的折合应力。在圆筒上作用着下列周向和切向应力：

式中 μ——泊松数；

α——温度线胀系数（1/℃）。

在内壁面上由介质压力而产生的应力

式中 k——圆筒内外半径之比，。而在外壁面上

轴向应力

圆筒内壁、外壁面上的总应力按下列公式确定：

式中 、——圆筒内外壁面上的径向热应力（MPa）。

根据标准，折合应力按第三强度理论——最大切应力理论（除脆性破裂情况外）来确定。按照该理论，强度条件为σ₁-σ₃≤[σ]。当计算塑性材料时，应用第四强度理论，具有强度条件为

式中 σ₁、σ₂、σ₃——主应力，σ₁≥σ₂≥σ₃。(www.xing528.com)

当计算圆筒内壁面A点上或外壁面B点上的折合应力和时，采用总应力的相应值作为主应力。依据和的值，确定在一个热循环内，在载荷最大的材料纤维所研究截面上的最大折合弹塑性变形。对于这些具有最大拉应力和最大压应力的点，计算出和的比值，此处σ_SA、σ_SB为相应于A点和B点处温度的屈服强度，并要确定在这些点上的最大应变、，因为这些点处于材料塑性变形的最危险区。利用下列公式：

式中 E_A、E_B——材料在点A和点B处相应温度下的弹性模量（MPa）。

当条件折合应力不超过屈服极限时，变形认为是弹性的，否则就是弹塑性的。因此，当时，应变量Δε取其条件弹性应变量：；当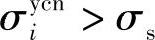时，折合弹塑性应变量会增大到它的1～1.5倍，这要视压力而定。在热疲劳条件下工作的零件寿命用断裂前的当量循环数来确定

式中 N_p——当量循环数；

a、b、A——阀门系数，a=0.352，b=0.224，A=3.82；

τ_n——平均循环期，τ_n=τ/N；

式中 N——在装置整个工作期间τ内预期的热循环数，考虑到安全系数η（采用η=20）时的许用热循环数N_B=N_p/η。

许用机械应力借助于许用载荷曲线计算，如图4-21所示。这曲线是按照下述方法建立起来的：划出cd线，点c是循环期内最大弹塑性变形量的极限值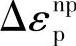的百分数来确定，这时金属由于单纯循环热负荷而开始断裂

点d相应于装置运行的整个工作期τ内，在零件最大工作温度下材料的持久强度极限。

然后建立ef线，线上的点e相交于在循环期内最大许用弹塑性应变量

式中 X——应变安全系数，X=η^a，当η=20，a=0.354时，X=2.9。

图4-21 许用载荷曲线

在f点，当装置在最大工作温度时的[σ]_max

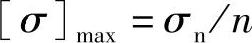
式中 σ_n——在装置整个工作期τ内，在最高温度下的金属持久强度极限（MPa）；

η——安全系数（由设计者选取）。

三角形0ef是考虑到综合应力的作用下在最大给定温度下的材料安全工作区。在这个区域限度内，可以选择循环期内最大许用弹塑性应变量和作用于装置整个工作期内不变许用机械应力的各种组合。应当指出，循环期内许用折合应变量Δε_n包括循环期内由于单纯循环应力而产生的应变量和由于热膨胀未能完全补偿而产生的应力应变量两部分。

同样应满足下列条件：由未完全补偿热膨胀和不变机械载荷而引起的总条件折合应力在任何可能的零件工作温度下应小于相应温度下两个热循环之间的平均循环周期τ_n内的屈服极限和蠕变极限。