阀门零件强度验算方法

验算是在阀门元件的基本尺寸确定后，考虑到全部设计载荷时，根据图样上给出的制造尺寸来进行。需要验算的零件图应包括：工艺上过渡半径必须修正的尺寸；衬套、垫圈下的结构凸台半径必须修正的尺寸；以及考虑到所采用的管子和钢板品种在内的类似零件。验算采用“标准”中的“计算和实验确定应力、应变、位移和作用力的通用方法”一节内给出的步骤。对于未包括在这种步骤内的那些条件，则采用阀门设计上所使用的计算步骤，而在重要的情况下，应采用专门制定的并得到有关权威机构批准的步骤。

需要验算的零件可以看作由圆柱形壳体、球形壳体或其他形式的壳体以及圆形板、环形零件和诸如此类的简单元件所构成。它们可以根据薄壁或厚壁和薄板或厚板理论来计算。这些元件之间的连接以相应的力、力矩和压力的作用来替代，因此要确定所验算的元件内的应力、应变、位移和作用力。

一回路内的主切断闸阀起着非常重要的作用，并具有较大的公称尺寸，一般为DN500～DN800。应对它的工作条件进行非常仔细的分析，并进行认真的计算。安装在辅助回路的管线上的公称尺寸较小的截止阀和其他类型的阀门，可以用一般在阀门设计上所采用的方法进行计算；安装在非放射性的饱和蒸汽与新鲜蒸汽以及给水管线上的阀门，可以根据介质的动力参数、公称尺寸和它们的功能来选择阀门的计算方法和范围。但首先要满足阀门设计标准的要求。

下面举例来研究两种结构的闸阀阀体和两种结构的闸阀阀盖分解成组合元件的程序进行的强度验算，如图4-14～图4-17所示。

计算应用下列符号：

p——计算内压力（MPa）；

N——单位长度上的纵向力（N/mm）；

H——在接头处单位长度上的剪切力（N/mm）；

F_oc——管道的轴向力（N）；

w——壳体的径向位移（mm）；

M_n——在接头处单位长度上的弯矩（N·mm）；

u——圆环或圆板的径向位移（mm）；

w^t——因温度而引起的截面位移（mm）；

θ——元件的转角（rad）；

φ₀——球形扇面半张角（°）；

σ_z、σ_θ、σ_r——相应于圆柱形壳体的纵向、环向和径向应力（MPa）；

R_i——第i元件的平均半径（mm）；

t_i——第i元件的厚度（mm）；

l_i——第i元件的长度（mm）；

R_c——垫圈重心半径（mm）；

R_n——在（第n点）接头处接触表面的平均半径（mm）。

将零件分割成许多组合元件，标出作用在它们上面的压力、作用力和力矩。例如图4-14上的楔式闸阀阀体，用字母a，b，d等标出重合截面，我们可以写出两个邻接元件公共连接截面上的下列联立位移方程：

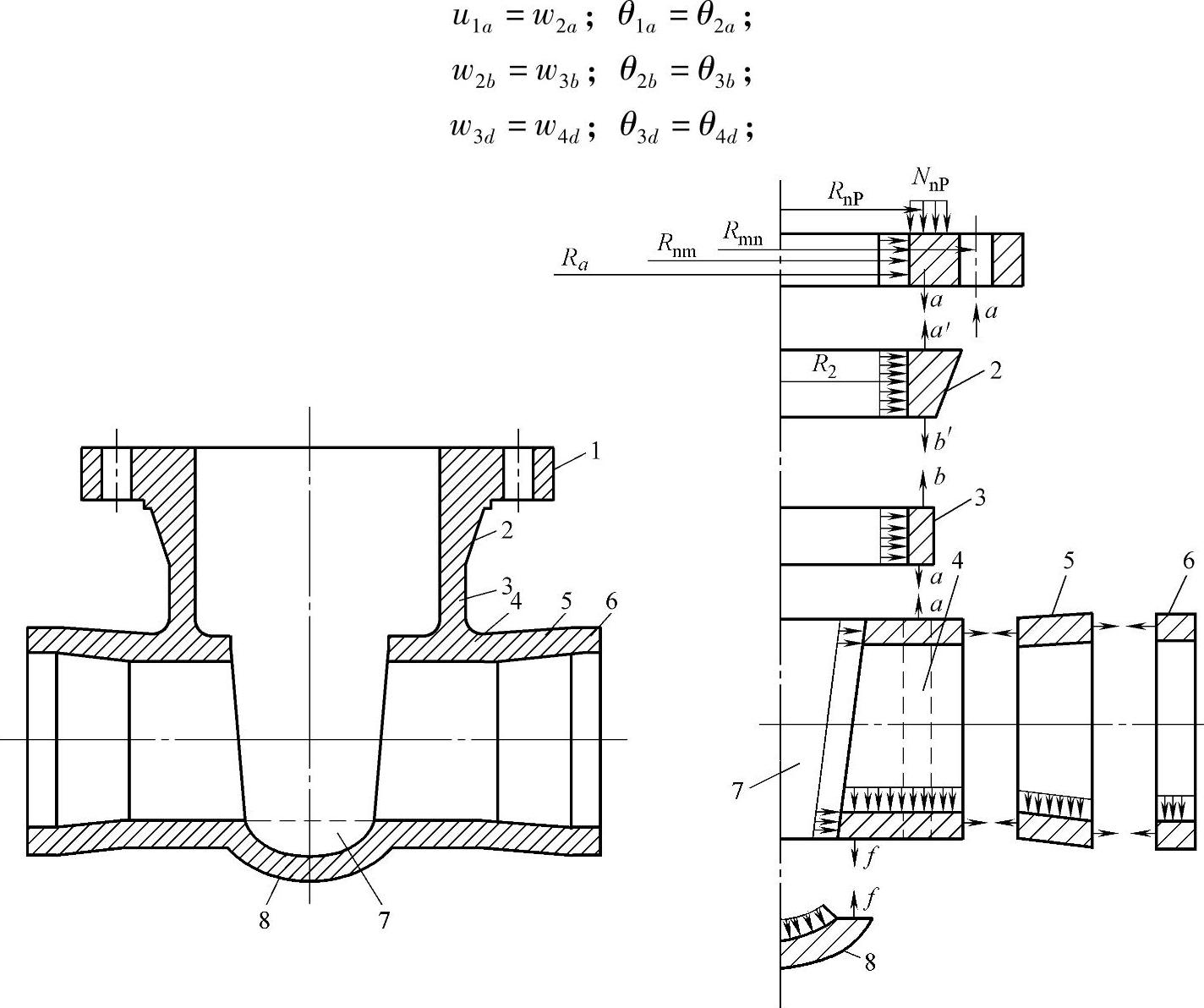
图4-14 收缩型浇注闸阀阀体的计算元件

1—组成法兰的平面环 2—厚度线性变化的圆柱形壳体（法兰与阀体的过渡段） 3—形成楔块移动内腔的圆柱形壳体 4—变长度的圆柱形壳体，在其中放置供阀体密封圈用的套筒 5—等壁厚的锥形壳体，由公称通径向密封直径的过渡段 6—圆柱形壳体，形成供阀体与管道焊接用的套筒 7—不闭合圆柱形壳体，与元件4相连，其轴线垂直于壳体的轴线 8—球形（或椭圆形）壳体

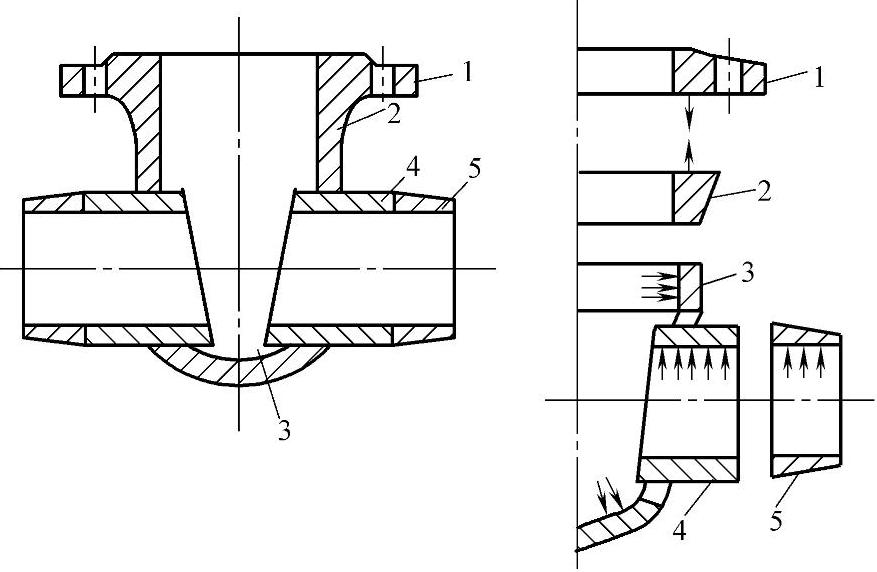
图4-15 全径直通式楔形闸阀焊接阀体的计算元件

1—平面环 2—厚度线性变化的圆柱形壳体（圆环） 3—球形壳体，在它的一个轴线上开了两个孔以供直通套筒用 4—圆柱形壳体 5—圆锥形壳体

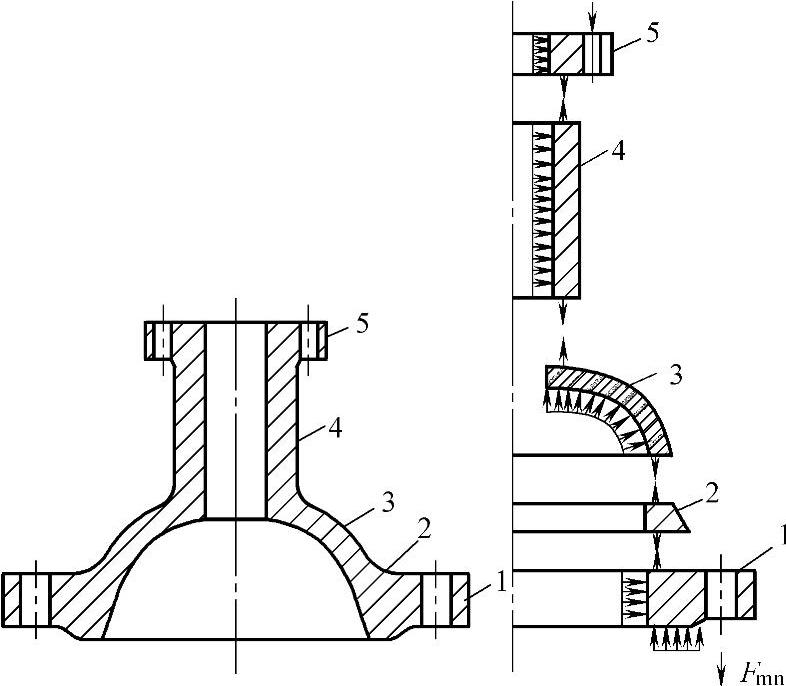
图4-16 楔形闸阀圆形阀体的高阀盖计算元件

1—平面环 2—厚度线性变化的圆柱形壳体（圆环） 3—球形壳体 4—圆柱形壳体，它形成填料函外壳和供固定压盖法兰用的支座 5—平面环（固定压盖或框架的法兰）

阀体是在阀门开启并处于压力的条件下进行研究的。在阀杆上没有作用力。作用在元件1上的有介质压力p₁、垫片作用力N_np、螺栓拉紧力F_mn、轴向力N₁和力矩M₁。单个元件2的反作用力和可能作用在法兰上的横向力H₁。如果能满足0.5＜l₁/S₁＜1.2的条件，元件可当作圆环来看待。

螺栓拉紧力F_mn换算成垫片平均圆周上的单位长度上的作用力。因螺栓拉紧作用沿螺栓周界每mm上应有的单位长度力为

N_mn=F_mn/（2πR_mn）

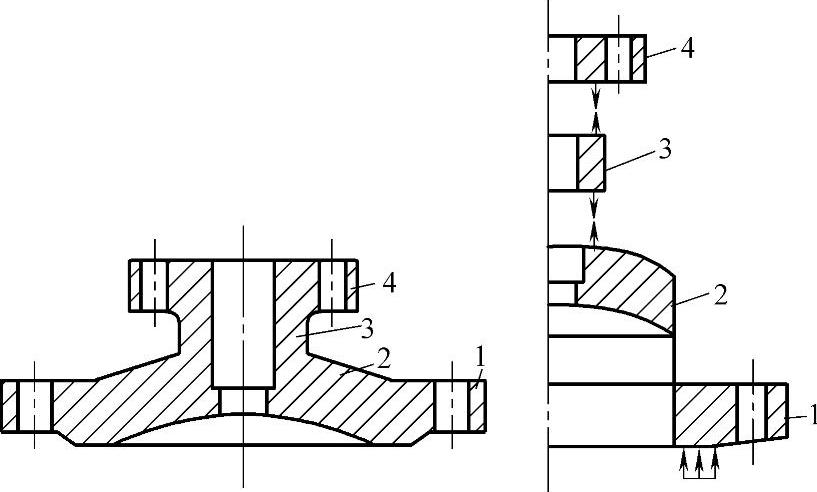
图4-17 楔形闸阀圆形阀体的阀盖计算元件

1—平面法兰环 2—球形壳体 3—圆筒形腔体 4—支承框架的平面环

壳体开孔，壳孔面积上的介质压力作用而在半径为R₂的每1mm周界上所具有的单位长度纵向力为

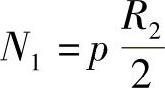
在半径为R_mn的圆周上每1mm长应具有的单位长度外力（阀盖通过垫片作用于阀体）N_np为

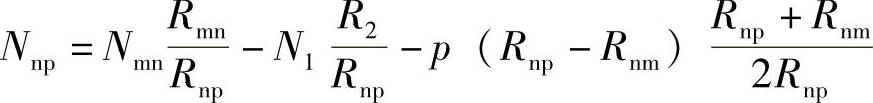
如果能满足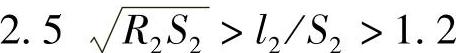条件的话，元件2可看作短圆柱形壳体。当l₂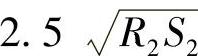＞时，壳体可视为半无穷长壳体。如果形成的圆柱各边具有不同的长度（斜切口），则采用

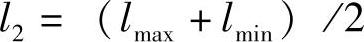
作用于圆柱上端面的作用力须换算成壳体平均半径R₂上的作用力

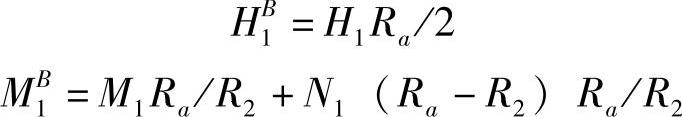
元件上端面的位移

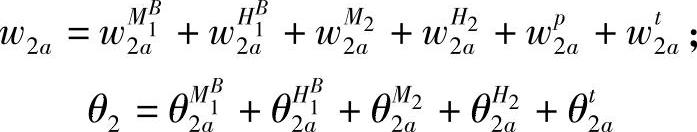
其他元件也按同样的顺序进行研究。由于阀体轴向不对称，所以在解决元件7的强度时，计算上会遇到困难，它不能用板壳理论的经典方法来解决，因此计算阀体主截面的强度时采用近似的方法。此法把钢的可塑性考虑进去了，这在一定程度上会展平截面上的应力。在“标准”给出确定应力系数的修正系数。当查明作用于每个零件元件上的作用力和力矩以及符合元件变形的条件后，要根据元件的厚度与线性尺寸的比值把元件分成薄壁和厚壁，再用不同的公式计算它们的强度。应用“标准”中给出的为计算确定和实验确定应力、应变、位移和作用力的通用方法。

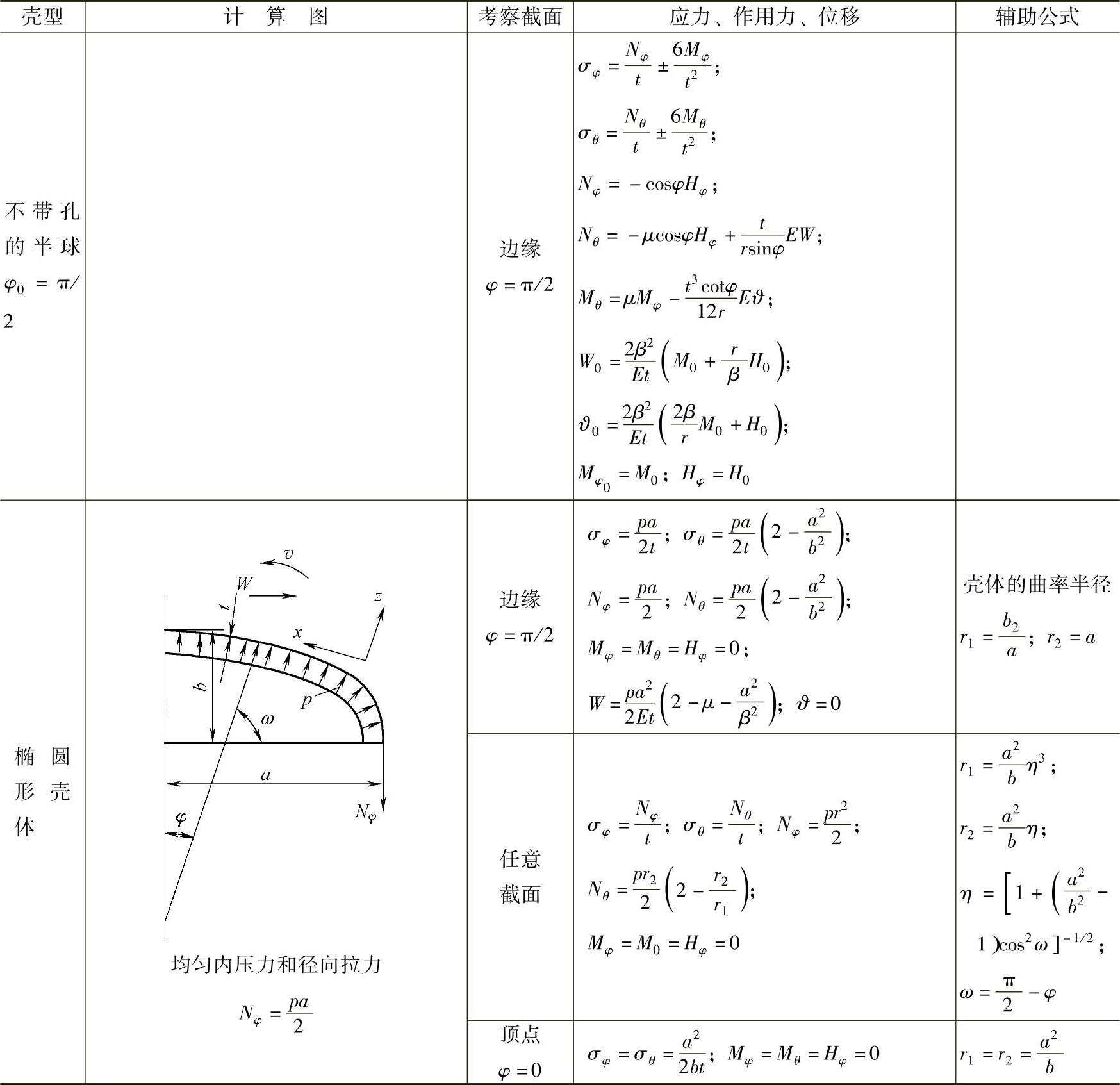
在表4-18中给出了因由内压所产生的负荷下，某些被推荐的公式在表中也给出了为设计阀门所采用的某些条件。

在计算壳体的图形中和公式中采用下列符号：

r——平均半径（中间表面的半径）（mm）；

t——壳体的厚度（mm）；

l——圆柱形短壳的长度（mm）；

z——圆筒轴线到边缘的距离（mm）；

φ——在球形壳体的子午面上，从转轴算起到要求的截面的角度（rad）；

φ₁——顶部有孔的球形壳体“底部”边缘角（rad）；

w——垂直于转轴的径向位移（mm）；

θ——与子午线相切的转角（rad）；

M_φ、M_θ——径向和环向单位长度上的弯矩（N·mm）/mm；

N_φ、N_θ——径向和环向单位长度上的拉（压）力（N/mm）；

H_φ——作用于平行圆环平面上单位长度上的剪切力（N/mm）；

σ_φ、σ_o——径向和环向应力（MPa）；

E——纵向弹性模量（MPa）；

μ——泊桑系数；

α——温度线胀系数（1/℃）；

D=Et³/[12（1-μ²）]——圆筒的刚度（N/mm）。

对于圆柱形壳体，脚标φ用z来替代。

表4-18 在内压和轴对称边缘力作用下，确定等厚薄壁壳体上的应力、作用力和应变的公式

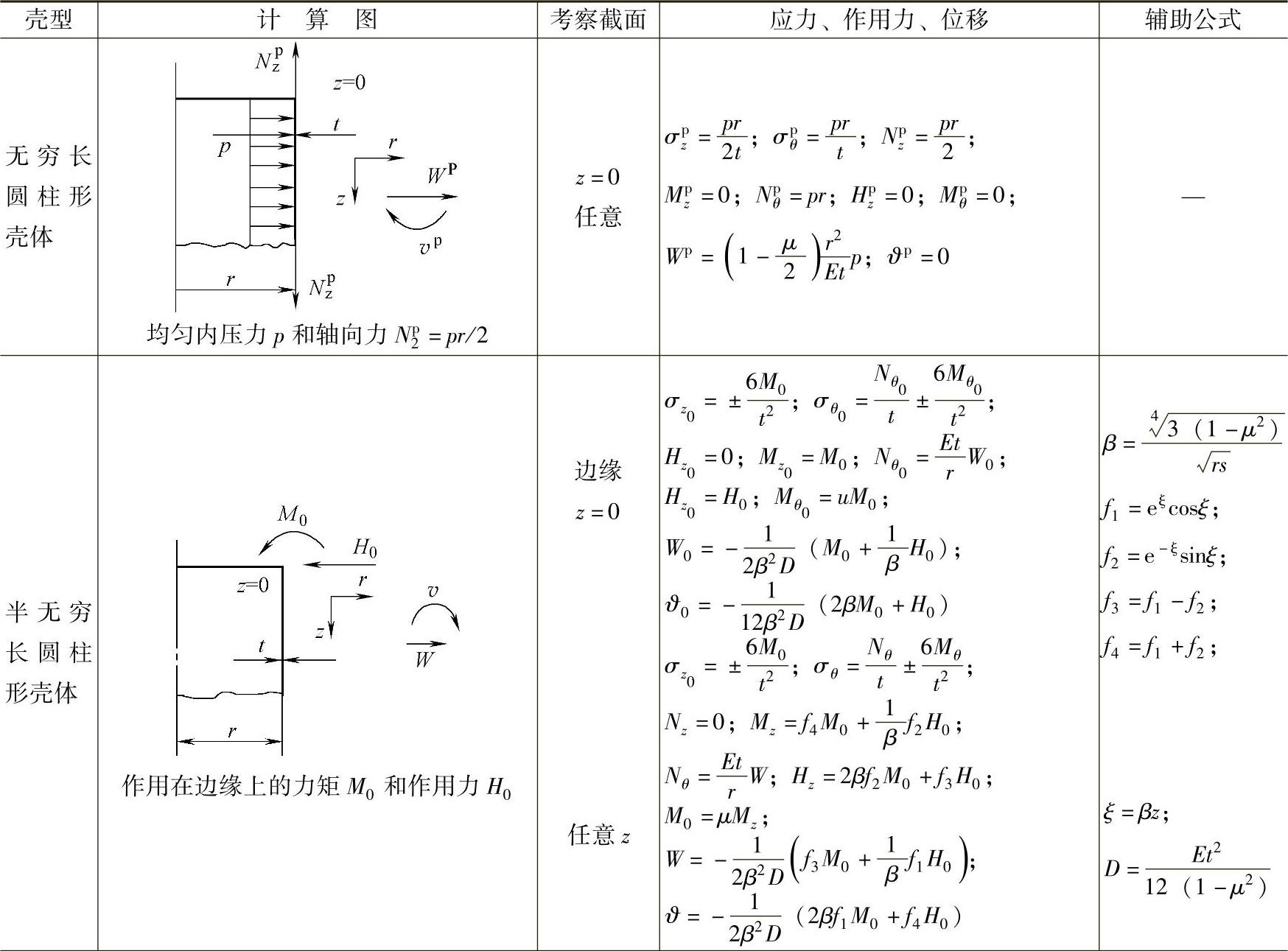
（续）

（续）

所要研究的元件和结构都是沿轴向对称的，而且载荷是在弹性变形限度内起作用，后一个条件在阀门上总是存在的。应力、位移和作用力是通过外部载荷而表现出来的。当几种载荷同时作用时，应力、位移和作用力是利用叠加法来确定的。应变可根据胡克定律，即应变和应力之间的线性关系来确定。计算时应遵守应力、应变、位移和作用力的符号定则，采用下列计算坐标系：

1）旋转薄壁壳体采用局部、右手、直角坐标系，坐标轴的方向为沿子午线的切线方向、平行圆环的切线方向以及沿薄壳中面的外法线方向。

2）轴对称的薄板采用圆柱坐标系

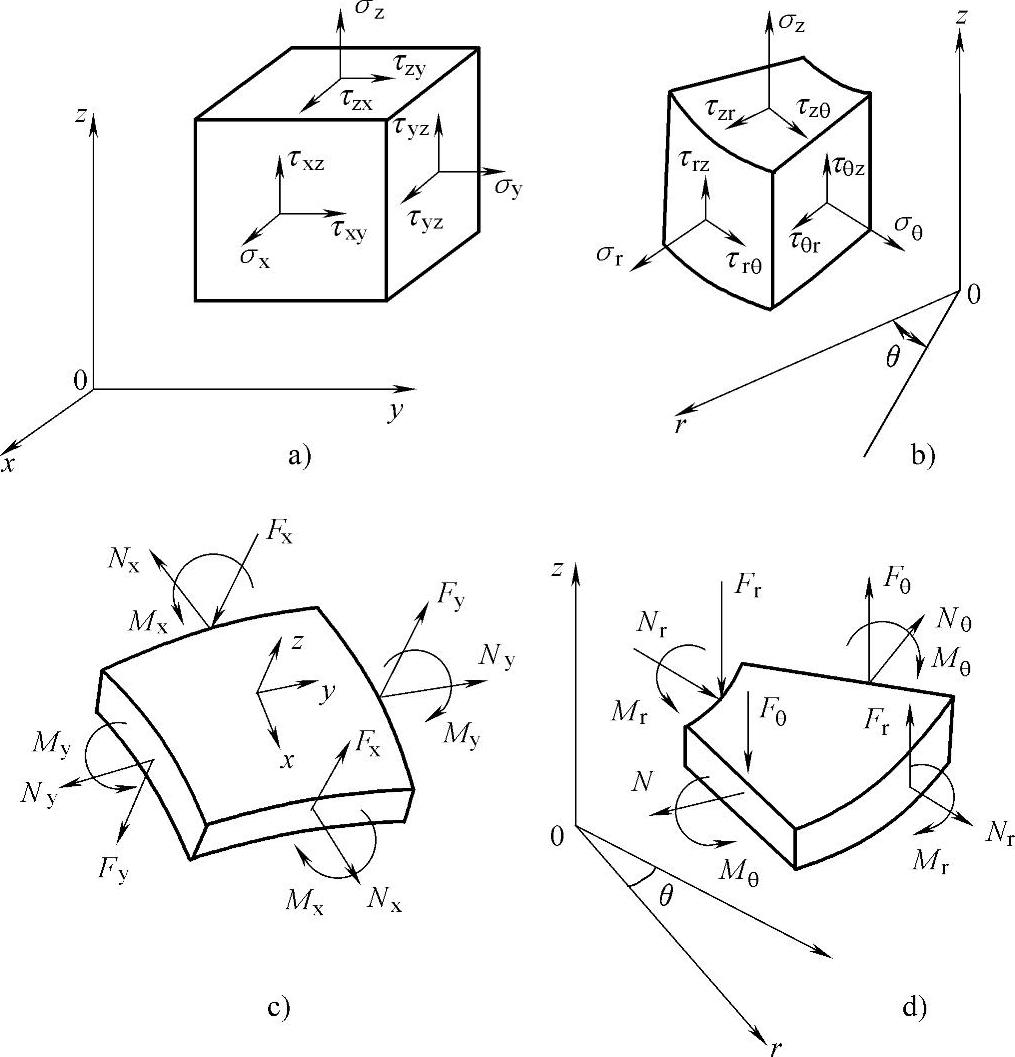
当我们研究由薄壳、薄板和圆环组成的结构时，可以采用其中一种坐标系和薄壳符号定则或薄板符号定则。当应力、应变、位移和作用力作用在所选用的坐标轴方向上时，使用下列符号定则：如果与坐标轴的正方向相符，则线性位移为正，如果相对于轴的旋转用螺旋定则与这些轴的正方向相一致的话，则认为它们为正。如果法向应力的方向与它们作用的面上的外法线方向相符的话，则法向应力为正（拉伸时），如图4-18所示。如果切应力的方向如图4-18上所示，则切应力为正。纵向拉伸应变假定为正，由正切应力产生的切应变假定为正。静态等效于作用在薄壳或平板正截面（相对于坐标轴而言）上应力的法向力和横向力与弯矩，如果它们方向如图4-18c、d上所示那样，则认为是正。

(www.xing528.com)

图4-18 符号定则

a）笛卡尔坐标系上应力的正方向 b）圆柱坐标系上应力的正方向 c）在壳内法向力和横向力以及弯矩的正方向 d）在平板内法向力和横向力以及弯矩的正方向

在图4-19上示出了在薄壳的子午线平面上，当沿着子午线移动坐标读数的不同方向上，位移W、U、转角θ、作用力F、N和弯矩M的正方向。当沿子午线移动坐标读数的方向改变时，θ、U和F的正方向则变成负方向。在计算中当某个值得到负值时，这表明它的方向与所取的方向相反了。在壳体应力的公式里所标出的符号（±）是表示壳体的外表面（+）和内表面（-）。当改变法线方向时，θ、M、F的正方向变成负方向。

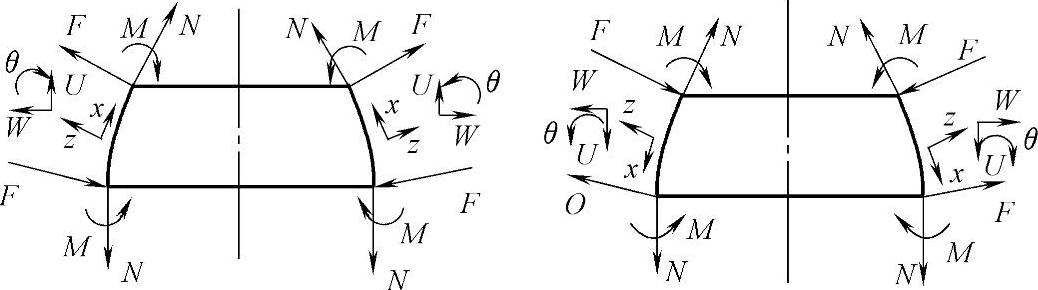
图4-19 沿薄壳子午线移动坐标系读数的不同方向上，位移 W、U，转角θ，作用力F、N和弯矩M的正方向

如果壳体壁厚与半径相比较很小时，可看作薄壳，则径向位移与壳体厚度相比很小。当增大t/r比值时，公式的误差也会增大。例如，当t/r≤0.05时，公式误差不超过5%，而当t/r≤0.1时，误差小于10%。如果壳体长度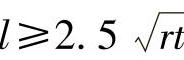时，可认为壳体为半无限长，否则在计算时应用矩形壳体公式。在壳体内的应力按下述公式确定：

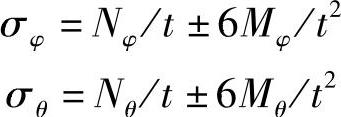
对于外侧用（+）号，而对于内侧用（-）号。对于壁厚和外半径的比值不超过0.2即t/r_map≤0.2的薄壁板，挠度与板壁厚度相比很小。平板内的应力按下列公式确定：

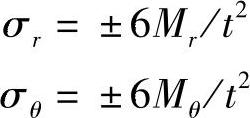
弯曲时的径向位移：

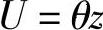
当几个载荷同时作用时，利用叠加的方法，这就是把载荷分解成分载荷，对于每种分载荷要单独进行计算，然后把每个分载荷的计算结果代数相加。

校核计算时，在有效应力与许用应力进行对比的基础上来评价强度。许用应力与零件材料、应力特点或类别以及所要研究的状况有关，状况包括正常的运行条件，正常运行条件的破坏或事故状况。已规定下列主要的应力类别：

总薄膜应力（σ）_m

局部薄膜应力（σ）_mn

总弯曲应力（σ）_n

局部弯曲应力（σ）_nn

总温度应力（σ）_t

局部温度应力（σ）_tn

薄膜补偿应力（σ）_Kn

扭转补偿应力（σ）_Kz

弯曲补偿应力（σ）_Kn

应力集中区内的局部应力（σ）_nK

在计算标准上给出下列典型的应力分类：

（1）薄膜应力 沿圆柱形或球形壳体的壁厚，由内压或外压作用引起的平均拉应力或压应力，以及在螺栓或双头螺柱的截面上的平均应力称为薄膜应力。

（2）局部薄膜应力 在壳体与法兰连接的区域内的薄膜应力以及管接头与壳体连接区域内的薄膜应力。

（3）总弯曲应力 内压作用在平盖上所引起的弯曲应力以及在可拆卸连接的互搭和刚性法兰上的弯曲应力。

（4）局部弯曲应力 在不同壁厚的两个圆筒连接区域内及圆筒与封底连接区域内，由内压作用所引起的弯曲应力，以及在法兰与管道连接的区域内由拉应力作用引起的弯曲应力。

（5）总温度应力 在圆筒内由轴向温差所引起的应力：在不同温度场合的构件的连接区域内（法兰与容器的圆筒部分，管接头与容器的筒体、管道与法兰）的应力；不同材料制成的管道，其连接处的应力；沿平底或平盖的厚度因温度梯度引起的应力。

（6）局部温度应力 由温度梯度沿壳体圆筒部分的壁厚、盖和底的球形部分的壁厚引起的应力；在容器或管道的壁面上过热（或过冷）而在局部地方产生的应力；在抗腐蚀的内衬上，由母体材料和内衬材料不同的温度线胀系数引起的应力。

（7）补偿应力（薄膜补偿应力、弯曲补偿应力和扭转补偿应力） 由于管道温度自由膨胀受到限制而引起的，沿管道截面均匀分布的拉（或压）应力（薄膜补偿应力）；由管道自补偿所引起的在管子的弯管段上的弯曲应力和扭转应力（相应于弯曲补偿应力和扭转补偿应力）。这对角式阀门是现实存在的。

（8）应力集中区内的局部应力 在孔、凹槽、应力未消除的焊缝、螺纹等的区域内的应力。

阀门零件考虑分成一定的应力等级，计算时应力应确定下来，并与许用应力进行比较。由于阀体串联在管线上，因此，它是管线上的一个部件。特别要强调的是连接部件——与管道同一作用的法兰和管接头，它是阀门与管道共用的。

与此同时，阀门与一般的管道部件，如三通、过渡管、弯头等相比还有其本质的区别。阀门是一个复杂的压力管道元件，它设有机械机构和传动机构。很多阀门零件加工时要求有较高的精度和有Ra值较低的表面粗糙度。连接在管线上的阀体不允许有一点变形，以免破坏其密封性能。因此，在安装阀门时应规定有补偿节，以减小阀体上的轴向力，不致使阀体产生变形。

这样，对被检查回路上工作的受压容器提出的全部要求，以及对管道提出的绝大部分要求，除了某些与阀门的功用不相符的以外，都适用于阀门。这些状况在完成阀门的验证计算中应予以考虑。

将阀体当作受压容器计算时，应计算下列应力组合：

总薄膜应力（σ）_m；

折合应力（σ）₂。它是由总薄膜应力或局部薄膜应力的分量和总弯曲应力的分量之和来确定；

折合应力范围（σ）_R1。它是由总薄膜应力或局部薄膜应力的分量，总弯曲应力和局部弯曲应力的分量以及总温度应力的分量之和来确定；

折合应力幅度（σ_a）1。它是由总薄膜应力或局部薄膜应力的分量、总弯曲应力和局部弯曲应力的分量及因应力集中而产生的总温度应力和局部温度应力的分量之和来确定。

当计算管道时应计算总薄膜应力（σ）_m和折合应力（σ）_s。它是由总薄膜应力或局部薄膜应力的分量、（薄膜、扭转和弯曲）补偿应力的分量以及总弯曲应力的分量之和来确定。折合应力范围（σ）_R是由总薄膜应力或局部薄膜应力的分量、（薄膜、扭转或弯曲）补偿应力的分量、总弯曲应力或局部弯曲应力的分量以及总温度应力的分量之和来确定。折合应力幅度（σ_a）2是根据总薄膜应力或局部弯曲应力，因应力集中而产生的总温度应力和局部温度应力的分量之和算出的。

当计算螺栓和双头螺柱时，应计算它们横截面上的平均应力（σ）_m1，它是由机械载荷引起的，规定称为薄膜应力。计算机械载荷和温度载荷引起的螺栓和双头螺柱上的平均应力（σ）_Bm1，计算由薄膜应力的分量、总弯曲应力和温度应力的分量以及扭转应力的分量之和来确定的折合应力（σ）₄。折合应力幅度（σ_a）₃由薄膜应力的分量、总弯曲应力的分量、扭转应力的分量以及考虑到应力集中而产生的温度应力的分量之和来确定。

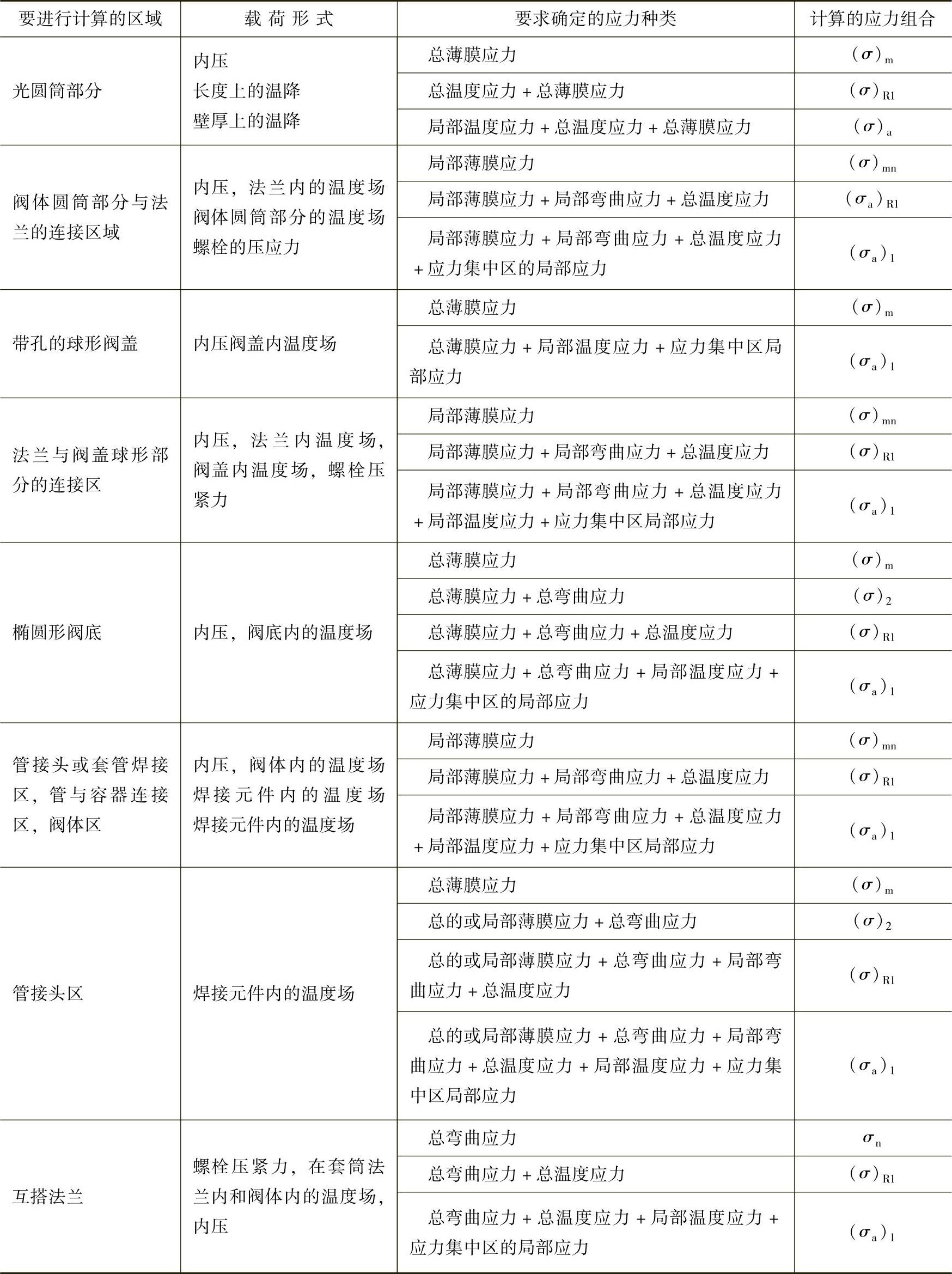
应按下列次序来确定：分析有效载荷和温度场，在此基础上选择零件（阀体和阀盖）最大应力区域，但是对于不同的计算条件，这个区域也可能各异。在表4-19上给出的区域是最典型的区域。

表4-19 阀体零件的某些区域内计算的应力组合

为了确定在要求计算的结构区域内各类应力的分量，从下列坐标系中选择一种：

带x、y、z坐标轴的直角坐标系；

带θ、r、z坐标轴的圆柱坐标系；

带θ、r、φ坐标轴的球坐标系。

坐标轴定在所要选择的方向上。法向应力和切向应力的分量分别以下列符号来表示：

在直角坐标系内：σ_x、σ_y、σ_z、τ_xy和τ_xz、τ_yz；

在圆柱坐标系内：σ_θ、σ_r、σ_z、τ_θr和τ_rz、τ_θz；

在球坐标系内：σ_θ、σ_r、σ_φ、τ_θr、τ_θφ和τ_rφ。

然后，根据每一种设计情况（拧紧螺栓、启动、稳定工况、事故保护系统投入工作、反应堆的工作改变、停堆、正常运行条件的破坏、事故工况）所获得的应力分量σ_x、σ_y、σ_z的总数，计算出主应力σ₁、σ₂、σ₃和折合应力（σ₁-σ₂）、（σ₂-σ₃）和（σ₁-σ₃）。确定一种计算组合应力：（σ）_m、（σ）_mn、（σ）₂、（σ）₃、（σ）₄。用折合应力的最大值与许用应力进行比较。

折合应力范围（σ）R1和（σ）R2按如下顺序计算：

1）首先确定需要研究的设计工况（如启动）下的主应力，规定用下角标i、j、k。

2）在确定主平面上建立应力σ_i、σ_j、σ_k的变化关系式，以供下面的计算使用。

3）对应于σ_imax、σ_imin、σ_jmax、σjmin、σkmax、σkmin值的不同时刻，确定其折合应力值。

4）当确定折合应力时，运用在第5）步上所列举的应力值和相应该时刻与其相应的其余两个主应力值，如σ_jmax和相应时刻的σ_i和σ_k；又如σ_imin以及相应时刻的σ_j和σ_k等。

5）条件折合应力按下列公式确定：

当τ=τ1时，，，，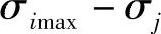

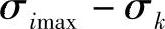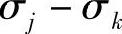当τ=τ2时，；；；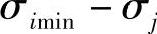

…………………………………………………

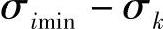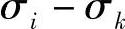当τ=τB时，；；；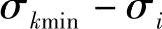

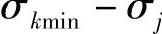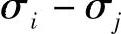式中 τ₁、τ₂、…、τ_B——相应的时刻。

折合应力值的计算顺序和上述一样保持不变，它与σ_i、σ_j、σ_k的代数值的比值无关，因此，它们既能采用正值，也能采用负值。

6）最后算出折合应力的最大值和最小值。

根据计算结果确定折合应力范围，它是取上列值中的最大值：

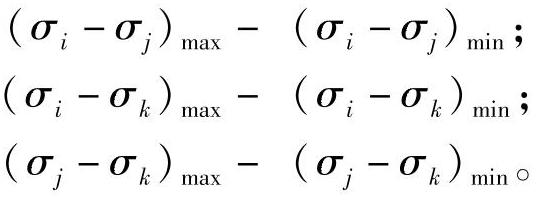
在所有情况下应力范围值应满足下列条件：

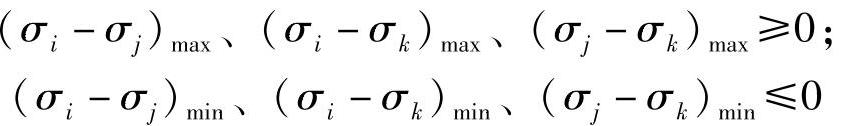
必须确信，与应力范围最大值相对应的时刻，就是挑选出σ_imax、σ_imin、σ_jmax、σ_jmin、σ_kmax、σ_kmin值的时刻。如果这个条件不能满足，就要对其他时刻进行计算。因此，必须确定当主应力对时间的导数等于零，即的那些时刻的应力范围。

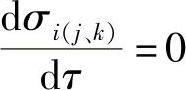
一般主平面位置在加载过程中不会改变。如果这个条件不能满足，应力随时间变化的过程可分解成相应于不同主平面位置的几个周期。每个周期可单独来研究。每一个主应力的下角标保持不变，而应力σ_i、σ_j、σ_k的变化与主平面的方位无关。

折合应力幅度的确定和应力范围的确定顺序一样，不同之处仅仅在于应力分量的总变化过程，它是考虑到应力集中系数而计算出来的，它可以分解成周期，在周期内主应力的值达到最大和最小（按一个周期）。因此，改变是从最大值到最小值以及从最小值到最大值，在每个加载周期内折合应力的幅度从下列三个公式中取其最大数：

疲劳断裂强度按条件折合弹性交变应力的幅度σ_a^∗来计算，σ_a^∗等于局部变形范围与计算温度下的弹性模量乘积的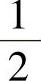。按照运行时所给定的应力幅度下的许用周期数或运行时所给定的周期数下的许用应力幅度来初步确定疲劳计算曲线—公称应力的许用幅度与许用周期数之间的关系曲线。最后的计算按照相应的公式进行。