法兰连接螺栓热变形与应力计算及强度分析

在温度t=20℃时，组装带螺栓的法兰连接时（图4-2）形成了弹性闭合尺寸——力链，在这种链上，螺栓的拉应力靠作用于其他零件上的压紧力来平衡。当介质的温度升高到工作温度之前，闭合链上的零件温度也升高。对于组成闭合链的每个元件，根据它距离工作介质的远近程度不同，而获得不同的l_p值（l_p为温升膨胀伸长量），由于组成弹性的尺寸——力链的零件被加热而变长，并随着拉伸和压缩元件热伸长之差，在螺栓上的作用力也跟着变化。如果闭合链的压缩部分的伸长超过拉伸部分（螺栓）的伸长，在螺栓上的作用力就会增大；如果螺栓的伸长超过压缩部分的伸长量，则作用力就会减小。

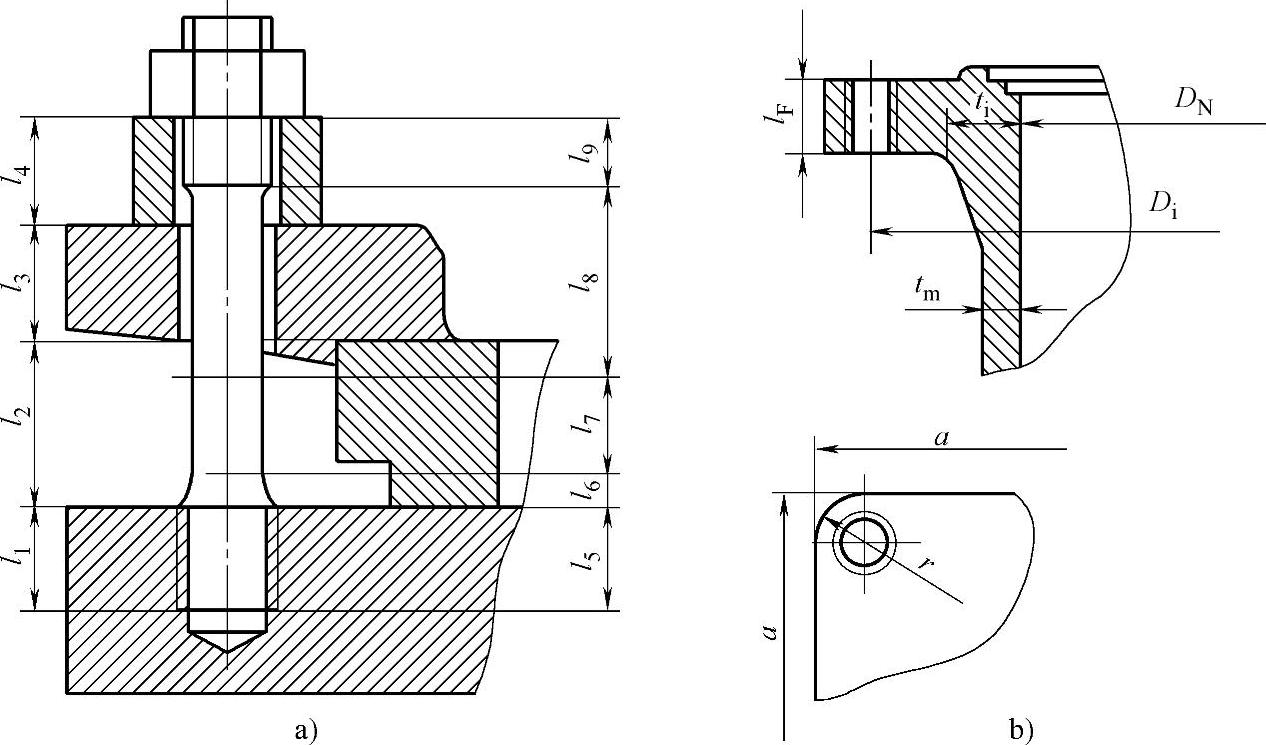
图4-2 法兰连接时确定螺栓上热应力的计算图

a）尺过链元件 b）法兰元件

螺栓上的附加热应力按下式来确定：

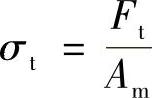
式中 σ_t——螺栓上的附加热应力（MPa）；

F_t——因温度而产生的附加作用力（MPa）；

A_m——螺栓的总横截面积（mm²）。

因温度产生的附加作用力F_t是由于尺寸链上的拉伸部分与压缩部分的伸长不同而产生的，并靠组成这个链的所有元件的弹性变形来补偿。因此，确定这种附加作用力的公式具有下列形式：

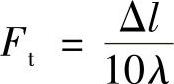
式中 Δl——尺寸链的拉伸部分与压缩部分的热伸长之差（mm）；

λ——链上所有元件的总柔度（mm/N）。热伸长之差

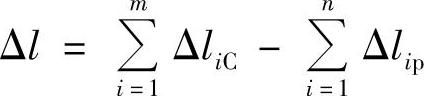
式中 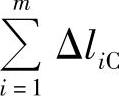——压缩元件的热伸长之和（mm）；

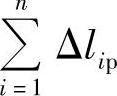——拉伸元件的热伸长之和（mm）；

m——压缩元件数；

n——拉伸元件数。

凡承受压缩或拉伸作用的零件或零件的一部分，并具有一定的计算加热温度的就算作元件。在现有的情况下，每个压缩零件就是一个独立元件，一个螺栓可看作由五个不同温度的元件组成，其中两个为螺纹元件，三个为圆柱元件，它们都工作于不同的条件下。

对于上述情况的具体计算公式：

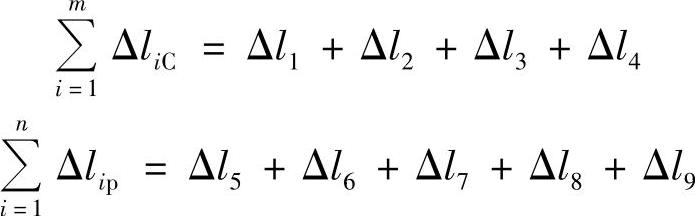
元件的热伸长按下式来确定：

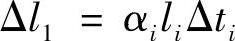(www.xing528.com)

式中 α_i——第i元件材料线膨胀系数（1/℃）；

l_i——第i元件的计算长度（mm）；

Δt_i——第i元件的温度比安装时的温度升高值（℃），Δt_i=t_i-20；

t_i——第i元件在工作条件下的温度（℃）。

链上所有元件的柔度系数总和按下式来确定：

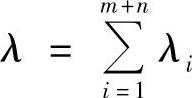
式中 λ_i——链上第i个元件的柔度系数（mm/N）。

元件的柔度系数取决于它的结构、尺寸和材料。对于圆杆（螺柱）或环形杆（圆管）

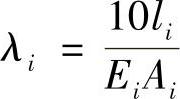
式中 A_i——第i元件的横截面积（mm²）；

E_i——第i元件材料的弹性模量（N/mm²）。

矩形法兰的柔度，如图4-2b所示，按下式计算：

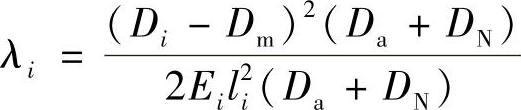
式中 D_m=D_N+2t（mm）；

t=0.5（t_m+t_i）（mm）；

D_a=0.5（a+D_N+Zr）（mm）；

式中 a——矩形法兰的边长（mm）；

r——矩形法兰的圆角半径（mm）；

Z——圆角的数量。

阀杆的热变形和附加应力的计算是与法兰连接螺栓的热变形和附加作用力的计算步骤一样，其区别只在于闭合尺寸——力链有所不同，阀杆—阀瓣—阀座—阀杆螺母的链段处于压缩状态，而阀体零件链段处于拉伸状态，一般在没有碟形弹簧的链上，阀杆链段的柔度系数比阀体零件的柔度系数大很多。

当链上具有碟形弹簧时，闭合尺寸——力链的柔度系数主要取决于碟形弹簧的总柔度系数，而其余零件的柔度系数约为碟形弹簧的（4～5）%，当阀门作近似计算时，可忽略刚性零件的柔度系数。